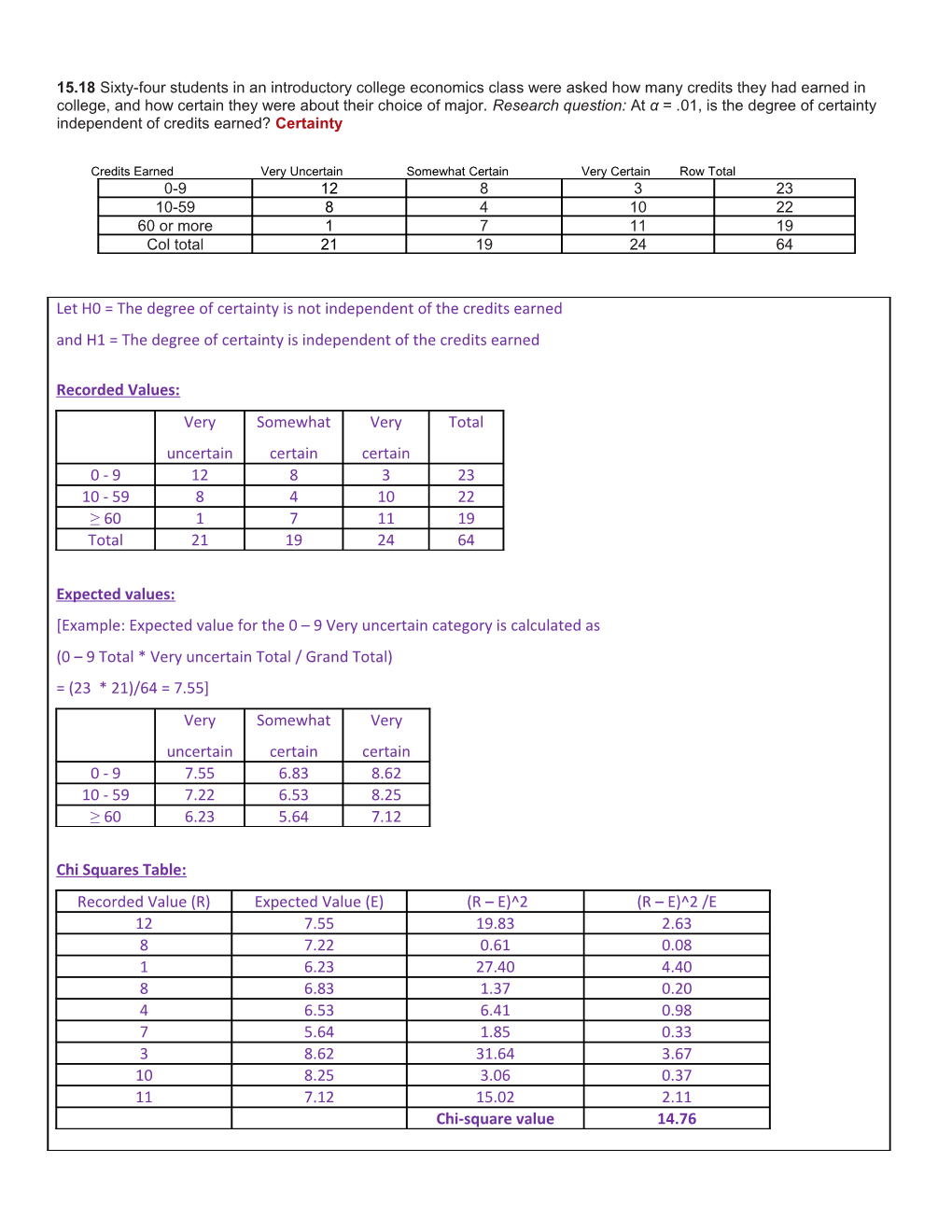
Credits Earned Very Uncertain Somewhat Certain Very Certain Row Total

15.18 Sixty-four students in an introductory college economics class were asked how many credits they had earned in college, and how certain they were about their choice of major. Research question: At α = .01, is the degree of certainty independent of credits earned? Certainty

Credits Earned Very Uncertain Somewhat Certain Very Certain Row Total 0-9 12 8 3 23 10-59 8 4 10 22 60 or more 1 7 11 19 Col total 21 19 24 64

Let H0 = The degree of certainty is not independent of the credits earned and H1 = The degree of certainty is independent of the credits earned

Recorded Values: Very Somewhat Very Total uncertain certain certain 0 - 9 12 8 3 23 10 - 59 8 4 10 22 ≥ 60 1 7 11 19 Total 21 19 24 64

Expected values: [Example: Expected value for the 0 – 9 Very uncertain category is calculated as (0 – 9 Total * Very uncertain Total / Grand Total) = (23 * 21)/64 = 7.55] Very Somewhat Very uncertain certain certain 0 - 9 7.55 6.83 8.62 10 - 59 7.22 6.53 8.25 ≥ 60 6.23 5.64 7.12

Chi Squares Table: Recorded Value (R) Expected Value (E) (R – E)^2 (R – E)^2 /E 12 7.55 19.83 2.63 8 7.22 0.61 0.08 1 6.23 27.40 4.40 8 6.83 1.37 0.20 4 6.53 6.41 0.98 7 5.64 1.85 0.33 3 8.62 31.64 3.67 10 8.25 3.06 0.37 11 7.12 15.02 2.11 Chi-square value 14.76 dof = (3 – 1)(3 – 1) = 4 For chi-square = 14.76 and dof = 4, the p- value is 0.0052 Since 0.0052 < 0.01, we reject the null hypothesis and accept Ha. Statistical evidence shows that the degree of certainty is independent of the credits earned.

15.22 A student team examined parked cars in four different suburban shopping malls. One hundred vehicles were examined in each location. Research question: At α = .05, does vehicle type vary by mall location? (Data are from a project by MBA students Steve Bennett, Alicia Morais, Steve Olson, and Greg Corda.) Vehicles

Vehicle Type Somerset Oakland Great Lakes Jamestown Row Total Car 44 49 36 64 193 Minivan 21 15 18 13 67 Full-sized Van 2 3 3 2 10 SUV 19 27 26 12 84 Truck 14 6 17 9 46 Col Total 100 100 100 100 400

Let H0 = The vehicle type is independent of the mall location and H1 = The vehicle type is dependent on the mall location

Recorded Values: Somerset Oakland GreatLake Jamestown Total Car 44 49 36 64 193 Mini van 21 15 18 13 67 Full size 10 2 3 3 2 van SUV 19 27 26 12 84 Truck 14 6 17 9 46 Total 100 100 100 100 400

Expected values: [Example: Expected value for the Car – Somerset category is calculated as (Car Total * Somerset Total / Grand Total) = (193 * 100)/400 = 48.25] Somerset Oakland Great Lake Jamestown Car 48.25 48.25 48.25 48.25 Mini van 16.75 16.75 16.75 16.75 Full size 2.5 2.5 2.5 2.5 van SUV 21 21 21 21 Truck 11.5 11.5 11.5 11.5 Chi Squares Table: Recorded Value (R) Expected Value (E) (R – E)^2 (R – E)^2 /E 44 48.25 18.06 0.37 21 16.75 18.06 1.08 2 2.5 0.25 0.10 19 21 4 0.19 14 11.5 6.25 0.54 49 48.25 0.5625 0.01 15 16.75 3.06 0.18 3 2.5 0.25 0.10 27 21 36 1.71 6 11.5 30.25 2.63 36 48.25 150.06 3.11 18 16.75 1.56 0.09 3 2.5 0.25 0.10 26 21 25 1.19 17 11.5 5.5 2.63 64 48.25 248.06 5.14 13 16.75 14.06 0.84 2 2.5 0.25 0.10 12 21 81 3.86 9 11.5 6.25 0.54 Chi-square value = 24.51

The p- value for chi square = 24.51 and dof = (5 – 1)(4 – 1) = 12 is 0.017 Since the p- value is lesser than  , we reject the null hypothesis and accept Ha. Statistical evidence shows that the vehicle type is dependent on the mall location.

15.24 High levels of cockpit noise in an aircraft can damage the hearing of pilots who are exposed to this hazard for many hours. A Boeing 727 co-pilot collected 61 noise observations using a handheld sound meter. Noise level is defined as “Low” (under 88 decibels), “Medium” (88 to 91 decibels), or “High” (92 decibels or more). There are three flight phases (Climb, Cruise, Descent). Research question: At α = .05, is the cockpit noise level independent of flight phase? (Data are from Capt. Robert E. Hartl, retired.) Noise

Noise Level Climb Cruise Descent Row Total Low 6 2 6 14 Medium 18 3 8 29 High 1 3 14 18 Col Total 25 8 28 61 Let H0 = The noise level is independent of the phase of flight and H1 = The noise level is dependent on the phase of flight Recorded Values: Climb Cruise Descent Total Low 6 2 6 14 Medium 18 3 8 29 High 1 3 14 18 Total 25 8 28 61

Expected values: [Example: Expected value for the Low-Climb category is calculated as (Low Total * Climb Total / Grand Total) = (14 * 25)/61 = 5.74] Climb Cruise Descent Low 5.74 1.84 6.43

Medium 11.89 3.80 13.31 High 7.38 2.36 8.26

Chi Squares Table: Recorded Value (R) Expected Value (E) (R – E)^2 (R – E)^2 /E 6 5.74 0.069 0.012 18 11.89 37.390 3.146 1 7.38 40.667 5.513 2 1.84 0.0269 0.015 3 3.80 0.645 0.170 3 2.36 0.409 0.173 6 6.43 0.182 0.028 8 13.31 28.212 2.119 14 8.26 32.921 3.984 Chi-square value 15.16

The p- value for chi square = 15.16 and dof = (3 – 1)(2 – 1) = 4 is 0.0044 Since the p- value is lesser than  , we reject the null hypothesis and accept the Ha. Statistical evidence shows that the cockpit noise level is dependent on the phase of flight.

15.28 Can people really identify their favorite brand of cola? Volunteers tasted Coca-Cola Classic, Pepsi, Diet Coke, and Diet Pepsi, with the results shown below. Research question: At α = .05, is the correctness of the prediction different for the two types of cola drinkers? Could you identify your favorite brand in this kind of test? Since it is a 2 × 2 table, try also a two-tailed two-sample z test for π1 = π2 (see Chapter 10) and verify that z2 is the same as your chi-square statistic.Which test do you prefer? Why? (Data are from Consumer Reports 56, no. 8 [August 1991], p. 519.) Cola Correct? Regular Cola Diet Cola Row Total Yes, got it right 7 7 14 No, got it wrong 12 20 32 Col Total 19 27 46

Chi-square Test: Let H0 = The correctness of prediction is independent of the cola type and H1 = The correctness of prediction depends upon the cola type

Recorded Values: Regular Cola Diet Cola Total Yes, got it 14 7 7 right No, got it 32 12 20 wrong Total 19 27 46

Expected values: [Example: Expected value for the Yes, got it right – Regular cola category is calculated as (Yes, got it right Total * Regular cola Total / Grand Total) = (14 * 19)/46 = 5.783] Regular Cola Diet Cola Yes, got it 5.78 8.22 right No, got it 13.22 18.78 wrong

Chi Squares Table: Recorded Value (R) Expected Value (E) (R – E)^2 (R – E)^2 /E 7 5.78 1.488 0.258 12 13.22 1.488 0.112 7 8.22 1.488 0.181 20 18.78 1.488 0.079 Chi-square value 0.63 The p- value for chi square = 0.63 and dof = (2 – 1)(2 – 1) = 1 is 0.427 Since 0.427 > 0.05, we fail to reject the null hypothesis. There is no statistical evidence to suggest that the correctness of prediction is not independent of the cola type.

Two-tail z- Test: H0: There is no difference between the abilities to identify the colas; that is, the correctness of prediction is independent of the cola type; that is, p1 – p2 = 0 Ha: There is a difference between the abilities to identify the colas; that is, the correctness of prediction depends upon the cola type; that is, p1 – p2 ≠ 0 n1 = 19, n2 = 27, p1 = 7/19 = 0.368, p2 = 7/27 = 0.259 p’ = (n1p1 + n2p2)/(n1 + n2) = (7 + 7)/46 = 0.304 q’ = 1 – p’ = 0.696 SE = Ö(p’q’) * Ö [(n1 + n2)/(n1n2)] = Ö(0.304 * 0.696) * Ö[46/(19 * 27)] = 0.138 z = (p1 – p2)/SE = (0.368 – 0.259)/0.138 = 0.791 [Note that z^2 = 0.791^2 = 0.626  The value of chi-square.] The two-tail p- value for z = 0.791 is 0.457 Since 0.457 > 0.05, we fail to reject the null hypothesis. There is no statistical evidence to suggest that the correctness of prediction is dependent on the cola type. The chi-square test appears to better since it is a general test for this type of questions. (Also note that 0.427 < 0.457)