Pre-Lab: Electric Fields s3

Phy 123L Mostly Review Name: ______Significant Digits, Unit Conversions, Graphing and Uncertainties in Measurements ======Choose the best answer. (30 pts total)

1. Do the following calculation and express the result in scientific notation with the correct number of significant digits: 36.94 - 25.2 + 100.81 = ??? a. 112.55 b. 112.6 c. 1.1255 x 102 d. 1.126 x 102 e. 1.126 x 10-2

2. Express 3300 g/cm3 in kg/m3. a. 3.3 x 102 kg/m3 b. 3.3 x 109 kg/m3 c. 3.3 x 103 kg/m3 d. 3.3 x 106 kg/m3

3. When drawing a graph, it is best to draw it small, so it takes only a small part of the graph paper and the data points are crammed together. In physics, we like to maximize the error in our graphs and measurements and make things hard to read. a. True b. False

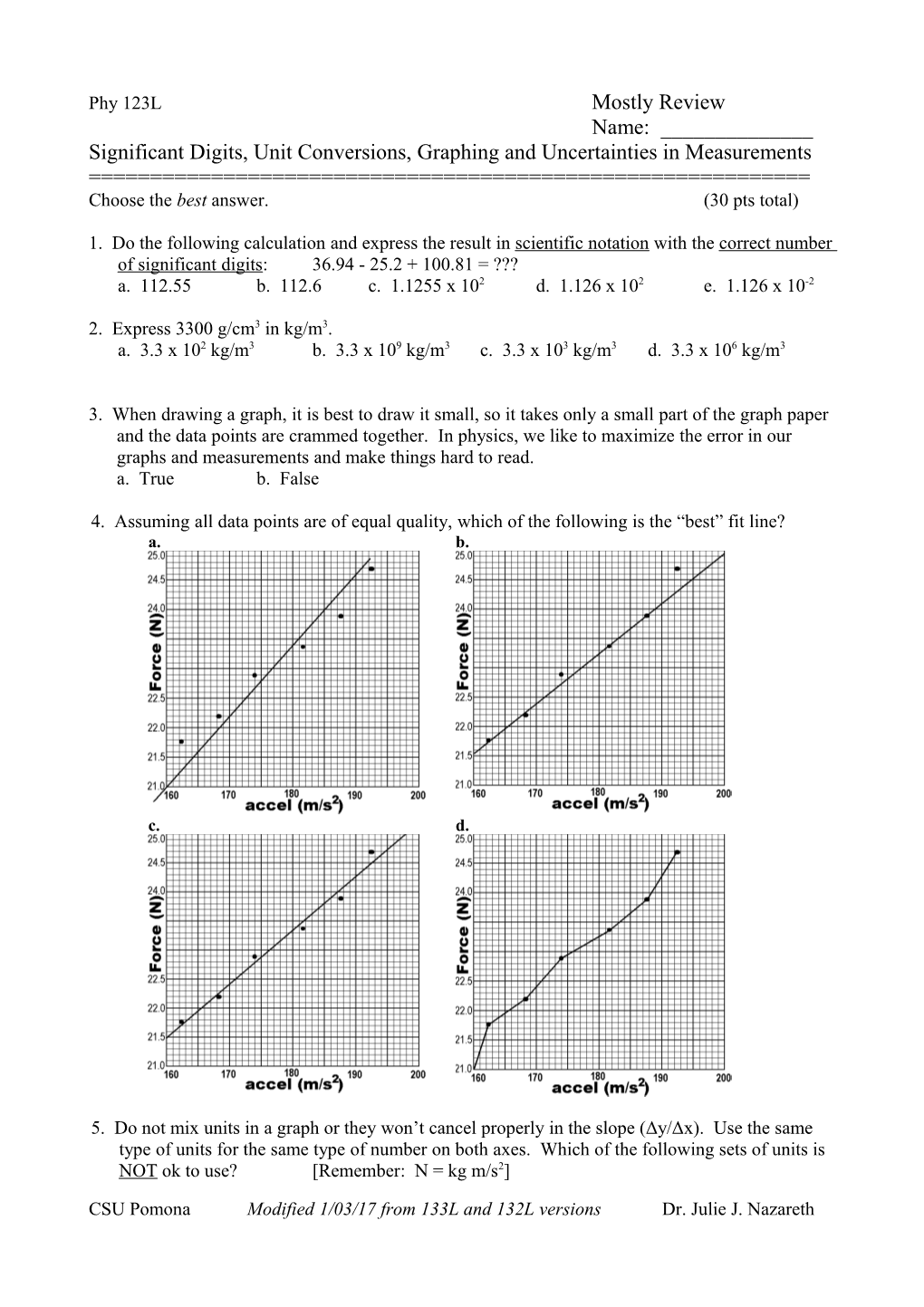
4. Assuming all data points are of equal quality, which of the following is the “best” fit line? a. b.

5. Do not mix units in a graph or they won’t cancel properly in the slope (Δy/Δx). Use the same type of units for the same type of number on both axes. Which of the following sets of units is NOT ok to use? [Remember: N = kg m/s2]

CSU Pomona Modified 1/03/17 from 133L and 132L versions Dr. Julie J. Nazareth Phy 123L Mostly Review a. y-axis = N and x-axis = m/s2 b. y-axis = g cm/s2 and x-axis = cm/s2 c. y-axis = N and and x-axis = cm/s2

6. When it is acceptable to use a data point as a slope point? a. if the data point appears to fall upon the line b. if the data point appears to fall upon the line and if it falls at the extreme end of the page c. NEVER, because this tends to influence the positioning of the “best” fit line.

7. To find the best possible value for the slope of a graph (while minimizing uncertainty), the two slope points should be (as much as reasonably possible) which of the following? a. at extreme ends of the page of paper c. at the intersection of the grid lines b. never a data point d. You want answers a, b and c

8. Which is the incorrect formula for calculating the slope (Δy/Δx) with the slope points (x1, y1) and (x2, y2)? a. (y1 – y2) / (x1 – x2) b. (y2 – y1) / (x2 – x1) c. (y1 – y2) / (x2 – x1)

9. How should you find the y-intercept of your graph? (Remember, choose the best answer.) a. Measure the y-value off your graph where the x-value is 0. b. Use the equation of a line to solve for the y-intercept algebraically. c. Answer b always works, but answer a works only if the graph includes the origin.

Questions 10-11: The data in your experiment is governed by the formula: A = (BC/D) – E You graph A on the “y” (vertical) axis and C on the “x” (horizontal) axis.

10. What is the slope theoretically equal to? a. B/D b. A/E c. –E d. C/A e. C/D

11. What is the y-intercept theoretically equal to? a. B/D b. E c. –E d. C/A e. C/D

Questions 12 and 15 refer to Uncertainty of Electronic Meters. Refer to the Appendix B table of your lab manual or ask your instructor for help. 12. A student measured a DC current using a Fluke 87III meter. What does the table in Appendix B show for the meter uncertainty? a. 0.05% + 1 digit b. 0.2% + 2 digits c. 1.0% + 2 digits d. 2.0% + 2 digits

Questions 13-15: A student measured an AC current of 0.152 Amps using a Fluke 8000A meter. The student knows that this meter has an uncertainty of 1.0% + 2 digits for AC current.

13. What is the least significant figure (LSF) in the student’s AC current measurement? a. 0 b. 1 c. 5 d. 2 14. What is the decimal place of the least significant figure (LSF) in the student’s AC current measurement? (You need to know this for the # digits part of meter uncertainty.) a. “tenths” place b. “hundredths” place c. “thousandths” place

15. What is the meter uncertainty of the current measurement in Amps? (Remember to round your final answer for uncertainty properly. See Do’s and Don’ts #26 for help or ask the instructor) a. .003 A b. .004 A c. .002 A d. .001 A e. .01 A CSU Pomona Modified 1/03/17 from 133L and 132L versions Dr. Julie J. Nazareth Phy 123L Mostly Review

Questions 16-17: You are using a ruler to measure lengths. Assume that you can reasonably measure to one-half of the smallest division. This means you can see if the length of the object is closer to one of the tick marks, half-way between two tick marks, or closer to the following tick mark. (If you can’t tell if a measurement is closer to a tick mark or half-way in between, then you can only reasonably measure to the nearest whole of the smallest division). This is your instrumental precision (instrumental uncertainty). 16. If the smallest division on your ruler is 1 mm (= 0.1 cm), what is the numerical value of your instrumental precision (instrumental uncertainty)? a. 1 mm b. 0.1 cm c. 0.05 cm d. 0.05 mm

17. If a rod is exactly three centimeters long, how would you record the length to reflect the precision of the instrument (and therefore, how well you can measure the length)? a. 30 mm b. 3.0 cm c. 3.00 cm d. 30.00 cm

Questions 18-19: A student made the following six measurements of the mass of an object: m = 56.6 g, 56.6 g, 56.6 g, 56.6 g, 56.6g, 56.6 g. The instrumental uncertainty is δinst = 0.1 g. 18. What is a reasonable estimate of the sample uncertainty, δsamp? a. 0.0 g b. 0.1 g c. 0.6 g d. 56.6 g

19. What is a reasonable estimate of the uncertainty of the measurement, δm? To determine this, look at both the instrumental and sample uncertainties and choose the larger value. a. 0.0 g b. 0.1 g c. 0.6 g d. 56.6 g

20. A student made the following nine measurements of the wavelength of a standing wave: l = 14.4 cm, 15.1 cm, 14.2 cm, 14.6 cm, 14.4 cm, 14.8 cm, 13.7 cm, 13.9 cm, 14.9 cm. Assume the instrumental uncertainty is 0.1 cm. What is a reasonable estimate of the sample uncertainty, δsamp? (Choose the best answer) a. 0.1 cm b. 0.4 cm c. 0.5 cm d. 0.7 cm e. 1 cm f. Answers c and d are both reasonable estimates.

21. A student measures a coefficient of linear expansion of (14.2 ± 0.8)x10-6 C°-1 for a steel tube and the accepted value for commercially available steel is 11.3 x10-6 C°-1 to 13.5x10-6 C°-1. How would you describe the two values/numbers? (Consider whether the ranges overlap.) a. They do not agree. (There is a significant discrepancy.) b. They are close but do not quite agree. (There is a slightly significant discrepancy.) c. They agree within uncertainty. (There is no significant discrepancy.)

CSU Pomona Modified 1/03/17 from 133L and 132L versions Dr. Julie J. Nazareth Phy 123L Mostly Review Questions 22 & 23: Propagating Uncertainty through a calculation Follow the outlined steps to perform the following calculations including uncertainty. Write out your final answer (value with its associated uncertainty) following the Rules for reporting experimental values (see Appendix C of the Phy 121L/131L lab manual). Reduce rounding error by keeping at least two extra non-significant digits in intermediate calculations. Show all work.

22. [(34.35 ± 0.05) g – (30.35 ± 0.05) g] (9.80 m/s2) = ??? Step 1: Subtract the values in the square brackets. Use Rule # 1: add absolute uncertainties. = [( ± ) g] (9.80 m/s2)

Step 2: Use Rule #4 to multiply the result in the square brackets by (9.80 m/s2), a “perfectly known number.” Remember, for Rule #4, multiply the absolute uncertainty by the “perfectly known number.” Don’t forget to also multiply the best estimate by the “perfectly known number”! = [( ± ) gm/s2]

Step 3 (Last step): Round the absolute uncertainty to one significant digit (or two SD if it the absolute uncertainty at the conclusion of the previous step begins with a “1” or a “2”) and round the equation result (best estimate) to the same decimal place. = [( ± ) gm/s2]

23. [(7.73 ± 0.01) cm] [(19.0 ± 0.1)mm]2 = ??? Give final answer in cm3. Step 1: Make both length measurements have the same units (mm → cm). Don’t forget to convert the absolute uncertainty also. = [(7.73 ± 0.01) cm] [( ± )cm]2

Step 2: Change the absolute uncertainties into relative uncertainties (as percentages) because you will need this for both the powers rule #3 (the square) and the multiplication rule #2.

= (7.73 cm ± %) [( cm ± %)]2

Step 3: Do the square. Square the best estimate and use Rule #3 to multiply the power (= 2 in this case) times the relative uncertainty. Don’t do anything to the 7.73 cm ± relative uncertainty yet. Just write it down in the calculation = (7.73 cm ± %) ( cm2 ± %)

Step 4: Multiply the best estimate numbers and use Rule #2 to add the relative uncertainties. = ( cm3 ± %).

Step 5: Change the relative uncertainty back to absolute uncertainty. = ( ± ) cm3

Step 6 (Last step): Round uncertainty to one significant digit (or two SD if it the absolute uncertainty at the conclusion of the previous step begins with a “1” or a “2”) and round the result of the calculation to the same decimal place. = ( ± ) cm3

CSU Pomona Modified 1/03/17 from 133L and 132L versions Dr. Julie J. Nazareth