SUPPLEMENTARY INFORMATION
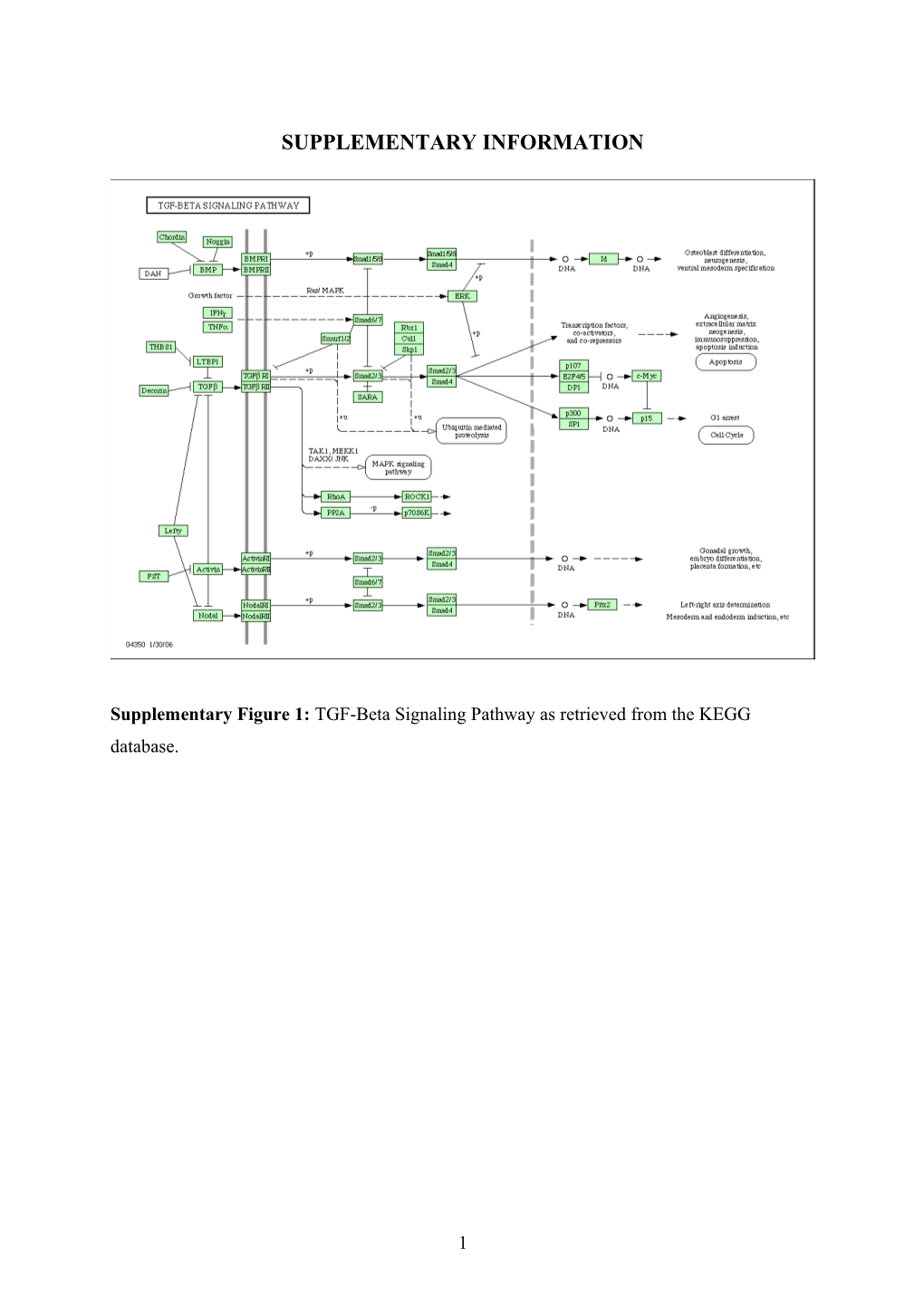
Supplementary Figure 1: TGF-Beta Signaling Pathway as retrieved from the KEGG database.
1 Supplementary Figure 2: DAG produced from TGF-Beta pathway map retrieved from the KEGG database. Each node is identified by gene symbol (e.g. DCN for Decorin). The remainder of this document is organized as follows:
Part I: lays out basic concepts required to follow BDe scoring function described in Secton 2.3
Part II: provides graph properties of the networks in KEGG database (which motivates the choice of synthetic networks) and configuration information about gold-standard Bayesian Networks (BNs - ALARM network and ASIA network) and synthetically generated 8 BNs to test the reliability of Bayesian Pathway Analysis (BPA).
Part III: shows the set of Conditional Probability Tables (CPTs) of BNs for ideal case and non-ideal case. An ideal case means data is generated according to consistent CPTs of the given BN under consideration. A non-ideal case means that a CPT is produced which is not consistent with independencies entailed by the DAG part of the BN.
Part IV: lists parameters of networks used in SynTReN to generate synthetic microarray data.
2 PART I: BAYESIAN DIRICHLET EQUIVALENT (BDe) SCORE CALCULATION
Given the gamma function note that . The beta density function with parameters and is defined as
We refer to this function as and a random variable F with this density function is said to have a beta distribution. One can show that
which yields . Suppose F has a beta distribution and X is a random variable with two values (1 and 2) such that , then . In a BN setting (without loss of generality, consider a binary BN), we view F as the “driving function” for node X, assign a prior set of parameters (a, b) for X and update the count for a and b, if there is some observed data.
Consider the single node binary BN to the left. Let’s consider X=1 to be heads and X=2 to be tails. If initially say, a=b=3, then we say probability of observing a heads is 3/6 = 1/2. Assume we use a biased coin and one now observes data d = 11112211111 with 9 1s and 2 2s. Then the distribution function is updated as a=3+9=12, and b=3+2=5 and we say probability of observing a heads is 12/17. If one has a valid reason to bias the initial configuration of a and b, this can be reflected in the prior distribution definition. For the above example, one could choose a larger value for a compared to b, initially.
Now consider binomial data d = (x1, x2, …, xM) with parameter F following and N= a+b. Assume we have s 1s and t 2s in d. One now can calculate =
For example, let a=b=1 and assume we observe d=(1,2), i.e. one heads and one tails. Then
Note that if a random variable X2 in a BN has a parent X1, then we would have two “driving functions” for X2, one for each instance of X1 (whether X1 is 1 or 2). Similarly, if a node in a BN has 2 parents, we would have four beta functions, one for each configuration of the values the node’s parents assumes (11, 12, 21, 22), and so on.
3 In Section 2.3 of the manuscript, we use Bayesian Dirichlet equivalent (BDe) scoring scheme, which uses Dirichlet functions driving each node, which is a generalization of the beta distribution. Based on the definitions listed here, first, let’s review the BDe score definition:
N qi (N ) ri (a s ) P(Data | Model) ij ijk ijk i1 j1 (Nij M ij ) k 1 (aijk ) where N is the number of nodes, qi is the number of different states of node’s parents, and ri is the set of values a node can take on. Nij is the sum of corresponding Dirichlet distribution hyper-parameters aijk. Mij is the number of times that the parents of node i take on configuration j in the dataset. Of these Mij cases, sijk is the total number of times in the sample that node i is observed to have value k when its parents take on configuration j.
Parameters used in this equation are best explained by an example. Consider the BN where nodes can take on values 1, 2, or 3 and follow Dirichlet distributions.
Note that X3 has two parents and since each node can take on 3 values, X3’s parents can take on 9 (3x3) different configurations. Following equivalent sample size method, sum of the initial Dirichlet hyper-parameters, aijk, driving each node has the same total, 27. Hence,
a111 = a112 = a113 = a211 = a212 = a213 = 3, and a311 = a312 = a313 = 1 (X3’s parents take on configuration 1, i.e. X1=1, X2=1) a321 = a322 = a323 = 1 (X3’s parents take on configuration 2, i.e. X1=1, X2=2)
4 a331 = a332 = a333 = 1 (X3’s parents take on configuration 3, i.e. X1=1, X2=3) a341 = a342 = a343 = 1 (X3’s parents take on configuration 4, i.e. X1=2, X2=1) a351 = a352 = a353 = 1 (X3’s parents take on configuration 5, i.e. X1=2, X2=2) a361 = a362 = a363 = 1 (X3’s parents take on configuration 6, i.e. X1=2, X2=3) a371 = a372 = a373 = 1 (X3’s parents take on configuration 7, i.e. X1=3, X2=1) a381 = a382 = a383 = 1 (X3’s parents take on configuration 8, i.e. X1=3, X2=2) a391 = a392 = a393 = 1 (X3’s parents take on configuration 9, i.e. X1=3, X2=3)
Now, let’s consider a sample input data and focus on node 3:
Observation X1 X2 X3 1 3 1 2 2 3 1 1 3 1 2 1 4 2 1 3 5 2 2 1 6 1 3 2 7 1 3 3 8 3 3 2 9 3 2 3 10 2 3 1
Note that N31 = N32 = N33 = N34 = N35 = N36 = N37 = N38 = N39 = 3.
Considering observed data,
M31 = 0, M32 = 1, M33 = 2, M34 = 1, M35 = 1, M36 = 1, M37 = 2, M38 = 1, M39 = 1.
rd That is, for example, M37 = 2 means 3 node’s (X3’s ) parents assumed configuration 7 (X1=3, X2=1) in 2 instances. Now breaking these Mij cases into sijk’s for node 3, we have:
s311 = 0 s312 = 0 s313 = 0 s321 = 1 s322 = 0 s323 = 0 s331 = 0 s332 = 1 s333 = 1 s341 = 0 s342 = 0 s343 = 1 s351 = 1 s352 = 0 s353 = 0 s361 = 1 s362 = 0 s363 = 0 s371 = 1 s372 = 1 s373 = 0 s381 = 0 s382 = 0 s383 = 1 s391 = 0 s392 = 1 s393 = 0
th That is, for example, 7 row in this table means when X3’s parents assumed configuration 7, X3 assumed the value “1” and “2” once (s371 = 1, s372 = 1), and the value “3” zero times (s373 = 0). We believe the introduction produced here is sufficient to follow the equation in Section 2.4. For further details, we refer the reader to “Neapolitan R.E. (2004) Learning Bayesian Networks. Prentice Hall”.
5 PART II: DAGs OF SIMULATED BNs
We first calculated following parameters for pathways listed in the KEGG database:
Average Std. Dev. # of Nodes 24.292 21.466 # of Edges 25.307 34.148 Max Degree 5.714 6.189 Average Degree 2.058 2.211 Density 0.180 0.264
We then created 8 synthetic BNs (in addition to widely used Asia and Alarm BNs) following parametric distribution found in KEGG. Synthetic BNs have (avg. ± st. dev.) 25.38 ± 13.87 nodes, 24.38 ± 13.87 links, and 1.93 ± 0.08 average degree reflecting a spectrum of typical biological networks.
DAG configuration of simulated BNs
Name Number of nodes Number of edges ALARMNET 37 47 ASIANET 8 8 BN1 19 18 BN2 8 7 BN3 21 20 BN4 36 35 BN5 18 17 BN6 29 28 BN7 19 18 BN8 53 52
6 6 3 8 7 1 5
2 1 1 1 1 4 1 0 2 9 2 3 2 4 1 6 2 5 4 3 4 6 4 3 3 2 8 2 6 2 1 1 3 6 2 3 2 1 8 3 1 2 7 1 3 3 0 9 1 7 3 5 5 1 2 1 7 1 6 7 1 4 3 7 1 8 1 9 5 9 1 0 1 1 1 5 3 1 9 2 0 8 1 2
2 2 1 3
ALARM network BN1
5 7
8 1 7
6 6 4 3 1 2 4 5 8 3 2
ASIA network BN2
7 1 4 9 1 3 1 5 1 6 6 1 7 6 7 2 0 1 5 1 0 2 1
4 1 4 5 1 7 9
2 1 2 3 5 1 2 1 1 1 7 8 1 8 1 0 1 3 1 1 8 1 2 3 4
1 8
1 9 1 6
BN3 BN5
1 2 0 2 5 3 6 2 3 2 6 3 0 1 8 1 2 2 2 2 8 2 5 1 4 9 1 3 1 8 2 3 1 0 2 4 3 3 2 9 2 8 6 6 3 7 1 1 5 1 3 2 1 2 7 1 9 2 9 1 6 5 1 5 3 5 1 6 9 2 4 1 9 1 1 2 2 1 1 7 5 1 7 2 7 8 3 4 1 1 4 3 2 3 1 1 4 7 1 2 1 0 2 0 2 2 3 8 4 2 6 2
BN4 BN6
8 1 8
5 1 3 9 1 6
2 1 7
8 1 4 6 1 0
4 7 1 5 1 1 1 2 1 9
1
3
BN7
33
25 50
21 18
28 11 34 15 19 1 16 24 43 20 7 17 2 30 39 40 49 9 37 8 10 47 26 35 48 6 3 29 44 4 13 31 27 46 45 32 14 51 23 12 42 5 53 36 41 22 52 38
BN8
9 PART III: CPTs of Simulated BNs
Conditional Probability Distribution of a node (i.e. a random variable in a Bayesian network model) can be represented in the form of a table, called the Conditional Probability Table (CPT). A CPT defines P(X(i) | X(Pa(i))), where X(i) is the ith node, and X(Pa(i)) are the parents of node i. Multidimensional arrays are used to store and list CPTs utilizing Bayes Net Toolbox (BNT) for Matlab (http://www.cs.ubc.ca/~murphyk/Software/BNT/bnt.html). If node i takes on I values and has k parents each of which take on Ik values, then the dimension of the array used to store the CPT for node i is I1 x I2 x…x Ik x I. In our representation below, and in the arrays holding CPTs, both nodes and nodes’ parents are shown in ascending order with respect to their node numbers. In our representation, values preceding “:” in the multidimensional array show possible values a node’s parent can take and values following “:” represent conditional probabilities for the values the node can take, all in ascending order. For example, assume we have a binary node “Node 1” with two binary parents “Node 3” and “Node 7”. Then, the CPT would have a form of 2x2x2 array and we would represent it as shown in the table below: Node 1 1 1 : 0.0377 0.9623 2 1 : 0.7766 0.2234 1 2 : 0.5753 0.4247 2 2 : 0.8009 0.1991
The probability P(Node1 = 1 | Node3 = 1, Node7 = 2) would be 0.5753, and would be indexed in the multidimensional array holding the CPTs as CPT(1,2,1) = 0.5753. Below is the set of CPTs for each BN used in MATLAB simulations. CPTs are listed in the order of nodes in each BN.
Ideal CPTs (used to generate “data following CPTs”) are chosen from a Dirichlet distribution and data that follow this CPT is generated using BNT. As for non-ideal CPTs (used to generate “data inconsistent with CPTs”), we have chosen initial Dirichlet hyper-parameters (prior beliefs) to be equal for each node, i.e. we have chosen null model to generate random data for each node, and generated data using BNT with this CPT. Therefore, underlying CPT calculated from this randomly generated data is considered to be nonideal CPT since the CPT is not generated according to the structure of given BN.
10 3 : 0.0100 0.0100 0.0100 0.9700 2 3 4 : 0.3000 0.6800 0.0100 0.0100 2 2 : 0.9800 0.0100 0.0100 2 1 2 2 : 0.0100 0.9900 IDEAL CPTs 1 3 : 0.9500 0.0400 0.0100 1 2 2 2 : 0.9500 0.0500 1 1 : 0.9800 0.0100 0.0100 1 : 0.3000 0.4000 0.3000 1 1 1 : 0.9700 0.0100 0.0100 0.0100 2 3 : 0.0100 0.9500 0.0400 2 2 2 2 : 0.0100 0.9900 2 1 : 0.9800 0.0100 0.0100 CPT of ALARM network 2 : 0.9800 0.0100 0.0100 2 1 1 : 0.9700 0.0100 0.0100 0.0100 1 4 : 0.9500 0.0400 0.0100 1 3 2 2 : 0.9500 0.0500 1 2 : 0.0100 0.9800 0.0100 1 : 0.9600 1 2 1 : 0.9700 0.0100 0.0100 0.0100 2 4 : 0.0100 0.0100 0.9800 2 3 2 2 : 0.0500 0.9500 2 2 : 0.4000 0.5900 0.0100 2 : 0.0400 1 : 0.9900 0.0100 2 2 1 : 0.9700 0.0100 0.0100 0.0100 1 1 3 2 : 0.1000 0.9000 1 3 : 0.0100 0.0100 0.9800 2 : 0.1000 0.9000 1 3 1 : 0.9700 0.0100 0.0100 0.0100 1 : 0.0100 0.0100 0.9800 2 1 3 2 : 0.0100 0.9900 2 3 : 0.3000 0.4000 0.3000 1 : 0.9200 2 3 1 : 0.9700 0.0100 0.0100 0.0100 2 : 0.0100 0.0100 0.9800 1 2 3 2 : 0.3000 0.7000 2 : 0.0300 1 : 0.0500 0.9000 0.0500 1 1 2 : 0.0100 0.9700 0.0100 0.0100 3 : 0.0400 0.9200 0.0400 2 2 3 2 : 0.0100 0.9900 1 1 : 0.9800 0.0100 0.0100 3 : 0.0500 2 : 0.0100 0.1900 0.8000 2 1 2 : 0.0100 0.4900 0.3000 0.2000 4 : 0.9000 0.0900 0.0100 1 3 3 2 : 0.3000 0.7000 2 1 : 0.9800 0.0100 0.0100 1 2 2 : 0.4000 0.5800 0.0100 0.0100 2 3 3 2 : 0.0100 0.9900 3 1 : 0.3000 0.6000 0.1000 1 : 0.8000 1 1 : 0.0500 0.9000 0.0500 2 2 2 : 0.1000 0.8400 0.0500 0.0100 1 1 : 0.9700 0.0100 0.0100 0.0100 1 1 1 3 : 0.9500 0.0500 1 2 : 0.9800 0.0100 0.0100 2 : 0.2000 2 1 : 0.9800 0.0100 0.0100 1 3 2 : 0.0100 0.9000 0.0800 0.0100 2 1 : 0.0100 0.9700 0.0100 0.0100 2 1 1 3 : 0.0100 0.9900 2 2 : 0.1000 0.8500 0.0500 1 2 : 0.0100 0.0900 0.9000 2 3 2 : 0.0100 0.2900 0.3000 0.4000 3 1 : 0.0100 0.9700 0.0100 0.0100 1 2 1 3 : 0.9900 0.0100 3 2 : 0.0500 0.4000 0.5500 1 : 0.9500 2 2 : 0.9500 0.0400 0.0100 1 1 3 : 0.0100 0.0100 0.9700 0.0100 4 1 : 0.0100 0.9700 0.0100 0.0100 2 2 1 3 : 0.0500 0.9500 1 3 : 0.9000 0.0900 0.0100 2 : 0.0500 2 1 3 : 0.0100 0.0100 0.0800 0.9000 1 2 : 0.9700 0.0100 0.0100 0.0100 1 3 1 3 : 0.9500 0.0500 2 3 : 0.0500 0.2000 0.7500 1 : 0.9500 0.0400 0.0100 1 2 3 : 0.2000 0.7500 0.0400 0.0100 2 2 : 0.0100 0.0100 0.9700 0.0100 2 3 1 3 : 0.0500 0.9500 3 3 : 0.0100 0.0900 0.9000 1 : 0.8000 2 : 0.0400 0.9500 0.0100 2 2 3 : 0.0500 0.2500 0.2500 0.4500 3 2 : 0.0100 0.0100 0.9700 0.0100 1 1 2 3 : 0.9500 0.0500 2 : 0.2000 3 : 0.0100 0.2900 0.7000 1 3 3 : 0.0100 0.0100 0.3800 0.6000 4 2 : 0.0100 0.0100 0.9700 0.0100 2 1 2 3 : 0.0100 0.9900 CPT of ASIA network 2 3 3 : 0.0100 0.0100 0.0800 0.9000 1 3 : 0.9700 0.0100 0.0100 0.0100 1 2 2 3 : 0.9900 0.0100 1 : 0.0100 1 : 0.0100 1 1 : 0.9700 0.0100 0.0100 0.0100 1 1 4 : 0.0100 0.0100 0.0100 0.9700 2 3 : 0.0100 0.0100 0.0100 0.9700 2 2 2 3 : 0.0500 0.9500 2 : 0.9900 2 : 0.9800 2 1 : 0.9700 0.0100 0.0100 0.0100 2 1 4 : 0.0100 0.0100 0.0100 0.9700 3 3 : 0.0100 0.0100 0.0100 0.9700 1 3 2 3 : 0.9900 0.0100 3 : 0.0100 1 2 : 0.0100 0.9700 0.0100 0.0100 1 2 4 : 0.2000 0.7000 0.0900 0.0100 4 3 : 0.0100 0.0100 0.0100 0.4300 2 3 2 3 : 0.0500 0.9500 1 : 0.5000 2 2 : 0.9700 0.0100 0.0100 0.0100 2 2 4 : 0.0100 0.1500 0.2500 0.5900 1 1 3 3 : 0.3000 0.7000 2 : 0.5000 1 : 0.0100 1 3 : 0.0100 0.0100 0.9700 0.0100 1 3 4 : 0.0100 0.0100 0.0100 0.9700 1 1 : 0.9800 0.0100 0.0100 2 1 3 3 : 0.0100 0.9900 2 : 0.9900 2 3 : 0.9700 0.0100 0.0100 0.0100 2 3 4 : 0.0100 0.0100 0.0100 0.9700 2 1 : 0.9800 0.0100 0.0100 1 2 3 3 : 0.9900 0.0100 1 : 0.0500 0.9500 1 4 : 0.0100 0.0100 0.0100 0.9700 1 2 : 0.0100 0.9800 0.0100 2 2 3 3 : 0.0100 0.9900 2 : 0.0100 0.9900 1 : 0.9500 2 4 : 0.9700 0.0100 0.0100 0.0100 1 1 : 0.9700 0.0100 0.0100 0.0100 2 2 : 0.9800 0.0100 0.0100 1 3 3 3 : 0.3000 0.7000 2 : 0.0500 2 1 : 0.9700 0.0100 0.0100 0.0100 1 3 : 0.0100 0.0100 0.9800 2 3 3 3 : 0.0100 0.9900 1 : 0.1000 0.9000 1 : 0.9500 0.0400 0.0100 3 1 : 0.9700 0.0100 0.0100 0.0100 2 3 : 0.6900 0.3000 0.0100 2 : 0.0100 0.9900 1 : 0.9500 2 : 0.0400 0.9500 0.0100 1 2 : 0.0100 0.9700 0.0100 0.0100 1 : 0.1000 0.8900 0.0100 2 : 0.0500 3 : 0.0100 0.0400 0.9500 2 2 : 0.6000 0.3800 0.0100 0.0100 1 1 1 1 : 0.0500 0.9500 2 : 0.0100 0.0900 0.9000 1 : 0.6000 0.4000 3 2 : 0.0100 0.9700 0.0100 0.0100 2 1 1 1 : 0.0100 0.9900 2 : 0.3000 0.7000 1 : 0.9000 1 1 1 : 0.9700 0.0100 0.0100 0.0100 1 3 : 0.0100 0.0100 0.9700 0.0100 1 2 1 1 : 0.0500 0.9500 1 1 : 0.9800 0.0100 0.0100 2 : 0.1000 2 1 1 : 0.9700 0.0100 0.0100 0.0100 2 3 : 0.5000 0.4800 0.0100 0.0100 2 2 1 1 : 0.0100 0.9900 2 1 : 0.3333 0.3333 0.3333 1 1 : 1.0000 0.0000 1 2 1 : 0.9700 0.0100 0.0100 0.0100 3 3 : 0.0100 0.0100 0.9700 0.0100 1 3 1 1 : 0.0500 0.9500 1 2 : 0.0100 0.9800 0.0100 2 1 : 1.0000 0.0000 1 : 0.9900 2 2 1 : 0.9700 0.0100 0.0100 0.0100 1 4 : 0.0100 0.0100 0.0100 0.9700 2 3 1 1 : 0.0100 0.9900 2 2 : 0.3333 0.3333 0.3333 1 2 : 1.0000 0.0000 2 : 0.0100 1 3 1 : 0.9700 0.0100 0.0100 0.0100 2 4 : 0.5000 0.4800 0.0100 0.0100 1 1 2 1 : 0.0500 0.9500 1 3 : 0.0100 0.0100 0.9800 2 2 : 0.0000 1.0000 2 3 1 : 0.9700 0.0100 0.0100 0.0100 3 4 : 0.0100 0.0100 0.0100 0.9700 2 1 2 1 : 0.0100 0.9900 2 3 : 0.3333 0.3333 0.3333 1 : 0.9900 1 1 2 : 0.0100 0.9700 0.0100 0.0100 1 2 2 1 : 0.0500 0.9500 1 : 0.9800 0.0200 2 : 0.0100 2 1 2 : 0.9500 0.0300 0.0100 0.0100 1 1 : 0.9700 0.0100 0.0100 0.0100 2 2 2 1 : 0.0100 0.9900 1 1 : 0.9800 0.0100 0.0100 2 : 0.0500 0.9500 1 2 2 : 0.9700 0.0100 0.0100 0.0100 2 1 : 0.9700 0.0100 0.0100 0.0100 1 3 2 1 : 0.0500 0.9500 2 1 : 0.3333 0.3333 0.3333 1 1 : 0.9500 0.0500 2 2 2 : 0.9700 0.0100 0.0100 0.0100 3 1 : 0.9700 0.0100 0.0100 0.0100 2 3 2 1 : 0.0100 0.9900 1 2 : 0.0100 0.9800 0.0100 1 1 : 0.9000 0.1000 2 1 : 0.9500 0.0500 1 3 2 : 0.0100 0.9700 0.0100 0.0100 1 2 : 0.0100 0.9700 0.0100 0.0100 1 1 3 1 : 0.0100 0.9900 2 2 : 0.3333 0.3333 0.3333 2 1 : 0.7000 0.3000 3 1 : 0.0500 0.9500 2 3 2 : 0.9500 0.0300 0.0100 0.0100 2 2 : 0.0100 0.9700 0.0100 0.0100 2 1 3 1 : 0.0100 0.9900 1 3 : 0.0100 0.0100 0.9800 1 2 : 0.8000 0.2000 1 2 : 0.1000 0.9000 1 1 3 : 0.0100 0.0100 0.9700 0.0100 3 2 : 0.0300 0.9500 0.0100 0.0100 1 2 3 1 : 0.0100 0.9900 2 3 : 0.3333 0.3333 0.3333 2 2 : 0.1000 0.9000 2 2 : 0.1000 0.9000 2 1 3 : 0.4000 0.5800 0.0100 0.0100 1 3 : 0.0100 0.0100 0.9700 0.0100 2 2 3 1 : 0.0100 0.9900 3 2 : 0.0100 0.9900 1 2 3 : 0.9700 0.0100 0.0100 0.0100 2 3 : 0.0100 0.0100 0.9700 0.0100 1 3 3 1 : 0.0100 0.9900 1 1 : 0.9800 0.0100 0.0100 2 2 3 : 0.9700 0.0100 0.0100 0.0100 3 3 : 0.0100 0.9400 0.0400 0.0100 2 3 3 1 : 0.0100 0.9900 2 1 : 0.9500 0.0400 0.0100 CPT of BN1 1 1 : 0.0500 0.9000 0.0500 1 3 3 : 0.0100 0.0100 0.9700 0.0100 1 4 : 0.9700 0.0100 0.0100 0.9700 1 1 1 2 : 0.1000 0.9000 3 1 : 0.3000 0.6900 0.0100 1 : 0.0580 2 1 : 0.9500 0.0400 0.0100 2 3 3 : 0.5000 0.4800 0.0100 0.0100 2 4 : 0.0100 0.0100 0.0100 0.9700 2 1 1 2 : 0.0100 0.9900 1 2 : 0.9500 0.0400 0.0100 2 : 0.9420 1 2 : 0.5000 0.4900 0.0100 1 1 4 : 0.0100 0.0100 0.0100 0.9700 3 4 : 0.0100 0.8800 0.1000 0.0100 1 2 1 2 : 0.9500 0.0500 2 2 : 0.0400 0.9500 0.0100 2 2 : 0.9800 0.0100 0.0100 2 1 4 : 0.3000 0.6800 0.0100 0.0100 2 2 1 2 : 0.0100 0.9900 3 2 : 0.0100 0.3000 0.6900 1 1 : 0.6387 0.3613 1 2 4 : 0.9700 0.0100 0.0100 0.0100 1 1 : 0.9800 0.0100 0.0100 1 3 1 2 : 0.9500 0.0500 1 3 : 0.8000 0.1900 0.0100 2 1 : 0.3358 0.6642 1 : 0.0100 0.9700 0.0100 0.0100 2 2 4 : 0.9700 0.0100 0.0100 0.0100 2 1 : 0.9800 0.0100 0.0100 2 3 1 2 : 0.0500 0.9500 2 3 : 0.0100 0.0400 0.9500 1 2 : 0.6118 0.3882 2 : 0.0100 0.0100 0.9700 0.0100 1 3 4 : 0.0100 0.0100 0.0100 0.9700 1 2 : 0.9800 0.0100 0.0100 1 1 2 2 : 0.1000 0.9000 3 3 : 0.0100 0.0100 0.9800 2 2 : 0.6977 0.3023
11 2 1 2 1 : 1.0000 0.0000 1 : 0.5123 0.4877 2 : 0.0390 1 1 : 0.8719 0.1281 2 : 0.6755 0.3245 1 : 1.0000 0.0000 1 2 2 1 : 0.4762 0.5238 2 : 0.5478 0.4522 2 1 : 0.7917 0.2083 2 : 0.0329 0.9671 2 2 2 1 : 0.5758 0.4242 1 : 0.6087 0.3913 1 2 : 0.0066 0.9934 1 : 0.5795 0.4205 1 1 1 2 : 0.6250 0.3750 1 : 0.2113 0.7887 2 : 0.6667 0.3333 2 2 : 0.6765 0.3235 2 : 0.5385 0.4615 1 : 0.2310 2 1 1 2 : 0.5333 0.4667 2 : 0.3929 0.6071 2 : 0.7690 1 2 1 2 : 0.2566 0.7434 1 1 1 : 0.8421 0.1579 1 : 0.5460 0.4540 1 1 : 0.3273 0.6727 2 2 1 2 : 0.6780 0.3220 1 : 0.4797 0.5203 2 1 1 : 0.0000 1.0000 2 : 0.8799 0.1201 2 1 : 0.3490 0.6510 1 1 : 0.8261 0.1739 1 1 2 2 : 0.4444 0.5556 2 : 0.4359 0.5641 1 2 1 : 0.6667 0.3333 1 2 : 0.6082 0.3918 2 1 : 0.5497 0.4503 2 1 2 2 : 0.5000 0.5000 2 2 1 : 0.8235 0.1765 1 1 1 : 0.9110 0.0890 2 2 : 0.5400 0.4600 1 2 : 0.8889 0.1111 1 2 2 2 : 0.5474 0.4526 1 : 0.9501 0.0499 1 1 2 : 0.0980 0.9020 2 1 1 : 0.7613 0.2387 2 2 : 0.0738 0.9262 2 2 2 2 : 0.6444 0.3556 2 : 0.6386 0.3614 2 1 2 : 0.6826 0.3174 1 2 1 : 0.6468 0.3532 1 : 1.0000 1 2 2 : 0.3000 0.7000 2 2 1 : 0.0000 1.0000 2 : 0.0000 1 : 0.6460 1 : 0.6667 0.3333 1 : 0.0000 1.0000 2 2 2 : 0.8661 0.1339 1 1 2 : 0.0000 0.0000 2 : 0.3540 2 : 0.3710 0.6290 2 : 0.1677 0.8323 2 1 2 : 0.0000 0.0000 1 : 0.2344 0.7656 1 : 0.9962 0.0038 1 2 2 : 0.0000 0.0000 2 : 0.4633 0.5367 1 : 0.4483 0.5517 1 : 0.2880 1 : 0.6073 0.3927 2 : 0.0021 0.9979 2 2 2 : 0.0000 0.0000 2 : 0.5053 0.4947 2 : 0.7120 2 : 0.9911 0.0089 1 : 0.4210 CPT of BN4 1 1 : 0.4611 0.5389 2 : 0.5790 1 : 0.0590 0.9410 CPT of BN2 1 : 0.4860 1 : 0.5062 0.4938 2 1 : 0.5810 0.4190 2 : 0.5969 0.4031 1 : 0.5720 2 : 0.5140 2 : 0.5772 0.4228 1 2 : 0.3552 0.6448 1 : 0.4607 0.5393 2 : 0.4280 2 2 : 0.6000 0.4000 2 : 0.4709 0.5291 1 : 0.7440 1 : 0.7505 0.2495 1 : 0.4820 2 : 0.2560 1 1 1 : 0.7325 0.2675 2 : 0.5372 0.4628 2 : 0.5180 1 1 1 : 0.8542 0.1458 1 : 1.0000 2 1 1 : 0.0000 1.0000 2 1 1 : 0.7182 0.2818 2 : 0.0000 1 : 0.0320 1 2 1 : 0.1111 0.8889 1 : 0.4640 0.5360 1 : 0.7370 0.2630 1 2 1 : 0.8230 0.1770 2 : 0.9680 2 2 1 : 0.0000 1.0000 2 : 0.4153 0.5847 2 : 0.4807 0.5193 2 2 1 : 0.1647 0.8353 1 1 : 0.3959 0.6041 1 1 2 : 0.0959 0.9041 1 1 2 : 0.1839 0.8161 2 1 : 0.3613 0.6387 1 1 1 : 0.8333 0.1667 2 1 2 : 1.0000 0.0000 1 : 0.3762 0.6238 1 : 0.5740 2 1 2 : 0.5639 0.4361 1 2 : 0.4225 0.5775 2 1 1 : 1.0000 0.0000 1 2 2 : 0.0205 0.9795 2 : 0.3121 0.6879 2 : 0.4260 1 2 2 : 0.6224 0.3776 2 2 : 0.3509 0.6491 1 2 1 : 0.8519 0.1481 2 2 2 : 1.0000 0.0000 2 2 2 : 0.3878 0.6122 2 2 1 : 0.3811 0.6189 1 1 : 0.0204 0.9796 1 : 0.5183 0.4817 1 1 : 0.4843 0.5157 1 1 2 : 0.6250 0.3750 1 : 0.9850 2 1 : 0.0124 0.9876 2 : 0.2929 0.7071 1 : 0.1806 0.8194 2 1 : 0.3385 0.6615 2 1 2 : 0.7813 0.2188 2 : 0.0150 1 2 : 0.9613 0.0387 2 : 0.1351 0.8649 1 2 : 0.6212 0.3788 1 2 2 : 0.1765 0.8235 2 2 : 0.0435 0.9565 1 1 : 0.9941 0.0059 2 2 : 0.8027 0.1973 2 2 2 : 0.0479 0.9521 1 : 0.7410 2 1 : 0.7232 0.2768 1 : 0.2158 0.7842 2 : 0.2590 1 : 0.5830 1 2 : 0.0000 0.0000 2 : 0.6718 0.3282 1 : 0.4790 0.5210 1 : 0.7470 2 : 0.4170 2 2 : 0.0000 0.0000 2 : 0.4850 0.5150 2 : 0.2530 1 : 0.9880 1 : 0.3220 0.6780 2 : 0.0120 1 1 : 0.0377 0.9623 1 : 0.9870 2 : 0.5351 0.4649 CPT of BN5 1 : 0.5400 0.4600 2 1 : 0.7766 0.2234 2 : 0.0130 1 1 : 0.6098 0.3902 2 : 0.4179 0.5821 1 : 0.4290 1 2 : 0.5753 0.4247 1 : 0.4460 2 1 : 0.8141 0.1859 2 : 0.5710 2 2 : 0.8009 0.1991 1 : 0.5511 0.4489 2 : 0.5540 1 2 : 0.3821 0.6179 1 : 0.5968 0.4032 2 : 0.5682 0.4318 2 2 : 0.4317 0.5683 2 : 0.7466 0.2534 1 1 1 : 0.4463 0.5537 1 : 0.3810 0.6190 1 : 0.1674 0.8326 2 1 1 : 0.5549 0.4451 2 : 0.4385 0.5615 1 : 0.3980 2 : 0.8333 0.1667 1 1 1 : 0.4659 0.5341 1 : 0.0500 1 2 1 : 0.0000 1.0000 2 : 0.6020 2 1 1 : 0.4683 0.5317 2 : 0.9500 2 2 1 : 1.0000 0.0000 1 : 0.7440 1 : 0.3710 1 2 1 : 0.6079 0.3921 1 1 2 : 0.6431 0.3569 2 : 0.2560 1 : 0.8720 2 : 0.6290 2 2 1 : 0.1912 0.8088 1 : 0.0433 0.9567 2 1 2 : 0.2803 0.7197 2 : 0.1280 1 1 2 : 0.5000 0.5000 2 : 0.0065 0.9935 1 2 2 : 0.0000 1.0000 1 : 0.2520 1 : 0.6809 0.3191 2 1 2 : 0.2727 0.7273 2 2 2 : 1.0000 0.0000 2 : 0.7480 1 : 0.6256 0.3744 2 : 0.3455 0.6545 1 2 2 : 0.3333 0.6667 1 1 1 1 : 0.2500 0.7500 2 : 0.6927 0.3073 2 2 2 : 0.3333 0.6667 2 1 1 1 : 0.4000 0.6000 1 : 0.8811 0.1189 1 : 0.5780 0.4220 1 : 0.5010 1 2 1 1 : 0.6765 0.3235 2 : 0.8388 0.1612 2 : 0.4688 0.5313 1 : 0.5157 0.4843 2 : 0.4990 1 : 0.4120 2 2 1 1 : 0.4684 0.5316 2 : 0.6174 0.3826 2 : 0.5880 1 1 2 1 : 0.5000 0.5000 CPT of BN3 1 : 0.9610 1 : 0.8205 0.1795
12 1 : 0.1220 1 : 0.7300 1 : 0.4850 1 1 : 0.3949 0.6051 2 : 0.2270 2 : 0.8780 1 : 0.2349 0.7651 2 : 0.2700 2 : 0.5150 2 1 : 0.4023 0.5977 2 : 0.1328 0.8672 1 2 : 0.4248 0.5752 1 : 0.4550 1 : 0.4502 0.5498 1 : 0.4317 0.5683 1 : 0.4330 2 2 : 0.4385 0.5615 2 : 0.5450 2 : 0.4367 0.5633 1 : 0.0115 0.9885 2 : 0.7573 0.2427 2 : 0.5670 2 : 0.0280 0.9720 1 : 0.0000 1 : 0.0990 1 : 0.3840 1 : 0.6042 0.3958 1 1 : 0.4604 0.5396 2 : 1.0000 2 : 0.9010 2 : 0.6160 1 : 0.3960 2 : 0.5704 0.4296 2 1 : 0.7413 0.2587 2 : 0.6040 1 2 : 0.6816 0.3184 1 : 0.3880 0.6120 1 : 0.1736 0.8264 1 : 0.0000 1 : 0.8317 0.1683 2 2 : 0.3142 0.6858 2 : 0.5341 0.4659 2 : 0.5347 0.4653 2 : 1.0000 1 : 0.4280 2 : 0.0964 0.9036 2 : 0.5720 1 1 1 : 0.0000 1.0000 1 : 0.3570 1 : 0.6923 0.3077 1 : 0.5738 0.4262 1 1 : 0.6185 0.3815 2 1 1 : 0.4444 0.5556 2 : 0.6430 2 : 0.3091 0.6909 2 : 0.4966 0.5034 1 : 0.7580 2 1 : 0.5084 0.4916 1 2 1 : 0.5714 0.4286 2 : 0.2420 1 2 : 0.6364 0.3636 2 2 1 : 0.8525 0.1475 1 1 : 0.5556 0.4444 1 : 0.4322 0.5678 1 : 0.7570 2 2 : 0.5489 0.4511 1 1 2 : 0.3125 0.6875 2 1 : 0.4136 0.5864 2 : 0.3853 0.6147 2 : 0.2430 1 1 : 0.5039 0.4961 2 1 2 : 0.7647 0.2353 1 2 : 0.6266 0.3734 2 1 : 0.5025 0.4975 1 : 0.3369 0.6631 1 2 2 : 0.1364 0.8636 2 2 : 0.5369 0.4631 1 1 1 : 0.6593 0.3407 1 1 : 0.4235 0.5765 1 2 : 0.5357 0.4643 2 : 0.2285 0.7715 2 2 2 : 0.1948 0.8052 2 1 1 : 0.4926 0.5074 2 1 : 0.4700 0.5300 2 2 : 0.3852 0.6148 1 : 0.2381 0.7619 1 2 1 : 0.4507 0.5493 1 2 : 0.3048 0.6952 1 : 0.3910 1 : 0.2990 0.7010 2 : 0.2737 0.7263 2 2 1 : 0.7342 0.2658 2 2 : 0.4565 0.5435 1 : 0.5934 0.4066 2 : 0.6090 2 : 0.1243 0.8757 1 1 2 : 0.2840 0.7160 2 : 0.1325 0.8675 1 : 0.6360 2 1 2 : 0.4200 0.5800 1 : 0.9740 1 : 0.1179 0.8821 1 : 0.0470 2 : 0.3640 1 2 2 : 0.4919 0.5081 2 : 0.0260 1 : 0.4000 0.6000 2 : 0.1447 0.8553 2 : 0.9530 2 2 2 : 0.4462 0.5538 2 : 0.6173 0.3827 1 : 0.4564 0.5436 1 : 0.6335 0.3665 1 : 0.1941 0.8059 1 : 0.0020 2 : 0.6102 0.3898 1 : 0.0573 0.9427 2 : 0.3401 0.6599 1 : 0.5918 0.4082 2 : 0.3406 0.6594 2 : 0.9980 2 : 0.8916 0.1084 2 : 0.6080 0.3920 1 : 0.1402 0.8598 1 : 0.2870 1 : 0.9591 0.0409 1 : 0.3400 2 : 0.9364 0.0636 1 1 : 0.0000 0.0000 2 : 0.7130 1 : 0.5574 0.4426 2 : 0.3058 0.6942 2 : 0.6600 2 1 : 0.4444 0.5556 2 : 0.2687 0.7313 1 : 0.9980 1 2 : 0.0000 0.0000 1 1 : 0.0000 0.0000 1 1 : 0.5076 0.4924 1 1 : 0.6118 0.3882 2 : 0.0020 2 2 : 0.6712 0.3288 2 1 : 0.4473 0.5527 1 : 0.1023 0.8977 2 1 : 0.2166 0.7834 2 1 : 0.5887 0.4113 1 2 : 0.0000 0.0000 2 : 0.2824 0.7176 1 2 : 0.5700 0.4300 1 2 : 0.2297 0.7703 1 : 0.5510 1 : 0.8773 0.1227 2 2 : 0.7869 0.2131 2 2 : 0.8110 0.1890 2 2 : 0.5333 0.4667 2 : 0.4490 2 : 0.6936 0.3064 1 1 : 0.1509 0.8491 1 : 0.7109 0.2891 2 1 : 0.5918 0.4082 CPT of BN7 1 : 0.4458 0.5542 1 : 0.9979 0.0021 1 : 0.5171 0.4829 2 : 0.4692 0.5308 1 2 : 0.8889 0.1111 1 : 0.5265 0.4735 2 : 0.3641 0.6359 2 : 0.0135 0.9865 2 : 0.4349 0.5651 2 2 : 0.8073 0.1927 2 : 0.6333 0.3667 1 : 0.3689 0.6311 1 : 0.4971 0.5029 1 : 0.6283 0.3717 1 : 0.7809 0.2191 2 : 1.0000 0.0000 1 : 0.4250 1 : 0.3810 2 : 0.5489 0.4511 2 : 0.6905 0.3095 2 : 0.5086 0.4914 2 : 0.5750 2 : 0.6190 1 1 : 0.4820 0.5180 1 : 0.0000 1 : 0.3698 0.6302 1 : 0.6283 0.3717 2 1 : 0.4925 0.5075 1 : 0.9850 0.0150 1 : 0.0000 1.0000 2 : 1.0000 2 : 0.5325 0.4675 2 : 0.5401 0.4599 1 2 : 0.5960 0.4040 2 : 1.0000 0.0000 2 : 1.0000 0.0000 2 2 : 0.4479 0.5521 1 : 0.0000 0.0000 1 : 0.8348 0.1652 1 : 0.3563 0.6437 1 : 0.5491 0.4509 1 1 1 : 1.0000 0.0000 2 : 0.4150 0.5850 2 : 0.5256 0.4744 2 : 0.7168 0.2832 1 : 0.1897 0.8103 2 : 0.3444 0.6556 2 1 1 : 0.0000 1.0000 2 : 0.7611 0.2389 1 2 1 : 0.6170 0.3830 1 : 0.7002 0.2998 1 : 0.6603 0.3397 1 1 : 0.4375 0.5625 1 : 0.4974 0.5026 2 2 1 : 0.5754 0.4246 2 : 0.3831 0.6169 2 : 0.4783 0.5217 2 1 : 0.4470 0.5530 CPT of BN6 2 : 0.4530 0.5470 1 1 2 : 0.0000 0.0000 1 2 : 0.4286 0.5714 1 1 : 0.7500 0.2500 2 1 2 : 0.0000 0.0000 1 : 0.6609 0.3391 1 : 0.3376 0.6624 2 2 : 0.5369 0.4631 2 1 : 0.4624 0.5376 1 : 0.0016 0.9984 1 2 2 : 0.9036 0.0964 2 : 0.7238 0.2762 2 : 0.6955 0.3045 1 2 : 0.8333 0.1667 2 : 0.5725 0.4275 2 2 2 : 0.2100 0.7900 1 : 0.7510 2 2 : 0.7121 0.2879 CPT of BN8 1 : 0.7730 2 : 0.2490
13 1 2 : 0.5040 0.4960 1 : 0.6080 0.3920 2 2 : 0.7150 0.2850 2 : 0.5551 0.4449 1 : 0.5062 0.4938 1 : 0.5340 2 : 0.1629 0.8371 2 : 0.4660 1 1 : 0.1978 0.8022 1 1 : 0.5588 0.4412 2 1 : 0.7406 0.2594 2 1 : 0.4977 0.5023 1 2 : 0.3750 0.6250 1 2 : 0.3951 0.6049 2 2 : 0.0526 0.9474 2 2 : 0.3890 0.6110 1 : 0.4966 0.5034 1 1 : 0.9882 0.0118 2 : 0.3102 0.6898 2 1 : 0.0000 0.0000 1 2 : 1.0000 0.0000 1 : 0.7480 2 2 : 1.0000 0.0000 2 : 0.2520
1 : 0.4383 0.5617 1 : 0.3490 2 : 0.4393 0.5607 2 : 0.6510
1 1 1 : 0.8304 0.1696 1 : 0.6340 0.3660 2 1 1 : 0.2561 0.7439 2 : 0.5528 0.4472 1 2 1 : 0.5652 0.4348 2 2 1 : 0.4800 0.5200 1 1 2 : 0.5932 0.4068 2 1 2 : 0.6306 0.3694 1 2 2 : 0.6563 0.3438 2 2 2 : 0.4262 0.5738
1 1 : 0.8214 0.1786 2 1 : 0.8076 0.1924 1 2 : 0.2791 0.7209 2 2 : 0.5507 0.4493
1 : 0.3530 2 : 0.6470
1 : 0.0390 2 : 0.9610
1 : 0.3770 2 : 0.6230
1 : 0.9951 0.0049 2 : 0.6057 0.3943
1 1 : 0.5714 0.4286 2 1 : 0.5228 0.4772 1 2 : 0.9400 0.0600 2 2 : 0.3679 0.6321
1 : 0.4147 0.5853 2 : 0.4775 0.5225
1 1 : 0.4924 0.5076 2 1 : 0.4333 0.5667
14