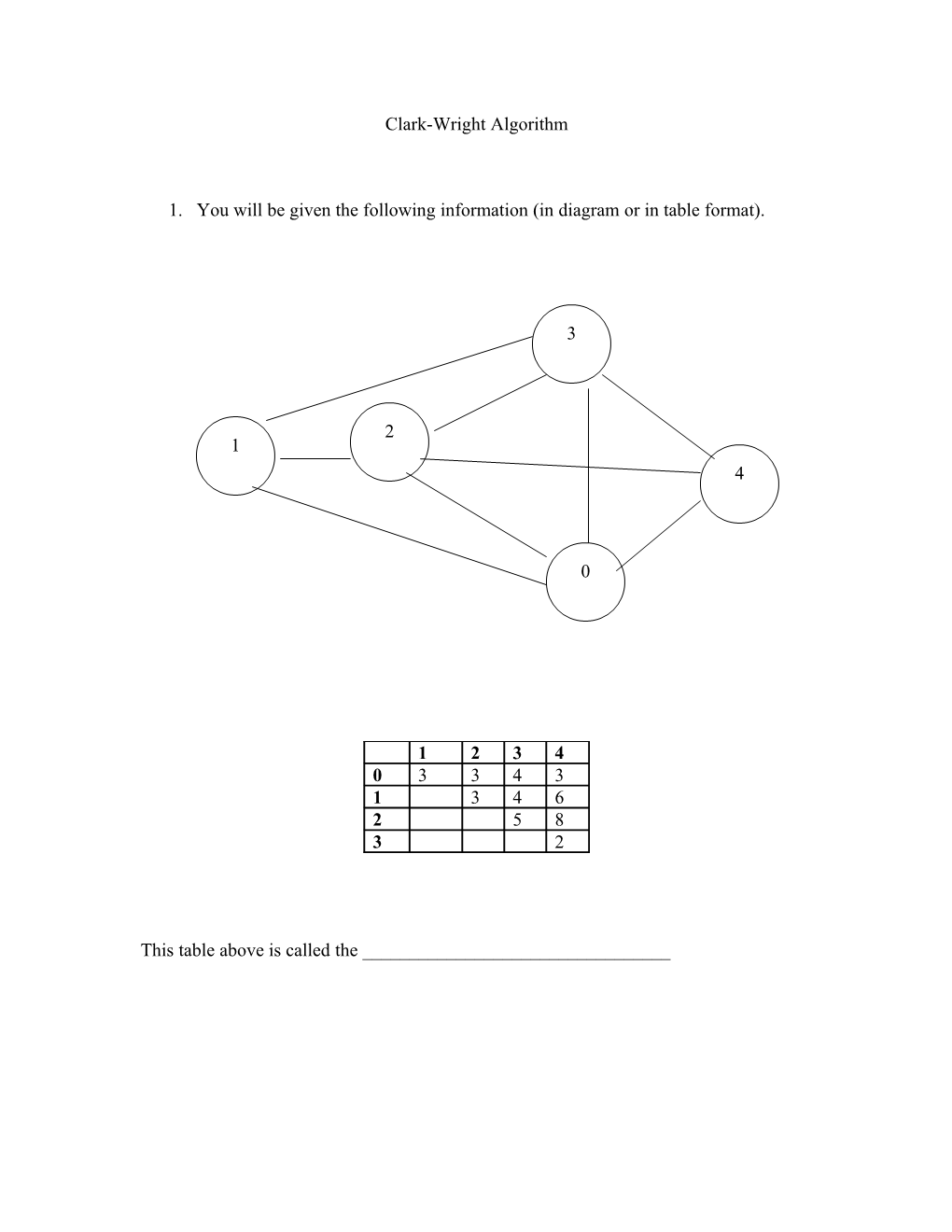
Clark-Wright Algorithm

1. You will be given the following information (in diagram or in table format).

1 2 3 4 0 3 3 4 3 1 3 4 6 2 5 8 3 2

This table above is called the ______2. Develop the Net Savings Matrix

1 2 3 4 0 ….. ….. ….. ….. 1 3 2 3

Net Savings of going 0 to 1 to 2 to 0 (rather than 0 to 1 and 0 to 2 and back to 0) is:

= D0i + D0j – Dij

= 3 + 3 – 3

Distance between 0 and 1 = D0i = D01 = 3 Distance between 0 and 2 = D0j = D02 = 3 Distance between 1 and 2 = Dij = D12 = 3

1 2 3 4 0 ….. ….. ….. ….. 1 3 3 0 2 2 0 3 5

Net Savings per Route

1 to 3 3 + 4 – 4 = 3 1 to 4 3 + 3 – 6 = 0 2 to 3 3 + 4 – 5 = 2 2 to 4 3 + 3 – 8 = -2 or 0 3 to 4 4 + 3 -2 = 5

This table above is called the ______3. Run the Optimization

A) Start with the most inefficient route 3 + 3 + 3 + 3 + 4 + 4 + 3 + 3 = 26 miles

4 2 3 1 4

a. Original Net Savings Matrix with the bold values being the original “T” values.

1 2 3 4 0 2 2 2 2 1 3 3 0 2 2 0 3 5

b. Find the highest number on the Net Savings Matrix and see if the route satisfies our assumptions.

 Route 3 to 4 has a savings of 5 miles if we don’t go back to the warehouse.  Does it meet the assumptions?

st . 1 Assumption is that the D0i and D0j do not have a “T” value of 0 Answer: This is true. In this model, D03 currently has T = 2 and D04 has T = 2

nd . 2 Assumption is that D0i and D0j are not on the same path Answer: This is true.

 Reroute the original trip from: 0 – 3 – 0 – 4 - 0 to: 0 – 3 – 4 – 0

c. Update the Net Savings table with the new T value

1 2 3 4 0 2 2 2 2 1 3 3 0 2 2 0 3 1 B) Go to the next highest value on the Net Savings Matrix. It is 3 (doesn’t matter which 3 you choose)

1 2 3 4 0 2 2 2 2 1 3 3 0 2 2 0 3 1

 Does it meet the assumptions?

nd . 2 Assumption is that D01 and D02 are not on the same path Answer: This is true.

 Reroute the original trip from: 0 – 1 – 0 – 2 - 0 to: 0 – 1 – 2 – 0

0 a. Update the Net Savings table with the new T value

1 2 3 4 0 2 2 2 2 1 1 3 0 2 2 0 3 1

C) Go to the next highest value on the Net Savings Matrix. It is 3 (trips between 1 and 3).

1 2 3 4 0 2 2 2 2 1 1 3 0 2 2 0 3 1

 Does it meet the assumptions?

nd . 2 Assumption is that D01 and D02 are not on the same path Answer: This is true.

 Reroute the original trip from: 0 – 1 – 0 – 3 - 0 to: 0 – 1 – 3 – 0 3

a. Update the Net Savings table with the new T value

1 2 3 4 0 2 2 2 2 1 1 1 0 2 2 0 3 1

Now, take a look at the model. We can eliminate the trip between 0 and 3 because it serves no purpose. The most efficient route becomes 0 – 2 – 1 – 3 – 4 – 0 or 3 + 3 + 4 + 2 + 3 = 15 miles 3