Handout 11 (Chapter 12): Simple Linear Regression and Correlation

STAT 211

 Is there a relationship between two numeric random variables?  Can we describe this relationship with a model?  Can we use this model to predict the future values?

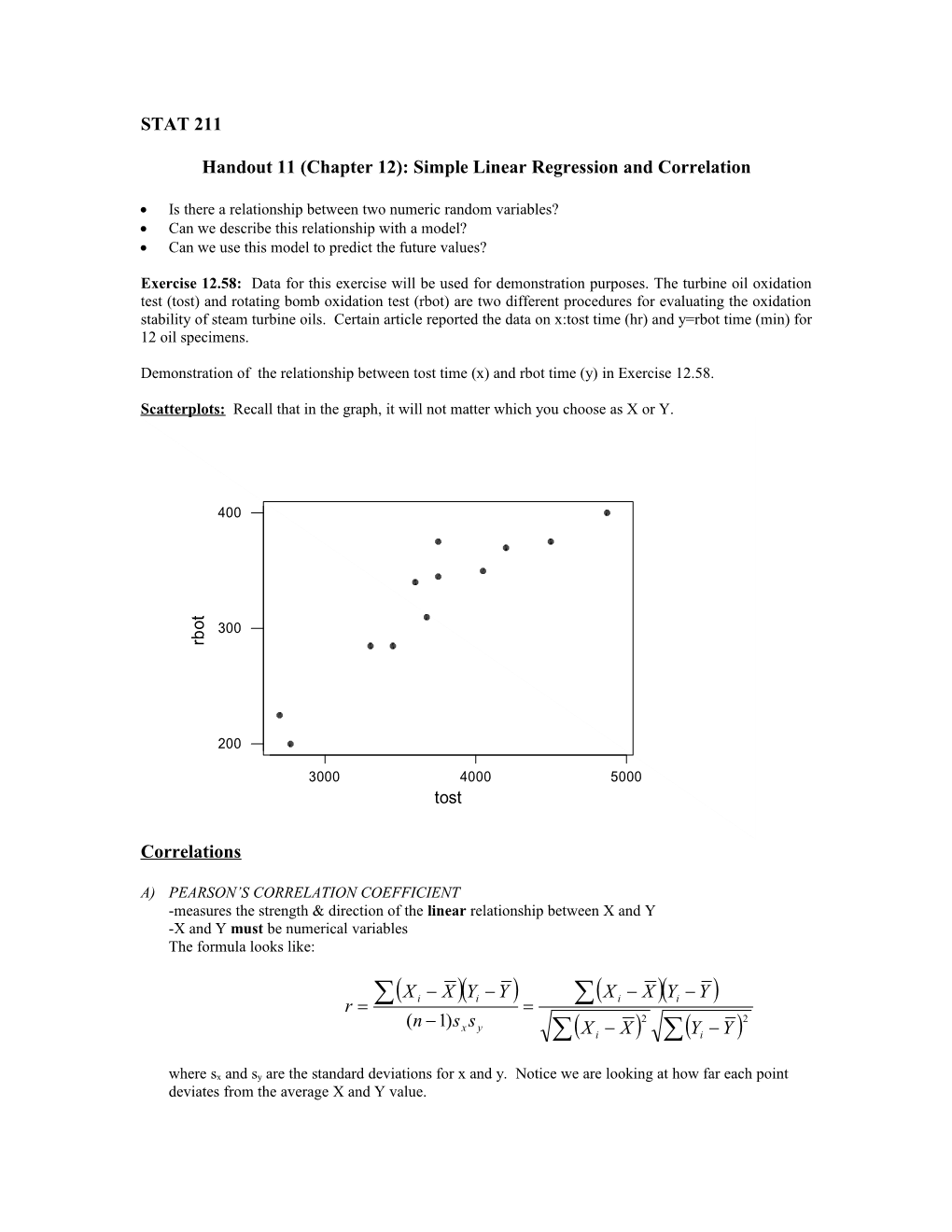
Exercise 12.58: Data for this exercise will be used for demonstration purposes. The turbine oil oxidation test (tost) and rotating bomb oxidation test (rbot) are two different procedures for evaluating the oxidation stability of steam turbine oils. Certain article reported the data on x:tost time (hr) and y=rbot time (min) for 12 oil specimens.

Demonstration of the relationship between tost time (x) and rbot time (y) in Exercise 12.58.

Scatterplots: Recall that in the graph, it will not matter which you choose as X or Y.

o 300 b r

3000 4000 5000 tost

Correlations

A) PEARSON’S CORRELATION COEFFICIENT -measures the strength & direction of the linear relationship between X and Y -X and Y must be numerical variables The formula looks like:

X  X Y  Y  X  X Y  Y  r   i i   i i 2 2 (n 1)s x s y X i  X  Yi  Y 

where sx and sy are the standard deviations for x and y. Notice we are looking at how far each point deviates from the average X and Y value. Properties of Pearson’s Correlation Coefficient  r<0 implies a negative relationship, r>0 implies a positive relationship, r=0 no apparent relationship.  -1 r 1  r=1 or –1 happens only when the points lie on an exact line  r0.8 implies a strong relationship, 0.5<r<0.8 a moderate relationship, & r0.5 implies a weak one

Note: It is pretty hard to tell the difference in graphs with correlation under 0.5! However, the larger the sample size, the easier it is to see the correlation!

CAUTION: Scatterplots with weak correlations are just scattered points. You could have a curved shape (i.e.- a parabola) that fits the data perfectly, but it will have a very weak Pearson’s correlation coefficient.

 The correlation is the same no matter which variable is designated X or Y  The value of r does not depend upon the units of measurement. For example, the correlation between height in inches and shoe size will be the same as the correlation between height in feet and shoe size.

Using the MINITAB program the following is computed for the exercise.

Pearson correlation of tost and rbot = 0.923 P-Value = 0.000

Note the correlation for x (tost time) and y (rbot time) is 0.923. The 0.000 is the P-value for testing

H 0 :  XY  0 (the true correlation is zero. It means there is no relation between x and y) versus

H a :  XY  0 (the true correlation is not zero. It means there is a relation between x and y).

r n  2 The formal test has the test statistics t  =7.5852 with n-2 degrees of freedom. 1 r 2 Since this was a two tailed test, P-value=2P(t>7.5852)

The correlation for x vs. x and y vs. y is 1. Why?

IMPORTANT !!!! Just because two variables are highly correlated does NOT mean that one causes the other!!!!

B) SPEARMAN'S RANK CORRELATION (rs) Recall, Pearson’s r is calculated with means and thus would be affected by outliers. Thus Spearman’s method provides us with an alternative that is robust to outliers. Spearman’s can identify both linear and nonlinear relationships. The actual observed data is not used – the ranks are. That is, they replace the smallest X with a 1, the next with a 2, and so on. The same is done for Y. For example:

for (12.3, 2.7) (10.4, 3.2) (13.2,3.0) you would use (2,1) (1,3) (3,2)

Then the Pearson formula is just applied to these ranks. Thus, rs is interpreted just like r: has values between –1 and 1, with 1 indicating a strong relationship and 0 a weak.

Spearman’s correlation of tost and rbot = 0.944 P-Value = 0.000

The correlation is 0.944 – close to Pearson's r.

Purposes for fitting equations to data sets:  To summarize and condense a data set in order to obtain predictive formulas  To reject or confirm a proposed mathematical relation  To assist in the search for a mathematical relation  To perform a quantitative comparison of two or more data sets

Where do we find our equation for the least squares line?

Regression analysis is a general approach for obtaining a prediction function using a sample data. We work with a dependent variable (Y, response or endogenous variable), independent variable (X's, predictor or ^ exogenous variable) and the predicted value for a given level of X, Y . The method of least squares finds particular line where the aggregate deviation of the data points above or below it is minimized.

Least Squares Regression Line-slope & intercept Now if we have an idea that there is some sort of relationship, we are interested in some way to summarize that relationship. We want to find a line that “best fits” the points – least squares regression line - so that we can predict values for Y if we know X. The “best fit” line is the line that in some sense is closest to all of the data points simultaneously.

The vertical distances from each point to the line is drawn. These are the residuals, denoted by e. If the point is above the line, this distance is +, below it is -. If we added up all of the e’s, we would get zero (we will check this in lecture) If we add up all of the squares of the residuals, we get a measure of how far away from the data our line is. The “best line” will be the one with the minimum sum of the squares – thus it is called the “Least Squares Regression Line”.

Simple Linear Regression: Y   0  1 x  e , where n observations included, the parameters  0 and

1 are constants whose "true" values are unknown and must be estimated from the data.  The variables Y and x are theoretically related to one another by the equation of the straight line,  The data set is typical of the behavior of the process under study.

 The Yi, i=1,2,….,n, are pairwise statistically independent of one another. 2  The Yi are random variables possessing the same variance,  .  For each data point, there are no outliers that have arisen under unusual, accidental, or careless circumstances.  The uncontrolled random error, e associated with the Y is normally independently distributed with mean 0 and the constant variance,  2 .

Obtaining the best estimates for  0 (intercept) and 1 (slope): ^  The estimate of  i (residual), ei  yi  y i  yi  (b0  b1 xi ) n n 2 2  Minimize ei  (yi  b0  b1 xi ) (i.e., take a first derivative with respect to b0 and b1 ) i1 i1  Resulting equations are called normal equations n n  yi  n b0  b1   xi i1 i1 n n n 2  xi  yi  b0   xi  b1   xi i1 i1 i1

 Estimated linear regression coefficients are n  _  _  n _ _  xi  x yi  y  xi yi  n x y i1    i1 b1   n _ 2 n _ 2   x 2  n x  xi  x  i i1   i1 _ _

b0  y b1  x ^  The estimated linear regression equation, y  b0  b1  x

If you write y as the function of x (regress y on x), the following output can be obtained for exercise 12.58:

The regression equation is rbot = - 13.9 + 0.0902 tost

Predictor Coef SE Coef T P Constant -13.85 44.78 -0.31 0.763 tost 0.09024 0.01188 7.59 0.000

S = 25.15 R-Sq = 85.2% R-Sq(adj) = 83.7%

Analysis of Variance Source DF SS MS F P Regression 1 36489 36489 57.67 0.000 Residual Error 10 6328 633 Total 11 42817

Unusual Observations Obs tost rbot Fit SE Fit Residual St Resid 3 3750 375.00 324.56 7.27 50.44 2.09R

R denotes an observation with a large standardized residual

The slope and intercept for your equation is found under the coefficient column. Which is the slope and which is the intercept? What is the least squares regression line in this example?

Minitab gives you the following output for simple linear regression Predictor (y) Coef SE Coef T P _  2  1 (x)  b0 Constant b0 s  s  p-value b0  _  s n 2 b0  (xi  x)  _ b 2 1 tost (x) b1 s  s / (x  x) p-value b1  i s i1 b1 Analysis of Variance Source DF SS MS F P Regression 1 SSR MSR MSR/MSE p-value Residual Error n-2 SSE MSE Total n-1 SST

rbot  13.85  0.09024tost has two interpretations:

(i) It is a point estimate of the mean value of rbot when tost is given. (ii) It is a point prediction of an individual rbot to be observed when tost is given.

Estimate of average rbot when tost =3700 is -13.85+0.09024(3700)=320.038 Predicted rbot when tost=3700 is -13.85+0.09024(3700)= 320.0

Estimate of average rbot when tost =500 cannot be computed using the equation Predicted rbot when tost=500 cannot be computed using the equation

SSE = 6328 is the unexplained variation: measure of y's variation that can be attributed to an approximate linear relationship.

SST = 42817 explains the deviations of y from the sample mean of y

Coefficient of Determination, R2 : Measure what percent of Y's variation is explained by the X variables via the regression model. It tells us the proportion of SST that is explained by the fitted equation. Note that SSE is the proportion of SST that is not explained by the model. SSR SSE R 2   1 SST SST Only in simple linear regression, R 2  r 2 where r is the Pearson’s correlation coefficient.

2 2 n 1 SSE  (n 1)  R 1 Adjusted R  1     n  2 SST  n  2  Both will always be between 0 and 1 indicating strong linear relationship between X and Y if it is close to 1 and very weak relationship between X and Y if it is close to 0. It is 0 (No linear relationship) when SSE= SST.

85.2% of Y's variation is explained by the X variables via the regression the example above.

Notice that R2 =r2 = (0.923)2 only if you have one X and one Y variable in your regression model (Simple Linear Regression).

Eventhough estimated variance and the coefficient of determination are given in your ANOVA table, the following is the way how they are calculated: ^  2  s 2  SSE /(n  2)  6328 /10  633 : MSE ^   s  6328/10  25.16 : Root MSE SSE 6328 r 2  1  1  0.852 : Coefficient of determination SST 42817 Approximately 85.2% of the observed variation in rbot can be attributed to the probabilistic linear relationship with tost. ^ ^ The following residuals ( e  y  y ) and predicted response ( y ) computed by Minitab. If you compute them by hand, you will get slightly different number because of the rounding. My suggestion is for you to use these numbers as it is given on the output unless otherwise is asked.

Tost rbot residual predicted rbot 4200 370 4.8285 365.171 3600 340 28.9745 311.025 3750 375 50.4380 324.562 3675 310 -7.7937 317.794 4050 350 -1.6350 351.635 2770 200 -36.1235 236.124 4870 400 -25.6345 425.634 4500 375 -17.2444 392.244 3450 285 -12.4890 297.489 2700 225 -4.8065 229.807 3750 345 20.4380 324.562 3300 285 1.0475 283.952

Notice that some of the residuals are positive and some others are negative. All add up to zero.

The intercept and the slope are calculated for this data. Since the slope is a numeric number other than zero, we may think x and y are related. Is it true in the population?

H 0 : 1  0 (no relation between x and y)

H a : 1  0 (x and y are related)

b1  0 0.09024  0 Test statistics: t    7.59  t  t =2.2288. H is rejected and data s 0.01188  / 2;df 0.025;10 0 b1 supports the relation between x and y . Note that is the estimated slope, s is the standard error for b1 b1 b1 , 5% significance is used with the error degrees of freedom. The formal test would be the following:

H 0 : 1  10

H a : 1  10

b1  10 Test statistics: t  where 10 is the value slope is compared with. stdb1  Decision making can be done by using error degrees of freedom for any other t test we have discussed before (either using the P-value or the rejection region method)

b  t s The 100(1-)% confidence interval for 1 is 1  / 2;df b1

For our example, 95% confidence interval for 1 is 0.09024 2.2288(0.01188)=(0.0638 , 0.1167)

You can also test for H a : 1  10 or H a : 1  10 . Example 2: I am interested in seeing the benefits of attending the class and taking quizzes. I will regress your overall grade (y) after the 3rd exam on the number of quizzes taken (x). The following output is obtained using Excel.

Regression Statistics Multiple R 0.537728 R Square 0.289152 Adjusted R Square 0.285978 Standard Error 9.875656 Observations 226

ANOVA Significance df SS MS F F Regression 1 8886.462 8886.462 91.11648 2.46E-18 Residual 224 21846.4 97.52859 Total 225 30732.87

Coefficient Standard Upper s Error t Stat P-value Lower 95% 95% Intercept 60.93859 1.913907 31.83989 4.18E-85 57.16702 64.71015 X Variable 1 2.795969 0.29291 9.545495 2.46E-18 2.218758 3.37318

Average

120.00

100.00

60.00 Average

0.00 0 2 4 6 8 10 Normal Probability Plot

Y 100 0 0 20 40 60 80 100 120 Sample Percentile