On The Road To Logit And Probit Land

On the Road to Logit and Probit Land

Suppose we have a binary dependent variable and some covariate X1.

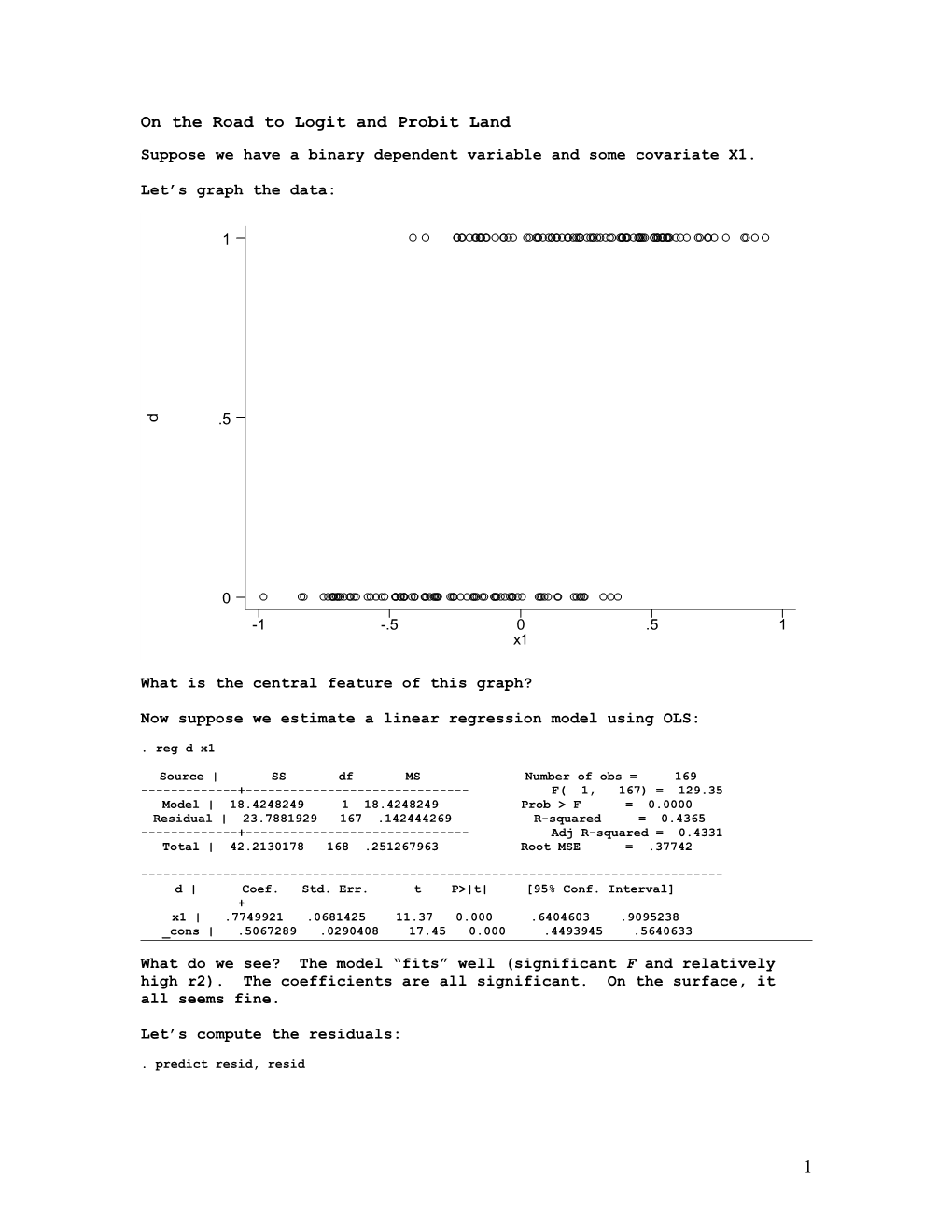
Let’s graph the data:

0 -1 -.5 0 .5 1 x1

What is the central feature of this graph?

Now suppose we estimate a linear regression model using OLS:

. reg d x1

Source | SS df MS Number of obs = 169 ------+------F( 1, 167) = 129.35 Model | 18.4248249 1 18.4248249 Prob > F = 0.0000 Residual | 23.7881929 167 .142444269 R-squared = 0.4365 ------+------Adj R-squared = 0.4331 Total | 42.2130178 168 .251267963 Root MSE = .37742

------d | Coef. Std. Err. t P>|t| [95% Conf. Interval] ------+------x1 | .7749921 .0681425 11.37 0.000 .6404603 .9095238 _cons | .5067289 .0290408 17.45 0.000 .4493945 .5640633

What do we see? The model “fits” well (significant F and relatively high r2). The coefficients are all significant. On the surface, it all seems fine.

Let’s compute the residuals:

. predict resid, resid

1 Now, let’s graph them (note I could use rvfplot command here if I wanted):

. gr resid x1, ylab xlab yline(0)

.5 s l a u d

i 0 s e R

-1 -1 -.5 0 .5 1 x1

What is the central feature of this graph? It illustrates the point that for any given X, there are 2 and only 2 possible values of e (the residual).

An implication of this is that the estimated variance of e will be heteroskedastic. One way to see this is to graph the squared residuals:

2 used intheOLSsetting. homoskedasticity. It heteroskedasticity, wewouldalwaysrejectthenullof Note thatifweperformedtheWhitetest(oranyotherfor X. Thisisendemictoheteroskedasticityproblems. Hmmmm…..it looksasifthevarianceofeissystematicallyrelatedto . grxbOLSx1,ylabxlabyline(0,1) and thengraphthem: (option xbassumed;fittedvalues) . predictxbOLS Let’s generatethepredictedvaluesfromourmodel: want tointerpretthesepredictionsasprobabilities. generate predictedvaluesonthedependentvariable.Further,wewould recommended!!) andproceededasusualwithOLS.Wemightwantto Suppose wedidn’tcareaboutheteroskedasticerrors(thoughthisisnot Squared Residuals .2 .4 .6 .8 0 -1 has tobethecaseforadichotomousd.v.when -.5 x1 0 .5 1 3 Fitted values d

-.5 -1 -.5 0 .5 1 x1

Oops. What is the central feature of this graph? There are several things to note, among them we find that when X is equal to -.98, the predicted probability is -.25. When X is equal to .94, the predicted probability is 1.23. One way to avoid this embarrassing problem is to place restrictions on the predicted values:

. gen xbOLSrestrict=xbOLS

. replace xbOLSrestrict=.01 if xbOLS<=0 (13 real changes made)

. replace xbOLSrestrict=.99 if xbOLS>=1 (10 real changes made)

Now, I’ll graph them:

. gr xbOLSrestrict d x1, ylab xlab yline(0,1)

4 xbOLSrestrict d

0 -1 -.5 0 .5 1 x1 Now, the problems are solved, sort of. We get valid predictions but only after post hoc restrictions on the predicted values. Gujarati and others discuss the LPM (using WLS). I will not (this is an easy model to estimate). Even with “corrections,” OLS is troublesome. What is another feature of the graph shown above?

The probabilities are assumed to increase linearly with X. The marginal effect of X is constant. Is this realistic? Unlikely.

What we would like is a model that produces valid probabilities (without post hoc constraints) and one where the probabilities are nonlinear in X. As Aldrich and Nelson (1984) [quoted in Gujarti] note, we want a model that “approaches zero at slower and slower rates as X gets small and approaches one at slower and slower rates as X gets very large.”

What we want is a sigmoid response function (or an “S-shaped” function). Note that all cumulative distribution functions are sigmoid response. Hence, if we use the CDF of a distribution to model the relationship between dichotomuous Y and X, we’ll resolve our problem. The question is: which CDF?

Conventionally, the logistic distribution and standard normal distribution are two candidates. The logistic gives rise to the logit model; the standard normal gives rise to the probit model.

For now, omit details of logit estimator. Let’s just estimate one and generate predicted values (which as we will see, are probabilities):

. logit d x1

Iteration 0: log likelihood = -117.0679

5 Iteration 1: log likelihood = -75.660879 Iteration 2: log likelihood = -71.457455 Iteration 3: log likelihood = -71.135961 Iteration 4: log likelihood = -71.132852 Iteration 5: log likelihood = -71.132852

Logit estimates Number of obs = 169 LR chi2(1) = 91.87 Prob > chi2 = 0.0000 Log likelihood = -71.132852 Pseudo R2 = 0.3924

------d | Coef. Std. Err. z P>|z| [95% Conf. Interval] ------+------x1 | 5.093696 .7544297 6.75 0.000 3.615041 6.572351 _cons | .0330345 .2093178 0.16 0.875 -.3772208 .4432898 ------

. predict xbLOGIT (option p assumed; Pr(d))

Now, let me graph them:

. gr xbLOGIT d x1, ylab xlab yline(0,1)

Pr(d) d

0 -1 -.5 0 .5 1 x1 What is the central feature of this graph?

Now, estimate probit and generate predicted values:

. probit d x1

Iteration 0: log likelihood = -117.0679 Iteration 1: log likelihood = -74.736867 Iteration 2: log likelihood = -70.555131 Iteration 3: log likelihood = -70.350158 Iteration 4: log likelihood = -70.349323

6 Probit estimates Number of obs = 169 LR chi2(1) = 93.44 Prob > chi2 = 0.0000 Log likelihood = -70.349323 Pseudo R2 = 0.3991

------d | Coef. Std. Err. z P>|z| [95% Conf. Interval] ------+------x1 | 3.056784 .4159952 7.35 0.000 2.241449 3.87212 _cons | .0189488 .1209436 0.16 0.876 -.2180963 .255994 ------

. drop xbprobit

. predict xbPROBIT (option p assumed; Pr(d))

. gr xbPROBIT d x1, ylab xlab yline(0,1)

Pr(d) d

0 -1 -.5 0 .5 1 x1 What is the central feature of this graph?

Differences between logit and probit?

7 Logit has“fatter”tails.Differenceisalmostalwaystrivial. d .5 0 1 -1 d Pr(d) -.5 x1 0 Pr(d) .5 1 8 Extensions: Logit Model

Illustrating Nonlinearity of Probabilities in Z.

Let’s reestimate model:

. logit d x1

Iteration 0: log likelihood = -117.0679 Iteration 1: log likelihood = -75.660879 Iteration 2: log likelihood = -71.457455 Iteration 3: log likelihood = -71.135961 Iteration 4: log likelihood = -71.132852 Iteration 5: log likelihood = -71.132852

Logit estimates Number of obs = 169 LR chi2(1) = 91.87 Prob > chi2 = 0.0000 Log likelihood = -71.132852 Pseudo R2 = 0.3924

------d | Coef. Std. Err. z P>|z| [95% Conf. Interval] ------+------x1 | 5.093696 .7544297 6.75 0.000 3.615041 6.572351 _cons | .0330345 .2093178 0.16 0.875 -.3772208 .4432898

Now, let’s generate “Z”.

. gen z=_b[_cons]+_b[x1]*x1

From z, let’s generate the logistic CDF (which is equivalent to P(Y=1):

One way to do it is like this:

. gen P=1/(1+exp(-z))

The other way to do it is like this:

. gen Prob=exp(z)/(1+exp(z))

Obviously, they’re equivalent statements (correlation is 1.0):

. corr P Prob (obs=169)

| P Prob ------+------P | 1.0000 Prob | 1.0000 1.0000

If we want to verify P is in the permissible range, then we can summarize Prob:

. summ Prob

Variable | Obs Mean Std. Dev. Min Max ------+------Prob | 169 .5147929 .3396981 .0069682 .9918078

Note that the probabilities range from .0069 to .99 (recall where the OLS probabilities fell).

Second, if we want to verify that P is nonlinearly related to Z, then we simply can graph P with respect to Z: gr Prob z, ylab xlab c(s)

9 . logitaff1white2ideo Now let’sturntosomerealdata: logit graphisthe This graphshouldlookfamiliar.Theonlydifferencebetweenthisandtheprevious Logit estimates Numberofobs= 2087 . logisticaff1white2ideo procedure:) We couldconvertcoefficientstooddsratios(Stata willdothisthroughthelogistic affirmative actionbutthatideologyispositively related. positive signsayslog-oddsincreasinginX.So we seewhitesarelesslikelytosupport Interpretation? Notnatural.Negativesigntell uslog-oddsaredecreasinginX; ------+------Log likelihood=-905.7173PseudoR20.1300 Logit estimatesNumberofobs=2087 Iteration 4:loglikelihood=-905.7173 Iteration 3:loglikelihood=-905.7173 Iteration 2:loglikelihood=-905.73209 Iteration 1:loglikelihood=-918.3425 Iteration 0:loglikelihood=-1041.0041

white2 |-1.837103.122431-15.010.000 -2.077063-1.597142 Prob _cons |-.1051663.0964957-1.090.276 -.2942944.0839618 ideo |.8629587.15080315.720.000 .567391.158527 aff1 |Coef.Std.Err.zP>|z| [95%Conf.Interval] .5 1 0 -5 X- Prob >chi2=0.0000 LR chi2(2)=270.57 axis. Hereitisz;beforewasX. 0 z 5 10 LR chi2(2) = 270.57 Prob > chi2 = 0.0000 Log likelihood = -905.7173 Pseudo R2 = 0.1300

------aff1 | Odds Ratio Std. Err. z P>|z| [95% Conf. Interval] ------+------white2 | .1592782 .0195006 -15.01 0.000 .1252976 .2024743 ideo | 2.370163 .357428 5.72 0.000 1.763658 3.185239

Odds ratios are nice. What about probabilities?

. predict plogit

Note: From this model I’ll get 14 probability estimates? Why?

. table plogit white2

------| white2 Pr(aff1) | 0 1 ------+------.0570423 | 48 .0750336 | 269 .097348 | 314 .1253988 | 830 .1600989 | 201 .2021813 | 165 .2536365 | 28 .2752544 | 13 .337441 | 42 .4037311 | 53 .4737326 | 326 .5447822 | 43 .6140543 | 43 .6808742 | 21

Generating probability scenarios:

. gen probscenario1=(exp(_b[_cons]+_b[white2]+_b[ideo]*ideo))/(1+(exp(_b[_cons] +_b[white2]+ _b[ideo]*ideo))) (68 missing values generated)

. gen probscenario2=(exp(_b[_cons]+_b[white2]*0+_b[ideo]*ideo))/(1+(exp(_b[_cons] +_b[white2]*0+_b[ideo]*ideo))) (68 missing values generated)

Now I have scenario for Whites and Nonwhites. I could graph them: gr probscenario1 probscenario2 ideo, ylab xlab b2(Ideology Scale) c(ll)

11 probscenario1 probscenario2

0 -1 -.5 0 .5 1 Ideology Scale

12 NOW, let’s turn to the PROBIT estimator. We reestimate our model.

. probit aff1 white2 ideo

Iteration 0: log likelihood = -1041.0041 Iteration 1: log likelihood = -906.32958 Iteration 2: log likelihood = -905.40724 Iteration 3: log likelihood = -905.40688

Probit estimates Number of obs = 2087 LR chi2(2) = 271.19 Prob > chi2 = 0.0000 Log likelihood = -905.40688 Pseudo R2 = 0.1303

------aff1 | Coef. Std. Err. z P>|z| [95% Conf. Interval] ------+------white2 | -1.081187 .0721158 -14.99 0.000 -1.222531 -.9398421 ideo | .4783113 .082473 5.80 0.000 .3166671 .6399554 _cons | -.0646902 .0598992 -1.08 0.280 -.1820905 .05271 ------

Note, the coefficients change. Why? A different CDF is applied.

Suppose we want to generate the utilities:

. gen U=_b[_cons]+_b[ideo]*ideo+_b[white2]*white2 (89 missing values generated)

. summ U

Variable | Obs Mean Std. Dev. Min Max ------+------U | 2396 -.9258217 .5063438 -1.624188 .413621

Note that they span 0: i.e. they are unconstrained (unlike the LPM).

Suppose we want to compute probabilities?

We can take our function:

. gen Prob_U=norm(U) (89 missing values generated)

. summ Prob_U

Variable | Obs Mean Std. Dev. Min Max ------+------Prob_U | 2396 .2034129 .1554985 .0521678 .6604242

What have I done here? (I’ve used Stata’s function for the normal distribution: i.e. the CDF for the Normal).

Of course, I could ask Stata to compute these directly:

. predict probitprob (option p assumed; Pr(aff1)) (89 missing values generated)

You can verify for yourself that what I type before is equivalent to the Stata predictions.

Note that as with logit, we will only get 14 probabilities (why?)

13 . table probitprob white2

------| white2 Pr(aff1) | 0 1 ------+------.0521678 | 48 .0719306 | 269 .0961646 | 314 .1259231 | 830 .161568 | 201 .2032153 | 165 .2522055 | 28 .2935644 | 13 .3518333 | 42 .4119495 | 53 .4742103 | 326 .5371088 | 43 .5990911 | 43 .6604242 | 21

Comparison of probabilities? Let’s correlate the logit with the probit probs:

. corr probitprob plogit (obs=2396)

| probit~b plogit ------+------probitprob | 1.0000 plogit | 0.9996 1.0000

Effectively, no difference.

Note that as with logit, we can generate probability scenarios:

. gen prob1=norm(_b[_cons]+_b[white2]+_b[ideo]*ideo) (68 missing values generated)

. gen prob2=norm(_b[_cons]+_b[white2]*0+_b[ideo]*ideo) (68 missing values generated)

The only difference is we use the standard normal CDF to derive the function.

14 Illustrating Likelihood Ratio Test

Using results from Probit Model:

Here, I compute –2logLo-(-2logLc)

. display (-2*-1041.0041)-(-2*-905.40688) 271.19444

This is equivalent to –2(logLo-logLc)

. display -2*(-1041.0041--905.40688)

271.19444

This is what Stata reports as “LR chi2(2)”. The (2) denotes there are k=2 degrees of freedom.

Let’s illustrate this on a case where an independent variable is not significantly different from 0. I generate a random set of numbers and run my probit model:

. set seed 954265252265262626262

. gen random=uniform()

. probit aff1 random

Iteration 0: log likelihood = -1077.9585 Iteration 1: log likelihood = -1077.9214

------aff1 | Coef. Std. Err. z P>|z| [95% Conf. Interval] ------+------random | -.0290269 .106446 -0.27 0.785 -.2376571 .1796033 _cons | -.8227274 .0616407 -13.35 0.000 -.9435409 -.7019139 ------

Here, the LR test is given by –2(-1077.9585—1077.9214) which is

. display -2*(-1077.9585--1077.9214) .0742

Using Stata as chi2 table, I find that the p-value for this test statistic is equal to:

. display chi2tail(1,.0742) .78531696

Which clearly demonstrates that the addition of the covariate “random” adds nothing to this model.

Now, let’s illustrate another kind of LR test.

We reestimate the “full” probit model.

Iteration 0: log likelihood = -1041.0041 Iteration 1: log likelihood = -906.32958 Iteration 2: log likelihood = -905.40724

15 Iteration 3: log likelihood = -905.40688

------aff1 | Coef. Std. Err. z P>|z| [95% Conf. Interval] ------+------white2 | -1.081187 .0721158 -14.99 0.000 -1.222531 -.9398421 ideo | .4783113 .082473 5.80 0.000 .3166671 .6399554 _cons | -.0646902 .0598992 -1.08 0.280 -.1820905 .05271 ------

Now, let’s reestimate a simpler model:

. probit aff1 white2 if ideo~=.

Iteration 0: log likelihood = -1041.0041 Iteration 1: log likelihood = -922.93117 Iteration 2: log likelihood = -922.53588 Iteration 3: log likelihood = -922.53587

------aff1 | Coef. Std. Err. z P>|z| [95% Conf. Interval] ------+------white2 | -1.09842 .0716505 -15.33 0.000 -1.238852 -.9579877 _cons | -.0567415 .059649 -0.95 0.341 -.1736513 .0601683 ------

(Why is the “if” command used?)

The difference in the model chi2 between the first and second models can be used to evaluate whether or not the addition of the “ideology” covariate adds anything.

For the first model (call it M0), we see the model chi2 is 271.19 and for the second model (call it M1), the model chi2 is 236.94.

The difference then is MO-M1 or 271.19-236.94=34.25. On 1 degree of freedom, we see the p-value is:

. display chi2tail(1, 34.25) 4.847e-09 which clearly shows the addition of the ideology covariate improves the fit of the model.

There is a simpler way to do this. Stata has a command called lrtest which can be applied to any model that reports log-likelihoods. The command works by first estimating the “full” model and then estimating the “simpler” or reduced model. To illustrate, let me reestimate M0 (I’ll suppress the output)

[output suppressed]

Next I type:

. lrtest, saving(0)

Then I estimate my simpler model:

16 . probit aff1 white2 if ideo~=.

[output suppressed].

Next I type:

. lrtest, saving(1)

Now I have two model chi2 statistics saved: one for M0 and one for M1. To compute the likelihood ratio test I type:

. lrtest Probit: likelihood-ratio test chi2(1) = 34.26 Prob > chi2 = 0.0000

Compare this to my results from above. They are identical (as they should be).