Achievement Standard 3.4 Homework Assignment

Question One

Solve the system of equations:

-x + z = - 1 2x - y = 8 2y + 10 = 3z

Question Two

The equation 2x3 – 3x2 – 36 = 0 has a solution between x = 3 and x = 4.

Find an approximation of the root of f(x) = 0 either by obtaining three iterates using the Newton-Raphson method with x = 3.5 as the starting value, AND by obtaining three iterates using the bisection method with x = 3 and x = 4 as the starting values.

Show all steps in your working clearly.

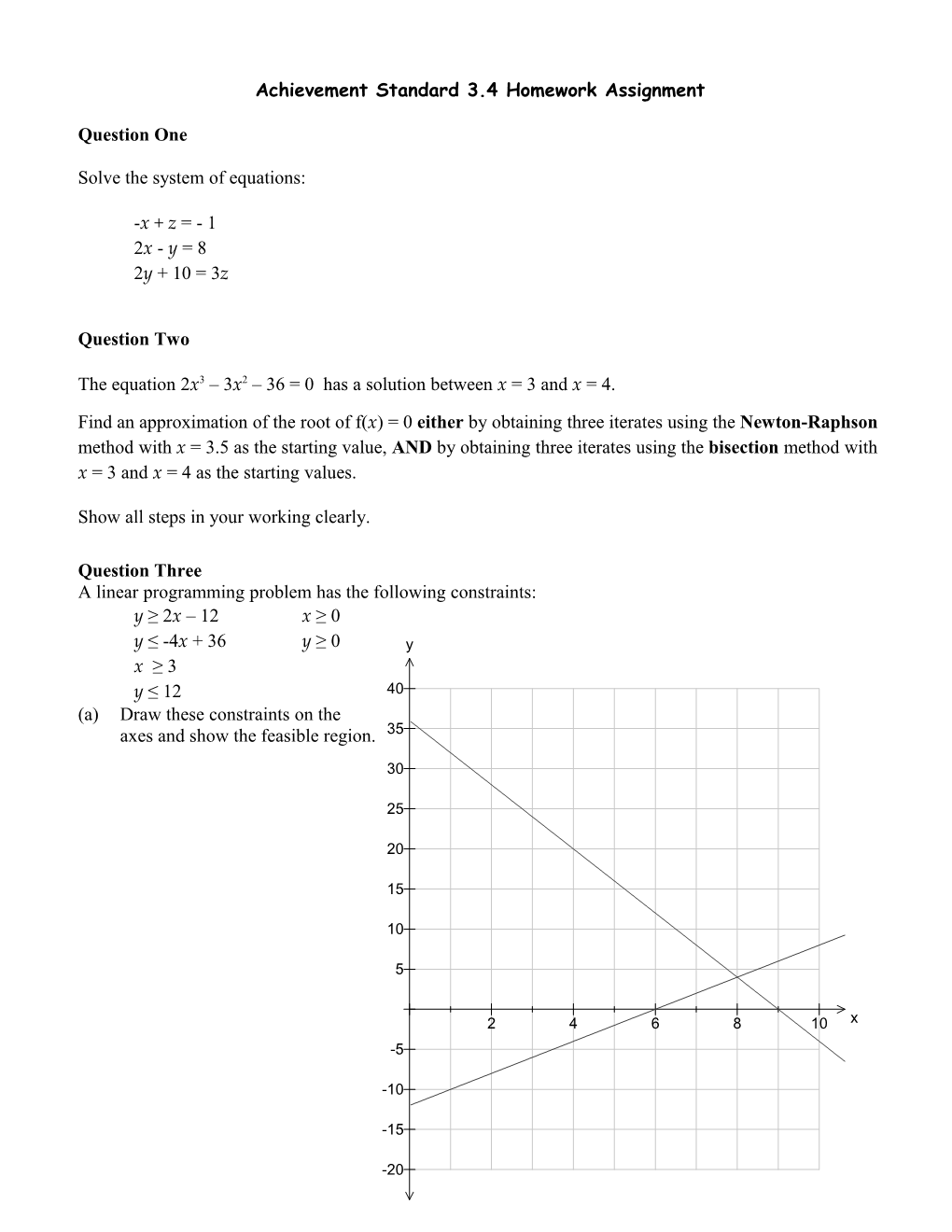
Question Three A linear programming problem has the following constraints: y ≥ 2x – 12 x ≥ 0 y ≤ -4x + 36 y ≥ 0 y x ≥ 3 y ≤ 12 40 (a) Draw these constraints on the axes and show the feasible region. 35

2 4 6 8 10 x -5

-20 b) Find the values of x and y which maximise the objective function P = 3x + 2y subject to the constraints.

Question Four Sarah has set up a training programme to prepare herself for a major triathlon competition. The training programme involves cycling, swimming and running. The table below gives the time (minutes) Sarah spent at each activity and the total number of kilojoules she burned from the day’s training, for three days of her programme.

Total no. Cycling Swimming Running kilojoules Day one 60 60 30 7.54 Day two 90 45 60 10.65 Day three 120 0 120 14.80

Set up and solve a system of equations to find the number of kilojoules of energy Sarah burns per hour from each type of activity. 123456– 1 01. 123456789 Question Five A student needed to find the point where the line y = 3x - 2 intersected with the curve 2 y  to solve a problem she was attempting. x 2

y 6 5 4 3 2 1

0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1 1.1 1.2 1.3 x – 1

In order to solve the problem she needs to solve the equation 3x3 – 2x2 – 2 = 0.

Use the bisection method AND the Newton-Raphson method to find an approximation to the root of the equation. Show three iterations for the bisection method and give your answer correct to two decimal places for the Newto-Raphson method.

You must clearly show how you established your starting value(s) and the result for each iteration. Question Six Samantha has been chosen for the New Zealand Under-17 World Cup Soccer squad for the tournament to be held in New Zealand in 2008. Part of the squad training involves camps to be held both in New Zealand and overseas. Samantha has to raise a considerable amount of money to attend these camps if she is to realize her ambition to play for New Zealand at the tournament.

Part of her fundraising initiative is to sell bundles of toilet tissue and paper towels. Samantha only has enough room to store a maximum of 65 bundles of toilet tissue or paper towels (in total) but she already has orders for 10 bundles of each of the toilet tissue and paper towels. Sam also has a limit of $800 to spend on purchasing her stock. The toilet tissue costs $16 per bundle, while the paper towels cost $10 per bundle.

Samantha will sell the toilet tissue for $8 profit per bundle and the paper towels for $6 profit per bundle.

(a) Write down the constraints you need in order to calculate the number of bundles of toilet tissue and the number of bundles of paper towels Samantha should purchase to maximise her profit.

(b) Assuming Samantha sells all the stock she purchases how many bundles of each should she purchase in order to maximise her profit.

10 20 30 40 50 60 70 80 90 100 x (c) When Samantha goes to purchase her stock she is told that the price she hopes to get for the paper towels is a bit high and she is not likely to sell them very easily at that price. She decides to reduce her price by $1 per bundle.

How many of each type of bundle should Samantha now purchase to sell, again assuming she will sell all she purchases?

Question Seven Consider the following system of equations.

2x + 6y + 2z = 20 4x + 2y - z = 50 -x + y + z = 20

Give a geometrical description of how the planes represented by these three equations relate to each other.

Question Eight The equation f (x)  3e 2x  2x 2  2  0 is to be solved for x. When finding integer values surrounding the root Ben generates the following table of values and assumes there is no root in the interval from x = -1 to x = 2.

x -1 0 1 2 f(x) 22.2 1 0.4 6.1 (a) Explain why Ben has made an incorrect conclusion (b) Show that there is a root to the equation f (x)  3e2x  2x2  2  0 between x = 0.5 and 1.0.

(c) Use the graph to show geometrically how the first two iterates, x1 and x2, are found using the

Newton-Raphson method. Use x0 = 0.7. (Note: f (x)  6e 2x  4x but you are not required to calculate exact value).