Stuff I Need to Know for Econ 15B

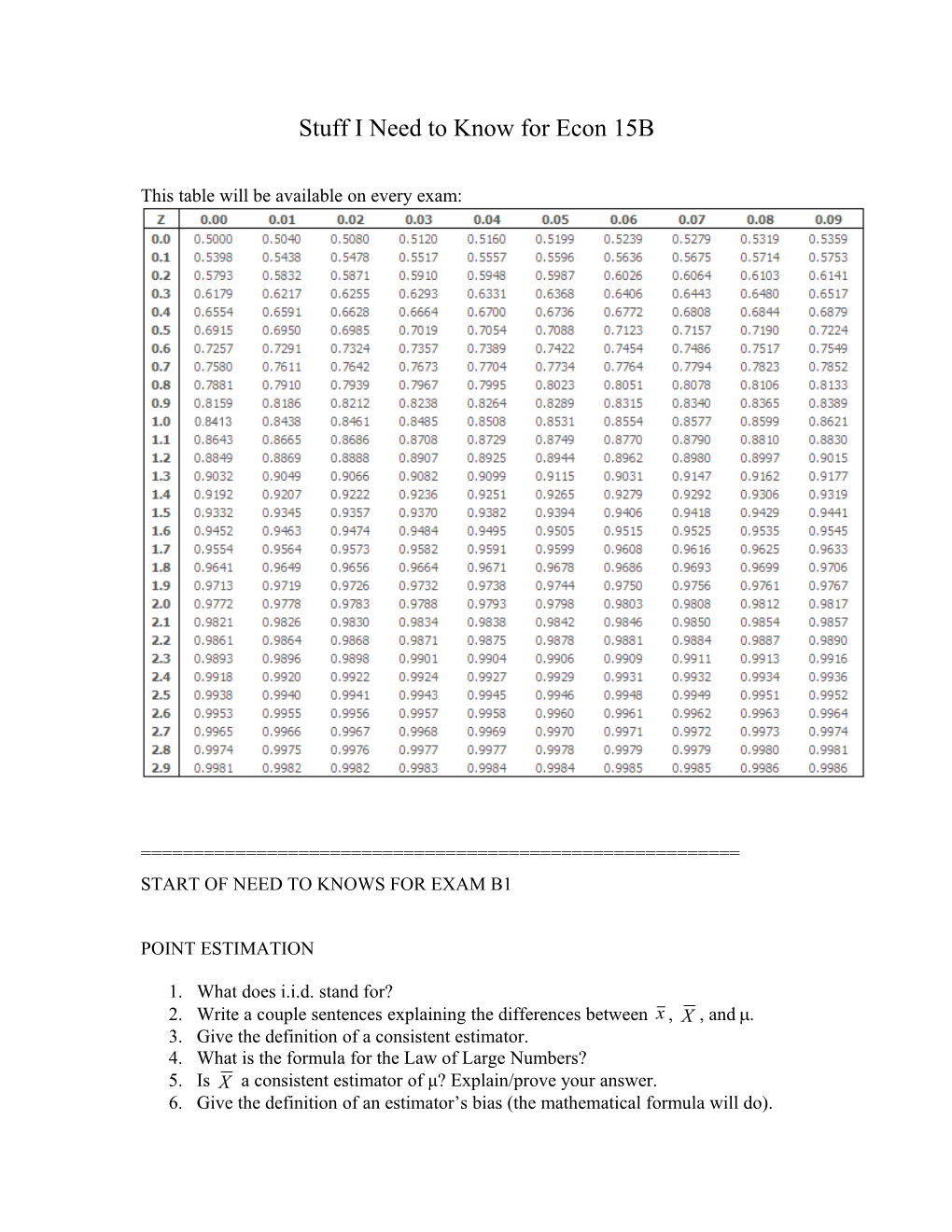
This table will be available on every exam:

======START OF NEED TO KNOWS FOR EXAM B1

POINT ESTIMATION

1. What does i.i.d. stand for? 2. Write a couple sentences explaining the differences between x , X , and  3. Give the definition of a consistent estimator. 4. What is the formula for the Law of Large Numbers? 5. Is X a consistent estimator of μ? Explain/prove your answer. 6. Give the definition of an estimator’s bias (the mathematical formula will do). 7. Give the definition of a biased estimator (the mathematical formula will do). 8. Give the definition of an unbiased estimator (the mathematical formula will do). 9. Show that (i.e., calculate, like we did in class) X is an unbiased estimator of . 10. Calculate an unbiased estimate of 2 using the random sample {2, 1, -3, 1}. 11. Calculate an estimate of  (using an unbiased estimate of 2) from the random sample {2, 1, -3, 1}. 12. Calculate s from the data set {3, -1, 4, 5, 0}. 13. Calculate s2 from the data set {3, -1, 4, 5, 0}.

14. Calculate sx from the data set {3, -1, 4, 5, 0}. 2 15. Calculate sx from the data set {3, -1, 4, 5, 0}.  16. Do the calculations to show that   X n 17. If a random sample of 15 Xs come from a distribution with a variance of 6, then what is the variance of X ? 18. If a random sample of 15 Xs come from a distribution with a variance of 6, then what is the standard deviation of X ? 19. If a random sample of 15 Xs come from a distribution with a standard deviation of 6, then what is the variance of X ? 20. If a random sample of 15 Xs come from a distribution with a standard deviation of 6, then what is the standard deviation of X ? 21. In general, if we have a random sample of n Xs from a distribution whose mean and standard deviation is  and , then what is the mean and standard deviation of X ? n 2 1 2 22. Is X i  X  an unbiased estimator of  ? If not, give its bias. n i1 n 1 2 2 23. If  = 35, and n = 12, calculate the bias of X i  X  . n i1 24. As part of a proof that S2 is an unbiased estimator of 2, show that: n n n n 2 2 2 å(X i - X ) = å(Xi - m) + å(X - m) - 2å(Xi - m)(X - m) i=1 i=1 i=1 i=1 25. As part of a proof that S2 is an unbiased estimator of 2, show that: é n ù 2 E ê2 å(X i - m)(X - m)ú = 2s ë i=1 û 26. As part of a proof that S2 is an unbiased estimator of 2, show that: é n ù 2 2 E êå (X i - m) ú = ns ë i=1 û 27. As part of a proof that S2 is an unbiased estimator of 2, show that: n é 2 ù E êå (X - m) ú = s 2 ë i=1 û 28. Use the previous four equations to calculate that S2 is an unbiased estimator of 2.

29. Your colleague at work was gathering some data for you, and you noticed that she accidentally estimated the standard deviation as the square root of the average of the sum of the squared deviations from the sample mean (i.e., she "divided by n"). Her estimate was 270 for the 15 observations she collected. You wish to use an unbiased estimate of the sample variance. What is it (show your work)? 30. Give the formula for S2. Why do we use this estimator? 31. What is a point estimate? How is it different from a point estimator and from a population parameter? 32. What is a point estimator? How is it different from a point estimate and from a population parameter? 33. What is a population parameter? How is it different from a point estimate and from a point estimator?

34. Calculate the value of E(X ) in terms of the mean  of Xi, (i.e., like we did in class). 2 35. Calculate the variance of X in terms of the variance  of Xi (i.e., like we did in class). 36. If {X1,…, X37} is a random sample from N(100, 25), then what is the variance of X ? 37. If {X1,…, X37} is a random sample from N(100, 25), then what is the standard deviation of X ? X - m 38. Suppose X has a mean μ and standard deviation σ; let Z = . Calculate the s mean of Z, using the linearity of expectations. X - m 39. Suppose X has a mean μ and standard deviation σ; let Z = . Calculate the s standard deviation of Z, using the linearity of expectations.

THE NORMAL DISTRIBUTION AND THE CLT

40. For Z~N(0,1), use the table above to estimate Pr[Z ≤ 1.8] 41. For Z~N(0,1), use the table above to estimate Pr[Z > 2.2] 42. For Z~N(0,1), use the table above to estimate Pr[-.2 < Z < .8] 43. For X ~ N(25, 18), use the table above to estimate Pr[X ≤ 31] 44. For X ~ N(25, 18), use the table above to estimate Pr[X > 22] 45. For X ~ N(25, 18), use the table above to estimate Pr[22 < X ≤ 30]] 46. For Z~N(0,1), what is the z such that Pr[Z ≤ z] = .93? 47. For Z~N(0,1), what is the z such that Pr[Z > z] = .94? 48. For Z~N(0,1), what is the z such that Pr[Z > z] = .03? 49. For Z~N(0,1), what is the z such that Pr[Z ≤ z] = .04? 50. For Z~N(0,1), what is the z such that Pr[-z ≤ Z < z] = .94? 51. For X~N(4,7), what is the x such that Pr[X ≤ x] = .93? 52. For X~N(4,7), what is the x such that Pr[X > x] = .94? 53. For X~N(4,7), what is the x such that Pr[X > x] = .03? 54. For X~N(4,7), what is the x such that Pr[X ≤ x] = .04? 55. For X~N(4,7), what are the xL and xU that are equidistant from the mean, and such that Pr[xL < X ≤ xU] = .94? 56. Many test scores are (approximately) normally distributed. Your professor reports that the midterm average was a 78, and that the standard deviation was 8. You got an 88 on the midterm. Approximately what percentile does that put you in? (I.e., what percentage of the students did you score higher than?) 57. Many test scores are (approximately) normally distributed. Your professor reports that the midterm average was a 78, and that the standard deviation was 8. What is the approximate range of scores for the middle 50% of the scores? 58. Many test scores are (approximately) normally distributed. Your professor reports that the midterm average was a 78, and that the standard deviation was 8. What is the approximate range of scores for the top 10% of the scores? 59. Many test scores are (approximately) normally distributed. Your professor reports that the midterm average was a 78, and that the standard deviation was 8. What is the approximate range of scores for the bottom 10% of the scores? 60. What is the value of (0)? 61. Suppose X ~ N(0, 1). Which, if either, is more likely: .3 ≤ X ≤ .4, or .7 ≤ X ≤ .8? Explain your answer (you do not need to calculate these values). 62. Suppose X ~ N(0, 1). Which, if either, is more likely: –1 ≤ X ≤ 1, or 5 ≤ X ≤ 10? Explain your answer (you do not need to calculate these values). 63. Draw and label the graphs of the pdf (together, on one set of axes) of N(0,1) and N(-1, 2). Your graphs should display how the different parameters of the two distributions affect the pdfs. 64. What is the total area under the curve of the pdf of N(0, 1)? 65. What is E[X] if X ~ N(, 2)? 66. What is E[X] if X ~ N(1, 3)? 67. What is the mean of X if X ~ N(, 2)? 68. What is the variance of X if X ~ N(, 2)? 69. What is the standard deviation of X if X ~ N(, 2)? 70. What is the mean of X if X ~ N(1, 3)? 71. What is the variance of X if X ~ N(1, 3)? 72. What is the standard deviation of X if X ~ N(1, 3)? 73. What is  of X if X ~ N(1, 3)? 74. What is 2 of X if X ~ N(1, 3)? 75. What is  of X if X ~ N(1, 3)? 76. What is E[(X – E[X])2] if X ~ N(, 2)? 77. What is E[(X – E[X])2] if X ~ N(, )? 78. What is the (standardized) skew of N(, 2)? 79. What is the (standardized) kurtosis of N(, 2) (or: if your answer to this is 0, then what constant number is subtracted from the formula to yield 0)? 80. For N(, 2), calculate the largest value of its pdf. Show also that any other value – i.e. x = μ+c, (c ≠ 0) – will be less than this number. 81. If X ~ N(0, 1), then what is the distribution of Y = a + bX (b ≠ 0)? 82. If X ~ N(, 2), how would you transform it so that it is distributed as N(0, 1)? 83. If X ~ N(, 2), then what is the distribution of Y = a + bX (b ≠ 0)? 84. If X ~ N(0, 1), then what is the distribution of Y = 2 + 3X? 85. If X ~ N(, ), how would you transform it so that it is distributed as N(0, 1)? 86. If X ~ N(, ), then what is the distribution of Y = 2 + 3X? 87. What background conditions must hold in order for the Central Limit Theorem to hold? 88. Give the limit formula in the Central Limit Theorem as a limit formula of a sum of standardized random variables (scaled by n-1/2). In this formula, what random variables are being standardized? 89. Give the limit formula in the Central Limit Theorem as a limit formula of a standardization of a single random variable. In this formulation, what random variable is being standardized? 90. Show that the two forms of the Central Limit Theorem are equivalent by 1 n  X    X   calculating that:  i   n i1     X 91. The host probability distribution (e.g., wages of individuals) whose mean you wish to estimate is not normally distributed, and yet your analysis of the mean of a random sample involves the normal distribution. Explain why. 92. If a data set {1, 2, 5, 7, 2} is a random sample from a distribution where  = 4, and  = 3, what is the z-score for x ? 93. If a data set {1, 2, 5, 7, 2} is a random sample from a distribution where  = 4, and  = 7, what is the z-score for x ?

BASIC CONFIDENCE INTERVALS

94. Give the formula for the margin of error (when the variance is known). 95. Give the formula for a confidence interval in terms of the point estimate and the margin of error. 96. What is the formula for the lower bound of a confidence interval when the variance is known? Label the parts (do not just give the m.o.e. as a single part). 97. What is the formula for the upper bound of a confidence interval when the variance is known? Label the parts (do not just give the m.o.e. as a single part). 98. When the variance is known, what probability distribution do we refer to when constructing a confidence interval for the mean? 99. In constructing confidence intervals, it is utterly critical that the event X   1 1  q   q is the same thing as X  q    X  q . Do the  X n n calculations to show that these two events are indeed the same (like we did in class). 100. What are the boundaries of a confidence interval at the .99 confidence level if the variance in the 14 samples is known to be 6, and the sample mean was 8? 101. Calculate a 99% confidence interval for a data set of 14 observations, whose mean is 6.2, and whose variance is known to be 7. 102. Calculate a 99% confidence interval for a data set of 14 observations, whose mean is 6.2, and whose standard deviation is known to be 7. 103. Calculate a 95% confidence interval for the data set {3, 5, 2, 1, 3}. Treat your estimate of the variance as if it were known to be the true variance. 104. For a given data set, which is larger, the length of a 95% confidence interval, or the length of a 99% confidence interval? Explain your answer. 105. Suppose two data sets x and y have identical means and variances, but x is made up of 17 observations, and y contains 20. Which will have a larger confidence interval? Explain your answer.

106. Draw the graph of the pdf for N(0,1); label the x-axis on the graph corresponding to the probabilities: .005, .025, .05, .5, .95, .975, and .995. (Give the axis values, not the (cdf) probabilities themselves.) 107. Draw the graphs of the pdf for N(μ, σ2). Label the x-axis points corresponding to the values: μ – 2σ, μ – σ, μ, μ + σ, and μ + 2σ. 108. On one set of axes, draw the graphs of the pdfs for N(1, 2) and N(-2, 1). For both functions, label the x-axis points corresponding to the probabilities .025, 1/6, .5, 5/6, and .975. (Give the axis values, not the (cdf) probabilities themselves.) 109. On one set of axes, draw the graphs of the pdfs for N(1, 2) and N(-2, 1). For both functions, label the x-axis points corresponding to the values: μ – 2σ, μ – σ, μ, μ + σ, and μ + 2σ.

110. The firm you work for has a rather poorly-thought-out policy that any estimations of the cost of a certain activity must be within a margin of error of no more than ± 10% of the estimated cost. (The company doesn’t care about the confidence level of the margin of error, only that it be such that the above rule is upheld.) A project that you’re working on has an average cost of $10,000, which was derived from a sample of all 11 known observations with a known standard deviation of 1,869. To comply with your company’s policy, what is the highest confidence level you may use to construct this margin of error? (Estimate this by using the chart above to give the two points which it must fall in between, or the extreme point if it is greater/less than all those given.) 111. You work in an IT firm that specializes in a certain sort of information retrieval for corporations. Your boss has assigned you the task of estimating how long a certain sort of advanced retrieval takes on average. Since a major business is seriously considering an account with your company, your boss wants you to be “99 percent sure” that your estimate falls within a 10-point total spread that you will give him. The variance of these sorts of retrievals is known to be 4800. What is the least number of trials of the system that you would have to run to complete your task (using the techniques that this test covers)? 112. Assuming  is known, how many times larger will your margin of error be if you switch from a 95% to 99% confidence level (show your work)? 113. Assuming  is known, how many times larger will the length of your confidence interval be if you switch from a 90% to a 95% confidence level (show your work)? 114. If your original sample size is n, how much larger must you make your sample size if you want your margin of error to be cut in half (assume all other quantities remain fixed)? 115. If your original sample size is 30, how large must your new sample size be if you want your margin of error to be only half its original size (assume all other quantities remain fixed)? 116. In a given study, how (if at all) would increasing the size of x affect the margin of error? 117. In a given study, how (if at all) would increasing the size of x affect the upper and lower bounds of a confidence interval? 118. In a given study, how (if at all) would increasing the size of x affect the length of a confidence interval? 119. In a given study, how (if at all) would increasing the size of  affect the margin of error? 120. In a given study, how would increasing the size of  affect the upper and lower bounds of a confidence interval? 121. In a given study, how (if at all) would increasing the size of  affect the length of a confidence interval? 122. In a given study, how (if at all) would increasing the size of n affect the margin of error? 123. In a given study, how (if at all) would increasing the size of n affect the upper and lower bounds of a confidence interval? 124. In a given study, how (if at all) would increasing the size of n affect the length of a confidence interval? 125. In a given study, how (if at all) would increasing the size of the confidence level c affect the margin of error? 126. In a given study, how (if at all) would increasing the size of the confidence level c affect the upper and lower bounds of a confidence interval? 127. In a given study, how (if at all) would increasing the size of the confidence level c affect the length of a confidence interval? 128. In a given study, how (if at all) would increasing the size of the error probability  affect the margin of error? 129. In a given study, how (if at all) would increasing the size of the error probability  affect the upper and lower bounds of a confidence interval? 130. In a given study, how (if at all) would increasing the size of the error probability  affect the length of a confidence interval? 131. In estimating the mean of X, the size of your 94% margin of error was (approximately) 7. What is the (approximate) size of n if the known standard deviation of X is 3? 132. In estimating the mean of X, your 94% confidence interval had a total length of (approximately) 7. What is the (approximate) size of n if the known standard deviation of X is 3? 133. In estimating the mean of X (where X has a known standard deviation of 5), the size of your 94% margin of error was (approximately) 7. What is the size of the margin of error if you change the confidence level to 98%? 134. In estimating the mean of X (where X has a known standard deviation of 5), your 94% confidence interval had a total length of (approximately) 7. What is the length of the confidence interval if you change the confidence level to 98%? 135. If you have two data sets that yield identical estimates of the variance, but for the first one you used 20 observations and for the second you used 30, which one will have the larger margin of error? Calculate/explain/prove your answer. 136. Describe the role that the Central Limit Theorem plays in our construction of confidence intervals. 137. Construct a margin of error (at the 94% confidence level) for the mean for the data set {3, 2, -2, 0}. 138. If the length of my confidence interval is 8, how long is it if I double the size of my data (assume all other quantities remain the same)? 139. If my margin of error is 5, what is it if I double the size of my data (assume all other quantities remain the same)? 140. If my margin of error is 5, how long is my confidence interval if I double the size of my data (assume all other quantities remain the same)? 141. If my margin of error is 5, what is the length of my confidence interval? 142. If the length of my confidence interval is 9, what is my margin of error? 143. When estimating the mean of a probability distribution of some population of interest (variance known), a confidence interval is typically constructed using a normal distribution, even if the underlying population distribution is not normal. Why is this done? 144. A report gives a point estimate of 156.78 with a margin of error of 23.42. What is the corresponding confidence interval? 145. A report gives a confidence interval of (223.83, 325.76). What are x and the margin of error?

T-DISTRIBUTION CIs 146. What is the formula for the lower bound of a confidence interval when the variance is unknown? Label the parts – do not simply specify the margin of error; give that in terms of its parts and label them. 147. What is the formula for the upper bound of a confidence interval when the variance is unknown? Label the parts – do not simply specify the margin of error; give that in terms of its parts and label them. 148. What is the formula for the margin of error when the variance is unknown? Label the parts 149. When the variance is unknown, what distribution do we refer to when constructing a confidence interval for the mean, when the sample has 18 observations in it? 150. What additional uncertainty does the t-distribution account for that the normal distribution does not? 151. If you are using student’s T distribution with 11 degrees of freedom, how large was your sample? 152. For a given data set you construct 99% confidence intervals using first the standard normal distribution, and then using the appropriate t-distribution. Which confidence interval is longer, and why? 153. Sketch the graphs of the pdfs of N(0, 1) and T(5) on one set of axes. Label each graph, and for each graph, numerically label (i) the means, and those points that are (roughly) (ii) 1 standard deviation from the mean, and (iii) 2 standard deviations from the mean. 154. Sketch the graphs of the pdfs of T(35) and T(5) on one set of axes. Label each graph, and for each graph, numerically label (i) the means, and those points that are (roughly) (ii) 1 standard deviation from the mean, and (iii) 2 standard deviations from the mean.

END OF NEED TO KNOWS FOR EXAM B1

======