Time Series, Forecasting, and Index Numbers

CHAPTER 12 TIME SERIES, FORECASTING, AND INDEX NUMBERS

12-1. Trend analysis is a quick method of determining in which general direction the data are moving through time. The method lacks, however, the theoretical justification of regression analysis because of the inherent autocorrelations and the intended use of the method in extrapolation beyond the estimation data set.

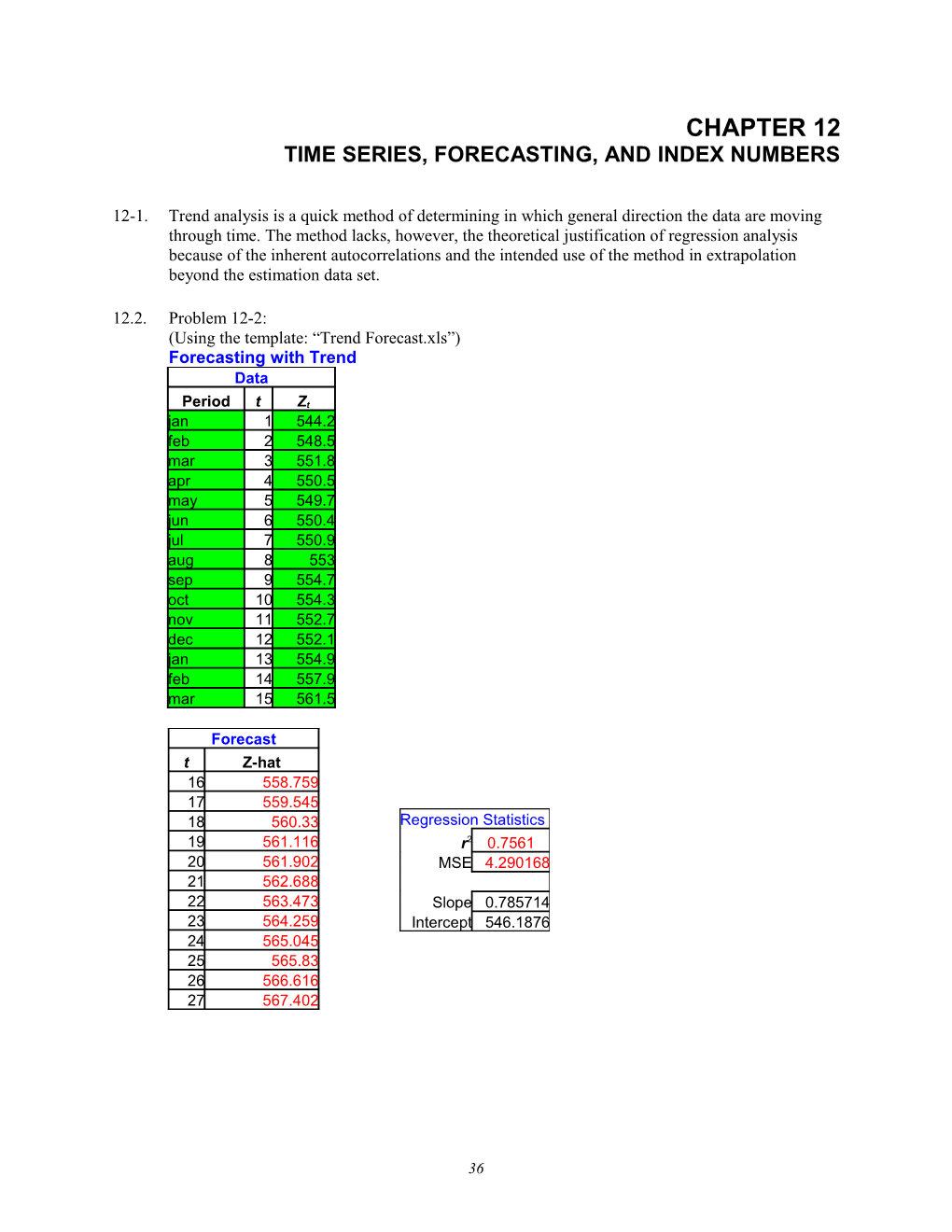
12.2. Problem 12-2: (Using the template: “Trend Forecast.xls”) Forecasting with Trend Data

Period t Zt jan 1 544.2 feb 2 548.5 mar 3 551.8 apr 4 550.5 may 5 549.7 jun 6 550.4 jul 7 550.9 aug 8 553 sep 9 554.7 oct 10 554.3 nov 11 552.7 dec 12 552.1 jan 13 554.9 feb 14 557.9 mar 15 561.5

Forecast t Z-hat 16 558.759 17 559.545 18 560.33 Regression Statistics 19 561.116 r2 0.7561 20 561.902 MSE 4.290168 21 562.688 22 563.473 Slope 0.785714 23 564.259 Intercept 546.1876 24 565.045 25 565.83 26 566.616 27 567.402

36 Forecast for April, 2004 = 558.8

12-3. The trend regression is: 2 b0 = 34.818 b1 = 12.566 r = .9858 yˆ (2005) = 198.182 yˆ (2006) = 210.748 (Using the template: “Trend Forecast.xls”) Forecasting with Trend Data

Period t Zt 1993 1 53 1994 2 65 1995 3 74 1996 4 85 1997 5 92 1998 6 105 1999 7 120 2000 8 128 2001 9 144 2002 10 158 2003 11 179 2004 12 195

Forecast t Z-hat 13 198.182 14 210.748 15 223.315 16 235.881 17 248.448 18 261.014 19 273.58 20 286.147 Regression Statistics 21 298.713 r2 0.9858 22 311.28 MSE 32.51189 23 323.846 24 336.413 Slope 12.56643 Intercept 34.81818

Forecast for 2005 = 198.182 and for 2006 = 210.748

37 12-4. Trend model through 2000

Forecast t Z-hat 25 1.63623 26 1.64622 27 1.6562 28 1.66619 29 1.67617 30 1.68616 31 1.69614 32 1.70613 33 1.71611 34 1.7261 35 1.73608 36 1.74607

Comparison to 2001: (not available when Solutions Manual written)

12-5. No, because of the seasonality.

12-6. No. Cyclicity is not well modeled by trend analysis.

12-7. The term, ‘seasonal variation’ is reserved for variation with a cycle of one year.

12-8. There will be too few degrees of freedom for error.

12-9. The weather, for one thing, changes from year to year. Thus sales of winter clothing, as an example, would have a variable seasonal component.

12.10. Beer sales at a local establishment, as an example: high during weekend nights, low at other times.

38 12.11. Using a computer: Linear regression trend line: Zhat(t) = 372.876 + 0.8896 t

Centered C(t) = Ratio Seasonal [Desea- data: trend: Moving CMA Moving Index soned] `t (mon.) Z(t) Zhat(t) Average Zhat(t) Average S Z(t)/S%

1 (Jun) 375.00 373.77 99.52 376.83 2 (Jul) 370.00 374.66 98.87 374.22 3 (Aug) 374.00 375.54 99.25 376.82 4 (Sep) 378.00 376.43 99.74 378.97 5 (Oct) 376.00 377.32 99.78 376.82 6 (Nov) 380.00 378.21 100.48 378.20 7 (Dec) 384.00 379.10 378.62 0.999 101.42 102.33 375.26 8 (Jan) 380.00 379.99 379.37 0.998 100.16 100.95 376.43 9 (Feb) 378.00 380.88 380.29 0.998 99.40 99.84 378.62 10 (Mar) 380.00 381.77 381.12 0.998 99.70 99.39 382.31 11 (Apr) 382.00 382.66 382.08 0.998 99.98 100.09 381.64 12 (May) 383.00 383.55 383.17 0.999 99.96 99.76 383.92 13 (Jun) 382.00 384.44 384.46 1.000 99.36 99.52 383.86 14 (Jul) 381.00 385.33 386.00 1.002 98.70 98.87 385.35 15 (Aug) 385.00 386.22 387.37 1.003 99.39 99.25 387.91 16 (Sep) 387.00 387.11 388.37 1.003 99.65 99.74 387.99 17 (Oct) 390.00 388.00 389.25 1.003 100.19 99.78 390.85 18 (Nov) 392.00 388.89 390.12 1.003 100.48 100.48 390.14 19 (Dec) 403.00 389.78 390.96 1.003 103.08 102.33 393.82 20 (Jan) 398.00 390.67 391.83 1.003 101.57 100.95 394.26 21 (Feb) 393.00 391.56 392.54 1.003 100.12 99.84 393.65 22 (Mar) 389.00 392.45 393.21 1.002 98.93 99.39 391.37 23 (Apr) 394.00 393.34 393.79 1.001 100.05 100.09 393.63 24 (May) 392.00 394.23 394.33 1.000 99.41 99.76 392.94 25 (Jun) 393.00 395.12 394.92 0.999 99.51 99.52 394.91 26 (Jul) 391.00 396.01 395.42 0.999 98.88 98.87 395.46 27 (Aug) 392.00 396.89 396.12 0.998 98.96 99.25 394.96 28 (Sep) 396.00 397.78 397.25 0.999 99.69 99.74 397.02 29 (Oct) 395.00 398.67 398.12 0.999 99.22 99.78 395.86 30 (Nov) 400.00 399.56 398.75 0.998 100.31 100.48 398.11 31 (Dec) 409.00 400.45 102.33 399.69 32 (Jan) 404.00 401.34 100.95 400.21 33 (Feb) 404.00 402.23 99.84 404.67 34 (Mar) 405.00 403.12 99.39 407.47 35 (Apr) 399.00 404.01 100.09 398.63 36 (May) 402.00 404.90 99.76 402.97

------FORECAST------37 (Jun) (Zhat = 405.79)(S = 99.52)/100 = 403.82

39 (Using the template: “Trend+Season Forecasting.xls”) Forecasting with Trend and Seasonality Data t Year Month Y sn Deseasonalized 1 2001 6 Jun 375 99.51539 376.826 2 2001 7 Jul 370 98.87112 374.225 3 2001 8 Aug 374 99.25034 376.825 4 2001 9 Sep 378 99.7436 378.972 5 2001 10 Oct 376 99.78185 376.822 6 2001 11 Nov 380 100.4756 378.201 7 2001 12 Dec 384 102.3298 375.257 8 2002 1 Jan 380 100.9482 376.431 9 2002 2 Feb 378 99.8351 378.624 10 2002 3 Mar 380 99.39496 382.313 11 2002 4 Apr 382 100.0938 381.642 12 2002 5 May 383 99.76035 383.92 13 2002 6 Jun 382 99.51539 383.86 14 2002 7 Jul 381 98.87112 385.35 15 2002 8 Aug 385 99.25034 387.908 16 2002 9 Sep 387 99.7436 387.995 17 2002 10 Oct 390 99.78185 390.853 18 2002 11 Nov 392 100.4756 390.145 19 2002 12 Dec 403 102.3298 393.825 20 2003 1 Jan 398 100.9482 394.262 21 2003 2 Feb 393 99.8351 393.649 22 2003 3 Mar 389 99.39496 391.368 23 2003 4 Apr 394 100.0938 393.631 24 2003 5 May 392 99.76035 392.942 25 2003 6 Jun 393 99.51539 394.914 26 2003 7 Jul 391 98.87112 395.464 27 2003 8 Aug 392 99.25034 394.961 28 2003 9 Sep 396 99.7436 397.018 29 2003 10 Oct 395 99.78185 395.864 30 2003 11 Nov 400 100.4756 398.107 31 2003 12 Dec 409 102.3298 399.688 32 2004 1 Jan 404 100.9482 400.205 33 2004 2 Feb 404 99.8351 404.667 34 2004 3 Mar 405 99.39496 407.465 35 2004 4 Apr 399 100.0938 398.626 36 2004 5 May 402 99.76035 402.966

Forecast for June, 2004 = 403.886

40 Forecasts t Year Month Y 37 2004 6 Jun 403.886 38 2004 7 Jul 402.146 39 2004 8 Aug 404.567 40 2004 9 Sep 407.46 41 2004 10 Oct 408.499 42 2004 11 Nov 412.229 43 2004 12 Dec 420.742 44 2005 1 Jan 415.954 45 2005 2 Feb 412.252 46 2005 3 Mar 411.314 47 2005 4 Apr 415.092 48 2005 5 May 414.592

Seasonal Indices Month Index Jan 100.95 Feb 99.84 Mar 99.39 Apr 100.09 May 99.76 Jun 99.52 Jul 98.87 Aug 99.25 Sep 99.74 Oct 99.78 Nov 100.48 Dec 102.33

41 12-12. Using a computer: Linear regression trend line: Zhat(t) = 7.2043  0.0194 t

Centered C(t) = Ratio Seasonal [Desea- data: trend: Moving CMA Moving Index soned] t (mon.) Z(t) Zhat(t) Average Zhat(t) Average S Z(t)/S%

1 (Jul) 7.40 7.18 95.68 7.73 2 (Aug) 6.80 7.17 92.25 7.37 3 (Sep) 6.40 7.15 90.57 7.07 4 (Oct) 6.60 7.13 97.57 6.76 5 (Nov) 6.50 7.11 95.96 6.77 6 (Dec) 6.00 7.09 92.22 6.51 7 (Jan) 7.00 7.07 7.02 0.993 99.76 102.47 6.83 8 (Feb) 6.70 7.05 7.01 0.995 95.54 98.21 6.82 9 (Mar) 8.20 7.03 7.05 1.002 116.38 114.41 7.17 10 (Apr) 7.80 7.01 7.10 1.012 109.92 110.59 7.05 11 (May) 7.70 6.99 7.15 1.022 107.76 109.60 7.03 12 (Jun) 7.30 6.97 7.20 1.032 101.45 100.45 7.27 13 (Jul) 7.00 6.95 7.25 1.043 96.55 95.68 7.32 14 (Aug) 7.10 6.93 7.30 1.052 97.32 92.25 7.70 15 (Sep) 6.90 6.91 7.30 1.057 94.47 90.57 7.62 16 (Oct) 7.30 6.89 7.29 1.057 100.17 97.57 7.48 17 (Nov) 7.00 6.87 7.28 1.059 96.16 95.96 7.29 18 (Dec) 6.70 6.86 7.25 1.058 92.41 92.22 7.27 19 (Jan) 7.60 6.84 7.20 1.053 105.62 102.47 7.42 20 (Feb) 7.20 6.82 7.11 1.043 101.29 98.21 7.33 21 (Mar) 7.90 6.80 7.00 1.029 112.92 114.41 6.90 22 (Apr) 7.70 6.78 6.89 1.017 111.73 110.59 6.96 23 (May) 7.60 6.76 6.79 1.005 111.90 109.60 6.93 24 (Jun) 6.70 6.74 6.71 0.996 99.88 100.45 6.67 25 (Jul) 6.30 6.72 6.62 0.985 95.21 95.68 6.58 26 (Aug) 5.70 6.70 6.51 0.971 87.58 92.25 6.18 27 (Sep) 5.60 6.68 6.43 0.963 87.05 90.57 6.18 28 (Oct) 6.10 6.66 6.40 0.960 95.37 97.57 6.25 29 (Nov) 5.80 6.64 95.96 6.04 30 (Dec) 5.90 6.62 92.22 6.40 31 (Jan) 6.20 6.60 102.47 6.05 32 (Feb) 6.00 6.58 98.21 6.11 33 (Mar) 7.30 6.56 114.41 6.38 34 (Apr) 7.40 6.54 110.59 6.69

------FORECAST------35 (May) (Zhat = 6.525)(S = 109.60)/100 = 7.15 Template Forecast is 7.045

42 12-13. (Using the template: “Trend Forecast.xls”) Forecasting with Trend Data

Period t Zt mar 1 860 apr 2 860 may 3 875 jun 4 910 jul 5 890 aug 6 930 sep 7 970 oct 8 962 nov 9 957 dec 10 972 jan 11 975 feb 12 1000 mar 13 985 apr 14 1010

Forecast for May, 2004 = 1028.53 Forecast t Z-hat 15 1028.53 16 1040.37 17 1052.21 18 1064.05 19 1075.89 20 1087.74 21 1099.58 Regression Statistics 22 1111.42 2 23 1123.26 r 0.9122 24 1135.1 MSE 255.7634 25 1146.95 26 1158.79 Slope 11.84176 Intercept 850.9011

43 12.14.(Using the template: “Trend Forecast.xls”) Forecasting with Trend Data

Period t Zt apr 1 750 may 2 840 jun 3 895 jul 4 890 aug 5 900 sep 6 940 oct 7 955 nov 8 962 dec 9 1020 jan 10 1055 feb 11 1015 mar 12 1050

Forecast for May, 2004 = 1094.92 Forecast t Z-hat 13 1094.92 14 1118.86 15 1142.8 16 1166.74 17 1190.67 18 1214.61 19 1238.55 20 1262.48 Regression Statistics 21 1286.42 r2 0.9076 22 1310.36 MSE 834.21 23 1334.29 24 1358.23 Slope 23.93706 Intercept 783.7424

44 12.15.(Using the template: “Trend+Season Forecasting.xls”) Forecasting with Trend and Seasonality (quarterly) t Year Q Y Deseasonalized 1 2002 1 3.4 3.869621 2 2002 2 4.5 4.150717 3 2002 3 4 4.258289 4 2002 4 5 4.554288 5 2003 1 4.2 4.78012 6 2003 2 5.4 4.98086 7 2003 3 4.9 5.216404 8 2003 4 5.7 5.191888 9 2004 1 4.6 5.23537

Forecasts t Year Q Y 10 2004 2 6.20676 11 2004 3 5.56327 12 2004 4 6.71894

Seasonal Indices Q Index 1 87.86 2 108.42 3 93.93 4 109.79 400

Forecast for Q2, 2004 = 6.20676

45 12.16. Using a computer: w = 0.6 Zhat(1) = Z(1) = 142

Zhat( 2): 0.6(142.00) + 0.4(142.00) = 142.00 Zhat( 3): 0.6(137.00) + 0.4(142.00) = 139.00 Zhat( 4): 0.6(143.00) + 0.4(139.00) = 141.40 Zhat( 5): 0.6(142.00) + 0.4(141.40) = 141.76 Zhat( 6): 0.6(149.00) + 0.4(141.76) = 146.10 Zhat( 7): 0.6(143.00) + 0.4(146.10) = 144.24 Zhat( 8): 0.6(151.00) + 0.4(144.24) = 148.30 Zhat( 9): 0.6(150.00) + 0.4(148.30) = 149.32 Zhat(10): 0.6(151.00) + 0.4(149.32) = 150.33 Zhat(11): 0.6(146.00) + 0.4(150.33) = 147.73 Zhat(12): 0.6(144.00) + 0.4(147.73) = 145.49 Zhat(13): 0.6(145.00) + 0.4(145.49) = 145.20 ------FORECAST------Zhat(14): 0.6(147.00) + 0.4(145.20) = 146.28

By experimenting, we find that lower values of w in this case produce Zˆ values that agree more closely with the raw data at the end of the series.

(Using the template: “Exponential Smoothing.xls”) Exponential Smoothing

t Zt Forecast 1 142 142 2 137 142 3 143 139 4 142 141.4 5 149 141.76 6 143 146.104 7 151 144.242 8 150 148.297 9 151 149.319 10 146 150.327 11 144 147.731 12 145 145.492 13 147 145.197 14 146.279

Forecast for July, 2004 = 146.279

46 12.17. Using a computer: w = 0.3 Zhat(1) = Z(1) = 57 w = 0.8

Zhat( 2): 0.3(57.00) + 0.7(57.00) = 57.00 0.8(57.00) + 0.2(57.00) = 57.00 Zhat( 3): 0.3(58.00) + 0.7(57.00) = 57.30 0.8(58.00) + 0.2(57.00) = 57.80 Zhat( 4): 0.3(60.00) + 0.7(57.30) = 58.11 0.8(60.00) + 0.2(57.80) = 59.56 Zhat( 5): 0.3(54.00) + 0.7(58.11) = 56.88 0.8(54.00) + 0.2(59.56) = 55.11 Zhat( 6): 0.3(56.00) + 0.7(56.88) = 56.61 0.8(56.00) + 0.2(55.11) = 55.82 Zhat( 7): 0.3(53.00) + 0.7(56.61) = 55.53 0.8(63.00) + 0.2(55.82) = 53.56 Zhat( 8): 0.3(55.00) + 0.7(55.53) = 55.37 0.8(55.00) + 0.2(53.56) = 54.71 Zhat( 9): 0.3(59.00) + 0.7(55.37) = 56.46 0.8(59.00) + 0.2(54.71) = 58.14 Zhat(10): 0.3(62.00) + 0.7(56.46) = 58.12 0.8(62.00) + 0.2(58.14) = 61.23 Zhat(11): 0.3(57.00) + 0.7(58.12) = 57.79 0.8(57.00) + 0.2(61.23) = 57.85 Zhat(12): 0.3(50.00) + 0.7(57.79) = 55.45 0.8(50.00) + 0.2(57.85) = 51.57 Zhat(13): 0.3(48.00) + 0.7(55.45) = 53.21 0.8(48.00) + 0.2(51.57) = 48.71 Zhat(14): 0.3(52.00) + 0.7(53.21) = 52.85 0.8(52.00) + 0.2(48.71) = 51.34 Zhat(15): 0.3(55.00) + 0.7(52.85) = 53.50 0.8(55.00) + 0.2(51.34) = 54.27 Zhat(16): 0.3(58.00) + 0.7(53.50) = 54.85 0.8(58.00) + 0.2(54.27) = 57.25 Zhat(17): 0.3(61.00) + 0.7(54.85) = 56.69 0.8(61.00) + 0.2(57.25) = 60.25

The w = .8 forecasts follow the raw data much more closely. This makes sense because the raw data jump back and forth fairly abruptly, so we need a high w for the forecasts to respond to those oscillations sooner.

12.18. Using a computer: w = 0.7 Zhat(1) = Z(1) = 195

Zhat( 2): 0.7(195.00) + 0.3(195.00) = 195.00 Zhat( 3): 0.7(193.00) + 0.3(195.00) = 193.60 Zhat( 4): 0.7(190.00) + 0.3(193.60) = 191.08 Zhat( 5): 0.7(185.00) + 0.3(191.08) = 186.82 Zhat( 6): 0.7(180.00) + 0.3(186.82) = 182.05 Zhat( 7): 0.7(190.00) + 0.3(182.05) = 187.61 Zhat( 8): 0.7(185.00) + 0.3(187.61) = 185.78 Zhat( 9): 0.7(186.00) + 0.3(185.78) = 185.94 Zhat(10): 0.7(184.00) + 0.3(185.94) = 184.58 Zhat(11): 0.7(185.00) + 0.3(184.58) = 184.87 Zhat(12): 0.7(198.00) + 0.3(184.87) = 194.06 Zhat(13): 0.7(199.00) + 0.3(194.06) = 197.52 Zhat(14): 0.7(200.00) + 0.3(197.52) = 199.26 Zhat(15): 0.7(201.00) + 0.3(199.26) = 200.48 Zhat(16): 0.7(199.00) + 0.3(200.48) = 199.44 Zhat(17): 0.7(187.00) + 0.3(199.44) = 190.73 Zhat(18): 0.7(186.00) + 0.3(190.73) = 187.42 Zhat(19): 0.7(191.00) + 0.3(187.42) = 189.93 Zhat(20): 0.7(195.00) + 0.3(189.93) = 193.48 Zhat(21): 0.7(200.00) + 0.3(193.48) = 198.04

47 Zhat(22): 0.7(200.00) + 0.3(198.04) = 199.41 Zhat(23): 0.7(190.00) + 0.3(199.41) = 192.82 Zhat(24): 0.7(186.00) + 0.3(192.82) = 188.05 Zhat(25): 0.7(196.00) + 0.3(188.05) = 193.61 Zhat(26): 0.7(198.00) + 0.3(193.61) = 196.68 Zhat(27): 0.7(200.00) + 0.3(196.68) = 199.01 ------FORECAST------Zhat(28): 0.7(200.00) + ).3(199.01) = 199.70

Exponential Smoothing

MAE MAPE MSE w 0.7 4.8241 2.52% 34.8155

2 t Zt Forecast |Error| %Error Error 1 195 195 2 193 195 3 190 193.6 3.6 1.89% 12.96 4 185 191.08 6.08 3.29% 36.9664 5 180 186.824 6.824 3.79% 46.567 6 190 182.047 7.9528 4.19% 63.247 7 185 187.614 2.61416 1.41% 6.83383 8 186 185.784 0.21575 0.12% 0.04655 9 184 185.935 1.93527 1.05% 3.74529 10 185 184.581 0.41942 0.23% 0.17591 11 198 184.874 13.1258 6.63% 172.287 12 199 194.062 4.93775 2.48% 24.3814 13 200 197.519 2.48132 1.24% 6.15697 14 201 199.256 1.7444 0.87% 3.04292 15 199 200.477 1.47668 0.74% 2.18059 16 187 199.443 12.443 6.65% 154.828 17 186 190.733 4.7329 2.54% 22.4004 18 191 187.42 3.58013 1.87% 12.8173 19 195 189.926 5.07404 2.60% 25.7459 20 200 193.478 6.52221 3.26% 42.5392 21 200 198.043 1.95666 0.98% 3.82853 22 190 199.413 9.413 4.95% 88.6046 23 186 192.824 6.8239 3.67% 46.5656 24 196 188.047 7.95283 4.06% 63.2475 25 198 193.614 4.38585 2.22% 19.2357 26 200 196.684 3.31575 1.66% 10.9942 27 200 199.005 0.99473 0.50% 0.98948 28 199.702

48 12.19. Using a computer: w = 0.6 Zhat(1) = Z(1) = 16.4

Zhat( 2): 0.6(16.40) + 0.4(16.40) = 16.40 Zhat( 3): 0.6(17.10) + 0.4(16.40) = 16.82 Zhat( 4): 0.6(16.90) + 0.4(16.82) = 16.87 Zhat( 5): 0.6(17.30) + 0.4(16.87) = 17.13 Zhat( 6): 0.6(17.50) + 0.4(17.13) = 17.35 Zhat( 7): 0.6(17.20) + 0.4(17.35) = 17.26 Zhat( 8): 0.6(17.30) + 0.4(17.26) = 17.28 Zhat( 9): 0.6(17.10) + 0.4(17.28) = 17.17 Zhat(10): 0.6(16.90) + 0.4(17.17) = 17.01 Zhat(11): 0.6(17.00) + 0.4(17.01) = 17.00 Zhat(12): 0.6(17.10) + 0.4(17.00) = 17.06 ------FORECAST------Zhat(13): 0.6(17.20) + 0.4(17.06) = 17.14

(Using the template: “Exponential Smoothing.xls”) Exponential Smoothing

t Zt Forecast 1 16.4 16.4 2 17.1 16.4 3 16.9 16.82 4 17.3 16.868 5 17.5 17.1272 6 17.2 17.3509 7 17.3 17.2604 8 17.1 17.2841 9 16.9 17.1737 10 17 17.0095 11 17.1 17.0038 12 17.2 17.0615 13 17.1446

Forecast for May, 2004 = 17.1446

12.20. Answers will vary.

12.21. Equation (12-11): ˆ 2 3 Z t1  wZ t  w(1 w)Z t1  w(1  w) Z t2  w(1 w) Z t3  ... ˆ The same equation for Z t (shifting all subscripts back by 1): ˆ 2 3 Z t = wZ t1 + w(1w)Z t2 + w(1-w) Z t3 + w(1-w) Z t4 + …

49 Now multiplying this second equation throughout by (1w) gives: ˆ 2 3 4 (1w) Z t = w(1w)Z t-1 + w(1w) Z t-2 + w(1w) Z t3 = w(1w) Z t-4 + …

Now note that all the terms on the right side of the equation above are identical to all the terms in

Equation (12-11) on the top, after the term wZ t. Hence we can substitute in Equation (12-11) the ˆ left hand side of our last equation, (1w) Z t for all the terms past the first. This gives us: ˆ ˆ Z t1  wZ t  (1  w)Z t which is Equation (12-12).

ˆ ˆ 12-22. Equation (12-13) is: Zt+1 = Zt + (1 w)(Zt Zt ) Multiplying out we get: ˆ ˆ ˆ ˆ Z t1  Z t  (1  w)Z t  (1  w)Z t  Z t  (1  w)Z t  Z t  wZ t  wZ t  (1  w)Z t , which is Equation (12-12).

289.1 12-23. Simply divide each CPI by ; thus: 100 year old CPI new CPI 1950 72.1 24.9 1951 77.8 26.9 1952 79.5 27.5 1953. 80.1. 27.7. . . .

12-24. 168.77 in July 2000 and 173.48 in June 2001.

12-25. A simple price index reflects changes in a single price variable of time, relative to a single base time.

12-26. Index numbers are used as deflators for comparing values and prices over time in a way that prevents a given inflationary factor from affecting comparisons. They are also used to provide an aggregate measure of changes over time in several related variables.

50 12-27. a. 1988 1993 index 163 b. Just divide each index number by = 1988 index 100 c. It fell, from 145% of the 1988 output down to 133% of that output. d. Big increase in the mid ‘80’s, then a sharp drop in 1986, tumbling for three more years, then slowly climbing back up until 1995, then a drop-off.

a) Price Index

BaseYear 1988 100 Base Year Price Index 1984 175 175 1985 190 190 1986 132 132 1987 96 96 1988 100 100 1989 78 78 1990 131 131 1991 135 135 1992 154 154 1993 163 163 1994 178 178 1995 170 170 1996 145 145 1997 133 133

c) Price Index

BaseYear 1993 163 Base Year Price Index 1984 175 107.36 1985 190 116.56 1986 132 80.982 1987 96 58.896 1988 100 61.35 1989 78 47.853 1990 131 80.368 1991 135 82.822 1992 154 94.479 1993 163 100 1994 178 109.2 1995 170 104.29 1996 145 88.957 1997 133 81.595

51 Jan.2004value 12-28. Divide each data point by  1.44 : 100 Jun. ’03: 98.6 Jul. ’03: 95.14 …

12-29. Since a yearly cycle has 12 months and there are only 18 data points, a seasonal/cyclical decomposition isn’t feasible. Simple linear regression, with the successive months numbered 1,2,..., gives SALES = 4.23987  .03870MONTH, thus for July 1995 (month #19), the forecast is 3.5046. (Using the template: “Trend Forecast.xls”) Forecasting with Trend Data

Period t Zt jan 1 4.4 feb 2 4.2 mar 3 3.8 apr 4 4.1 may 5 4.1 jun 6 4 jul 7 4 aug 8 3.9 sep 9 3.9 oct 10 3.8 nov 11 3.7 dec 12 3.7 jan 13 3.8 feb 14 3.9 mar 15 3.8 apr 16 3.7 may 17 3.5 jun 18 3.4

Forecast t Z-hat 19 3.50458 20 3.46588 21 3.42718 The forecast of sales for July, 2004 is 3.5 million units.

Regression Statistics r2 0.7285 MSE 0.016906

Slope -0.0387 Intercept 4.239869

12-30. Trend analysis is a quick, if sometimes inaccurate, method that can give good results. The additive and multiplicative TSCI models are sometimes useful, although they lack a firm theoretical framework. Exponential smoothing methods are good models. The ones described in

52 this book do not handle seasonality, but extensions are possible. This author believes that Box- Jenkins ARIMA models are the way to go. One limitation of these models is the need for large data sets.

12-31. Exponential smoothing models smooth the data of sharp variations and produce forecasts that follow a type of “average” movement in the data. The greater the weighting factor w, the closer the exponential smoothing series follows the data and forecasts tend to follow the variations in the data more closely.

12-32. The trend regression is: (Using the template: “Trend Forecast.xls”) Forecasting with Trend Data

Period t Zt 1999 1 340 2000 2 370 2001 3 350 2002 4 660 2003 5 1620

Forecast t Z-hat 6 1523 7 1808

Forecast for 2004 = 1523 Regression Statistics r2 0.6747 MSE 130543.3

Slope 285 Intercept -187

53 12-33. An exponential regression from Minitab gives: t Yt = 4.47535(1.14077) y(1998) = 62.343

12-34. a) raised the seasonal index to 99.38 for April from 99.29 We would expect to see the April index change by a significant amount. The reason it did not is due to the calculations involving moving average. b) raised the seasonal index to 122.27 for April from 99.29 c) raised the seasonal index to 100.16 for December from 100.09 We would expect the December index to change by a significant amount. It did not due to the calculations for moving average. d) very high or low values for data points at the beginning or end of a series have little impact on the seasonal index due to their limited influence in the moving average computations.

12-35. (Using the template: “Trend Forecast.xls”)

Forecasting with Trend Data

Period t Zt 1998 1 6.3 1999 2 6.6 2000 3 7.3 2001 4 7.4 2002 5 7.8 2003 6 6.9 2004 7 7.8

Forecast t Z-hat 8 7.95714 9 8.15714 10 8.35714 Forecast for 2005 = 7.957

Regression Statistics r2 0.5552 MSE 0.179429

Slope 0.2 Intercept 6.357143

12-36. Answers will vary.