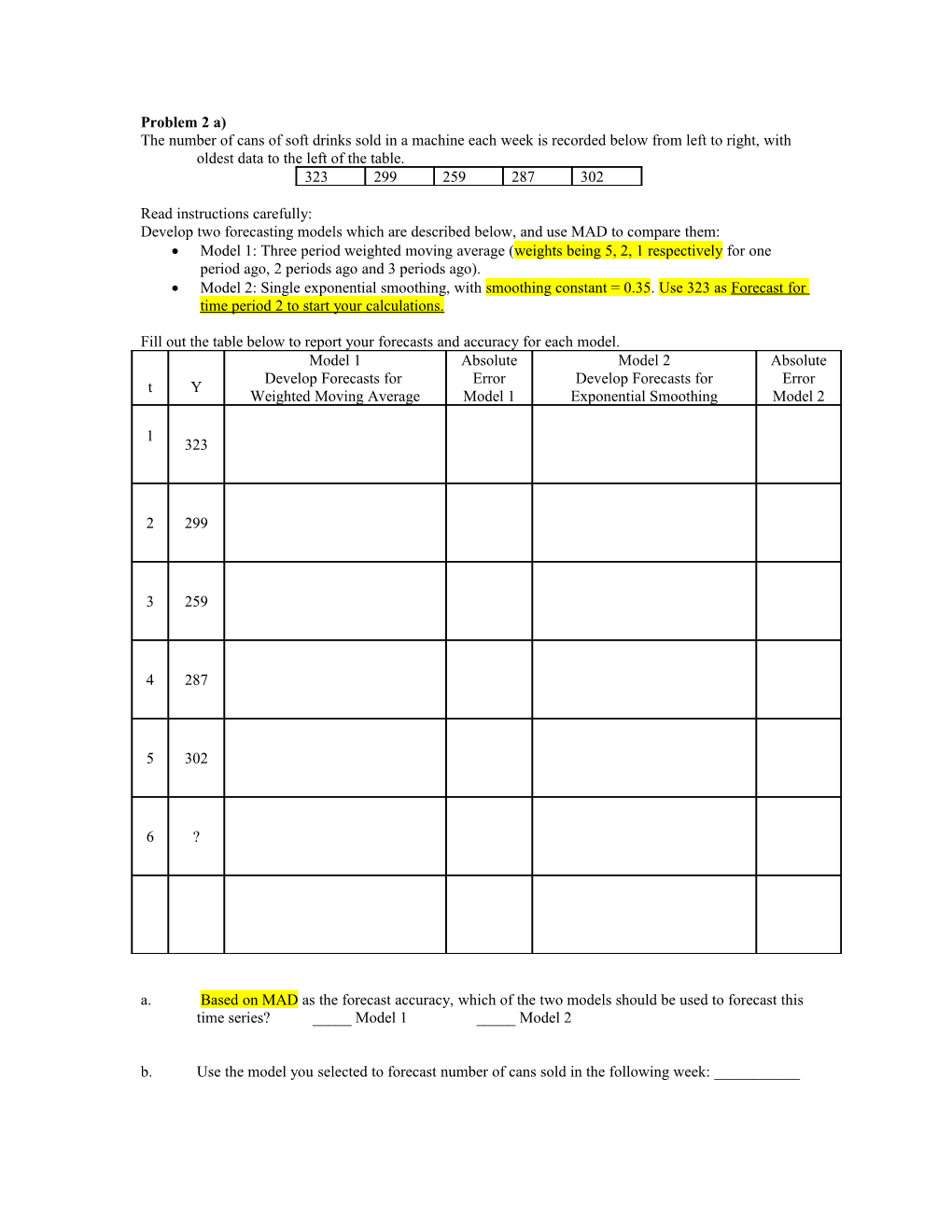
The Number of Cans of Soft Drinks Sold in a Machine Each Week Is Recorded Below from Left

Problem 2 a) The number of cans of soft drinks sold in a machine each week is recorded below from left to right, with oldest data to the left of the table. 323 299 259 287 302

Read instructions carefully: Develop two forecasting models which are described below, and use MAD to compare them:  Model 1: Three period weighted moving average (weights being 5, 2, 1 respectively for one period ago, 2 periods ago and 3 periods ago).  Model 2: Single exponential smoothing, with smoothing constant = 0.35. Use 323 as Forecast for time period 2 to start your calculations.

Fill out the table below to report your forecasts and accuracy for each model. Model 1 Absolute Model 2 Absolute Develop Forecasts for Error Develop Forecasts for Error t Y Weighted Moving Average Model 1 Exponential Smoothing Model 2

1 323

2 299

3 259

4 287

5 302

6 ?

a. Based on MAD as the forecast accuracy, which of the two models should be used to forecast this time series? _____ Model 1 _____ Model 2 b. Use the model you selected to forecast number of cans sold in the following week: ______Problem 2 b) In the space provided, draw the network for this project. Use the 3 time estimates provided for each activity (in weeks) to estimate the expected time and variance for the activities. Then work the network forward and backward to arrive at the expected project completion time. a. What are the critical activities? ______b. What is the expected time for this project? ______weeks c. What is the standard deviation of time for this project? ______weeks d. What is the probability that the project will take longer than 30 weeks? ______e. What should be the promised due date if it is desired to meet that due date with a 97% probability? Answer: ______weeks from start of the project should be set as the promised due date.

Show network and calculations below. Fill out the columns in the table.

e t a i e d t h h t e r s c y s c m i r i l a i i e i ? m t t a t n y e t l c n i t

s t s i S k i f a k i i n m

d i c c t F I v l t a e i

i t m s i m a r s t t t i t t i s l e r i e o s c s t s c i e i S r a s l s e e l t o p t s A r e r p a C V e a a O a P M x c L L E e E E d e r p A - 2 4 6

B - 5 9 13

C A 4 7 10

D A 6 9 12

E C, D 1 3 5

F C, E 10 11 12

G B,E 3 6 9

Problem 2 c) Test problem -- Crash schedule solution Normal Crash Normal Crash Crash Crash by Crashing cost time time Cost Cost cost/pd Project 22. 16. A 12. 8. 8,000. 12,000. 1,000. 4. 4,000. B 14. 10. 5,000. 7,500. 625. 3. 1,875. C 8. 8. 10,000. 10,000. 0. 0. 0. D 5. 3. 6,000. 8,000. 1,000. 0. 0. E 4. 3. 5,000. 7,000. 2,000. 1. 2,000. F 6. 5. 9,000. 12,000. 3,000. 1. 3,000. G 10. 8. 5,000. 8,000. 1,500. 2. 3,000. TOTALS 48,000. 13,875.

Test problem -- Crash schedule solution Project time Period cost Cumulative cost A B C D E F G 22 0. 0. 21 1,000. 1,000. 1. 20 1,000. 2,000. 2. 19 1,625. 3,625. 3. 1. 18 1,625. 5,250. 4. 2. 17 4,125. 9,375. 4. 3. 1. 1. 16 4,500. 13,875. 4. 3. 1. 1. 2.

Use the printout from DS for Windows that appear above to answer the following. Assume time units are in weeks. a. What is the normal duration for this project? ______weeks b. What is the normal cost for this project? $______c. Which activity (ies) can be crashed? List them: ______d. Which activity (ies) should be crashed to finish the project in 17 weeks? ______e. Which activity (ies) can be crashed, but we will never crash it (them)? ______f. What is the minimum number of weeks in which this project can be done (assuming we have enough resources to allocate to it)? ______weeks g. Assume you have already crashed the project down to 20 weeks. But you need to reduce it further down to 19 weeks. For that one period of reducing the project time from 20 to 19 weeks, which activity (ies) must be crashed, for how many weeks, and at what cost? Activity Wks to crash Cost to crash

h. If you want to finish this project in 17 weeks, what would be the total cost of this project at the time of completion? $______

Problem 2 d) The life expectancy of Timely brand watches is normally distributed with a mean of four years and a standard deviation of 8 months. Please answer the following questions. Hint: Convert 4 years to months and perform/report all calculations in terms of months!

For all parts, show your work, and put your final answer on the lines provided. a. What is the probability that a randomly selected watch will be in working condition for “more than” five years (60 months)? ______b. The company has a three-year warranty period on their watches (36 months). What percentage of their watches will be in operating condition “after” the warranty period? ______%

c. What is the minimum and the maximum life expectancy of the “middle 95%” of the watches? Min: ______months, Max: ______months

d. Ninety-five percent of the watches will have a life expectancy of “at least” how many months? ______months Problem 2 e) The average length of a T.V. commercial is 1.2 minutes (72 seconds). Assume the exponential distribution is applicable. a. What is the probability that a TV commercial takes less than one minute? ______

b. What is the probability that a commercial takes between 45 seconds to 1 minute?

Problem 2 f) A quality control manager is investigating the number of defective computer chips found in batches produced during the past week of production. From the past week quality control records, the number of defective follows the distribution below: X= no. of defectives f(X) Show your work for part c. 0 0.15

1 0.2

2 0.3

3 0.2

4 0.1

5 0.05

a. What is the probability that a batch has at least 3 defective chips? ______

b. What is the probability that a batch has no more than 1 defective? ______

c. On the average, how many defective units are in a batch? ______