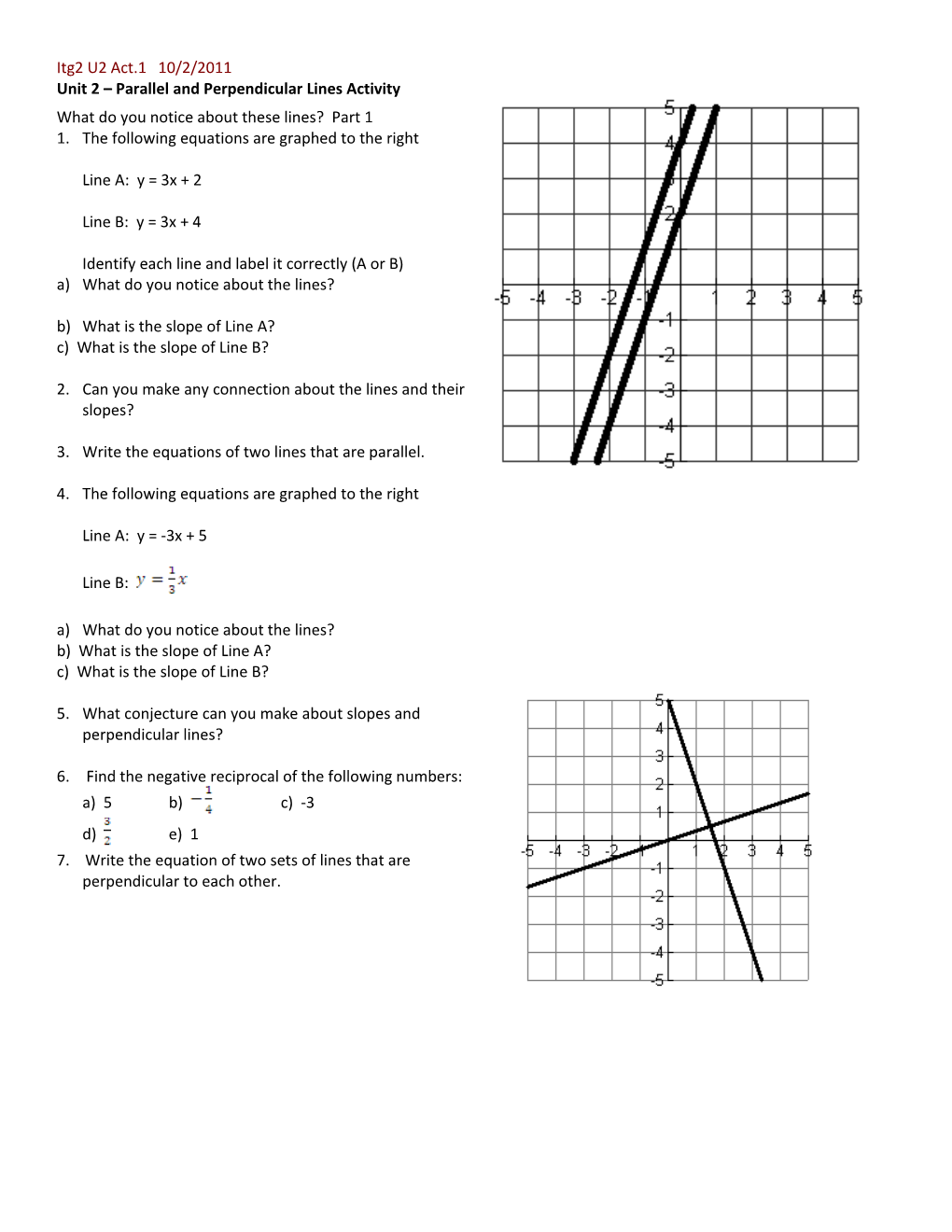
Itg2 U2 Act.1 10/2/2011 Unit 2 – Parallel and Perpendicular Lines Activity What do you notice about these lines? Part 1 1. The following equations are graphed to the right
Line A: y = 3x + 2
Line B: y = 3x + 4
Identify each line and label it correctly (A or B) a) What do you notice about the lines? b) What is the slope of Line A? c) What is the slope of Line B?
2. Can you make any connection about the lines and their slopes?
3. Write the equations of two lines that are parallel.
4. The following equations are graphed to the right
Line A: y = -3x + 5
Line B: a) What do you notice about the lines? b) What is the slope of Line A? c) What is the slope of Line B?
5. What conjecture can you make about slopes and perpendicular lines?
6. Find the negative reciprocal of the following numbers: a) 5 b) c) -3 d) e) 1 7. Write the equation of two sets of lines that are perpendicular to each other. Itg2 U2 WS2.1 Itg2 U2 WS2.2 Unit 2 – Parallel and Perpendicular Lines Unit 2 – Slope-Intercept form (Solve for Y) 1. a) Define parallel. b) Define perpendicular. 1. Which of the three forms of equations do you like a) Parallel lines are lines that never intersect and best? Why? always are the same distance from each other. 2 To find the slope which form would you prefer? b) Perpendicular lines are lines that intersect each I like a line equation that has the slope in it. Thus I other at a right angle. prefer Slope-intercept or Modified Point Slope. 2 What do you know about the slopes of parallel lines? Rewrite each equation below in slope-intercept form (in other Slopes of parallel lines are the same. words, solve for y). Then write the equation of ANY line that is parallel to the given line. And then write the equation of ANY 3. What do you know about the slopes of perpendicular line which is perpendicular. You may write your equations in lines? slope-intercept form. Slopes of perpendicular lines are the opposite 3. 4x + y = 11 reciprocals of each other. - 4x -4x Opposite means the sign changes, so if one slope sign y = - 4x + 11 is positive the other will be negative or vice versa. The term reciprocal means the numerator and 4. x – y = 3 - x - x denominator switch so the number that was on top is - y = - x + 3 now on bottom and vice versa. y = x – 3 For each set of equations below, tell whether the two lines 5. 5x – 10y = 9 are parallel to each other, perpendicular to each other or - 5x - 5x neither. -10y = - 5x + 9 -10 -10 4. y = 2x – 5 and y = 2x + 8 5 9 y = /10 – /10 m1 = 2 m2 = 2 1 9 y = /2 – /10 Therefore the slopes are ||slopes to each other 6. -3x + 2y = 8 1 5. y = /4 x + 3 and y = - 4x – 3 +3x +3x 1 m1 = /4 m2 = - 4 2y = 3x + 8 Therefore slopes are to each other 2 2 1 3 6. y = - 2x + 8 and y = - /2 x - 10 y = /2 x + 4 1 m1 = -2 m2 = - /2 7. -6x – 3y = 9 Therefore the slopes are neither ||nor +6x +6x 7. y = 12x – 1 and y = 12x + 3 -3y = 6x + 9 -3 -3 m1 = 12 m2 = 12
Therefore the slopes are ||slopes to each other y = -2x – 3 1 1 8. 9x + 2y = 16 8. y = /2 (x – 8) + 3 and y = - /2 (x + 4) – 1 1 1 -9x -9x m1 = /2 m2 = - /2 2y = -9x + 16 Therefore the slopes are neither ||nor 2 2 2 3 9 9. y = /3 (x + 6) – 2 and y = /2 (x – 2) + 9 y = - /2 x + 8 m = 2/ m = 3/ 1 3 2 2 9. -7x – 2y = 10 Therefore the slopes are neither || nor + 7x +7x 2 3 10. y = /3 x – 7 and y = - /2 x + 9 -2y = 7x + 10 2 3 m1 = /3 m2 = - /2 -2 -2 7 Therefore slopes are to each other y = /2 x – 5
1 11. y = - 4x and y = /4 x – 4 10. x + 5y = 15 1 m1 = - 4 m2 = /4 -x -x Therefore slopes are to each other 5y = -x + 15 5 5 1 y = - /5 x + 3 Itg2 U2 WS2.3 5. A line that passes through the point (-6, 1) and is parallel 1 Integrated Math 2 – Parallel Lines WS #2-3 to the line y = /2 x – 2 1 For each problem below write the equation of the line m = /2 , (-6, 1) 1 in all three forms and graph BOTH lines to make sure y = /2 (x + 6) + 1 1 you are correct. y = /2 x + 3 + 1 y = 1/ x + 4 1. How can you tell if two lines are parallel before 2 2y = x + 8 graphing them? -x + 2y = 16 Two lines are parallel if they have the same slope and x – 2y = -16 have different y-intercepts. 1 Graph a) y = /2 x – 2 (Original equation) 1 For each problem below, write the equation of the Graph b) y = /2 x + 4 (New equation) line in all three forms and graph BOTH lines to make Check to be sure equations lines on graph are parallel sure you are correct. as confirmation. 2. A line that passes through the point (-2, 5) and is parallel to the line y = x + 2 6. A line that passes through the point (-27, -12) and is 2 A parallel slope means that the slope is the same. parallel to the line y = /3 x – 2 2 m = 1, (-2, 5) m = /3, (-27, -12) 2 y = 1(x + 2) + 5 y = /3 (x + 27) – 12 2 y = x + 2 + 5 y = /3 x + 18 – 12 2 y = x + 7 y = /3 x + 6 -x + y = 7 3y = 2x + 18 x – y = - 7 -2x + 3y = 18 Graph a) y = x + 2 (Original equation) 2x – 3y = -18 2 Graph b) y = x + 7 (New equation) Graph a) y = /3 x – 2 (Original equation) 2 Check to be sure equations lines on graph are parallel Graph b) y = /3 x + 6 (New equation) as confirmation. Check to be sure equations lines on graph are parallel as confirmation. 3. A line that passes through the point (1, 4) and is parallel to the line y = -3x + 1 7. A line that passes through the point (10, 3) and is m = -3, (1, 4) 3 parallel to the line y = /5 x – 1 y = -3(x – 1) + 4 3 m = /5, (10, 3) y = -3x + 3 + 4 3 y = /5 (x – 10) + 3 y = -3x + 7 3 y = /5 x – 6 + 3 3 3x + y = 7 y = /5 x – 3 5y = 3x – 15 Graph a) y = -3x + 1 (Original equation) -3x + 5y = -15 Graph b) y = -3x + 7 (New equation) 3x – 5y = 15 Check to be sure equations lines on graph are parallel 3 Graph a) y = /5 x – 1 (Original equation) as confirmation. 3 Graph b) y = /5 x – 3 (New equation) 4. A line that passes through the point (0, 2) and is Check to be sure equations lines on graph are parallel parallel to the line y = 5x – 6 as confirmation. m = 5, (0, 2) y = 5(x – 0) + 2 ------y = 5x – 0 + 2 y = 5x + 2 -5x + y = 2 5x – y = 2 Graph a) y = 5x – 6 (Original equation) Graph b) y = 5x + 2 (New equation) Check to be sure equations lines on graph are parallel as confirmation. Itg2 U2 WS2.4 Integrated Math 2 – Perpendicular Lines WS #2-4 1. a) What does opposite reciprocal mean? b) What types of slopes does it refer to? Slopes that are opposite reciprocals are slopes. Opposite means the sign changes, so if one slope sign is positive the other will be negative or vice versa. The term reciprocal means the numerator and denominator switch so the number that was on top is now on bottom and vice versa. For each problem below, write the equation of the line in all three forms (You may wish to Graph BOTH lines to make sure you are doing them are correct). 2. A line that passes through the point (-1, 4) and is perpendicular to the line y = x + 2 m = - 1, (-1, 4) y = -1(x + 1) + 4 y = -1x – 1 + 4 y = -1x + 3 + x + x x + y = 3 Graph a) y = x + 2 (Original equation) Graph b) y = -x + 3 (New equation) Check to be sure equations lines on graph are perpendicular as confirmation. 3. A line that passes through the point (6, 2) and is perpendicular to the line y = -3x + 1 1 m = /3, (-1, 4) 1 y = /3 (x – 6) + 2 1 y = /3 x – 2 + 2 1 y = /3 x 3y = x + 0 – x – x -x + 3y = 0 x – 3y = 0 Graph a) y = - 3x + 1 (Original equation) 1 Graph b) y = /3 (New equation) Check to be sure equations lines on graph are perpendicular as confirmation. 4. A line that passes through the point (0, 2) and is perpendicular to y = 5x – 6 1 m = - /5, (0, 2) 1 y = - /5 (x – 0) + 2 1 y = - /5 x + 2 5y = - x + 10 + x + x x + 5y = 10 Graph a) y = 5x – 6 (Original equation) 1 Graph b) y = - /5 x + 2 (New equation) Check to be sure equations lines on graph are perpendicular as confirmation. 1 5. A line that is perpendicular to y = /2 (x – 2) – 4, and passes through the point (-1, -1) m = -2, (-1, -1) y = -2(x + 1) – 1 y = -2x – 2 – 1 y = - 2x – 3 + 2x + 2x 2x + y = 3 1 Graph a) y = /2 x – 3 (Original equation) Graph b) y = - 2x – 3 (New equation) Check to be sure equations lines on graph are perpendicular as confirmation.
6. A line that is perpendicular to -2x + 3y = 9, and passes through the point (-12, 7) -2x + 3y = 9 3y = 2x + 9 2 y = /3 x + 3 3 m = - /2, (-12, 7) 3 y = - /2 (x + 12) + 7 3 y = - /2 x – 18 + 7 3 y = - /2 x – 11 2y = -3x – 22 + 3x + 3x 3x + 2y = -22 2 Graph a) y = /3 x + 3 (Original equation) 3 Graph b) y = - /2 x – 11 (New equation) Check to be sure equations lines on graph are perpendicular as confirmation.
7. A line that is perpendicular to 4x + y = – 1, and passes through the point (-8, -3) 4x + y = -1 y = - 4x – 1 1 m = /4, (- 8, - 3) 1 y = /4 (x + 8) – 3 1 y = /4 x + 2 – 3 1 y = /4 x – 1 4y = x – 4 – x – x -x + 4y = - 4 x – 4y = 4 Graph a) y = - 4x – 1 (Original equation) 1 Graph b) y = /4 x – 1 (New equation) Check to be sure equations lines on graph are perpendicular as confirmation. 8 Itg2 U2 PQz1 - Prep1 for Quiz Fall 2011 slope: y = - /7 x + # Integrated Math 2 – Unit 2 Practice Quiz – || and For each problem below, write the equation of the line For questions 1-4 below, determine if the lines are parallel ( || ), in all three forms. GRAPH BOTH LINES to check your perpendicular ( ), or neither and explain why. (3 points each) answers. (7 points each) 1. y = 3x – 5 and y = -5(x + 1) – 2 8. A line that passes through the point (2, 8) and is parallel to the line y = 3x – 6 m1 = 3 m2 = -5 m = 3, (2, 8) Therefore slopes are neither || nor y = 3(x – 2) + 8 5 2. -3x + 5y = 15 and y = - /3 x + 6 y = 3x – 6 + 8 5y = 3x + 15 y = 3x + 2 3 y = /5 – 3 -3x + y = 2 3 5 m1 = /5 m2 = - /3 3x – y = - 2 Therefore slopes are to each other Graph a) y = 3x – 6 (Original equation) 2 2 Graph b) y = 3x + 2 (New equation) 3. y = /3 (x – 6) + 4 and y = /3 x – 5 2 2 Check to be sure equations lines on graph are parallel m1 = /3 m2 = /3 as confirmation. Therefore slopes are ||slopes to each other 9. A line that passes through the point (-9, -5) and is 4. -4x + y = 7 and y = 1/ x – 4 4 perpendicular to the line y = -3x – 7 y = 4x + 7 1 1 m = /3 , (-9, -5) m1 = 4 m2 = /4 1 y = /3 (x + 9) – 5 Slopes are neither || nor (Although the slopes are 1 y = /3 x + 3 – 5 reciprocals of each other they are not the opposite 1 y = /3 x – 2 signs. (The sign did not change) 3y = x – 6 5. a) What does opposite reciprocal mean? (2 points) -x + 3y = -6 b) What types of slopes does it refer to? x + 3y = 6 Slopes that are opposite reciprocals are slopes. Graph a) y = -3x – 7 (Original equation) 1 Opposite means the sign changes, so if one slope sign Graph b) y = /3 x – 2 (New equation) is positive the other will be negative or vice versa. Check to be sure equations lines on graph are The term reciprocal means the numerator and perpendicular as confirmation. 1 denominator switch so the number that was on top is 10. A line that is parallel to the line y = - /4 x + 1, and now on bottom and vice versa. passes through the point (2, 2) m = - 1/ , (12, 2) Rewrite each equation below in slope-intercept 4 y = - 1/ (x – 12) + 2 form. Then write the equation of any line that is 4 y = - 1/ x + 3 + 2 parallel to the given line AND perpendicular to the 4 y = - 1/ x + 5 given line. (4 points each) 4 4y = x + 20
-x + 4y = 20 6. 3x + 4y = 20 x – 4y = -20 -3x -3x 1 Graph a) y = - /4 x + 1 (Original equation) 4y = - 3x + 20 1 Graph b) y = - /4 x + 5 (New equation) 4 4 Check to be sure equations lines on graph are parallel 3 y = - /4 x + 5 as confirmation. 3 m1 = - /4 11. A line that is perpendicular to the line y = 1/ x – 2, || slope: y = - 3/ x + # 3 4 and passes through the point (-4, 8) slope: y = 4 /3 x + # m = - 3, (-4, 8) 7. 7x – 8y = -80 y = - 3(x + 4) + 8 -7x -7x y = -2x – 12 + 8 - 8y = - 7x – 80 y = -2x – 4 -8 -8 2x + y = - 4 7 1 y = /8 – 10 Graph a) y = /3 x – 2 (Original equation) 7 m1 = /8 Graph b) y = -2x – 4 (New equation) 7 || slope: y = /8 x + # Check to be sure equations lines on graph are perpendicular as confirmation. 4 Itg2 U2 PQz1.2 - Prep2 for Quiz Fall 2011 slope: y = - /7 x + # Integrated Math 2 – Unit 2 Practice Quiz – || and For each problem below, write the equation of the line For questions 1-4 below, determine if the lines are parallel ( || ), in all three forms. GRAPH BOTH LINES to check your perpendicular ( ), or neither and explain why. (3 points each) answers. (7 points each) 2 2 1. y = /3 (x – 6) + 3 and y = /3 x – 4 8. A line that passes through the point (8, -2) and is 2 2 3 m1 = /3 m2 = /3 parallel to the line y = - /4 x – 5 3 Therefore slopes are ||slopes to each other m = - /4, (8, -2) 3 4 y = - /4 (x – 8) – 2 2. y = /3 x – 2 and - 3x + 4y = 20 3 y = - /4 x + 6 – 2 4y = 3x + 20 3 3 y = - /4 x + 4 y = /4 x + 5 4 3 4y = -3x + 16 m1 = /3 m2 = /4 3x + 4y = 16 Slopes are neither || nor (Although the slopes are Graph a) y = - 3/ x – 5 (Original equation) reciprocals of each other they are not the opposite 4 Graph b) y = - 3/ x + 4 (New equation) signs. (The sign did not change) 4 Check to be sure equations lines on graph are parallel 3. y = - 4(x – 2) – 5 and y = 3x – 7 as confirmation. m = -4 m = 3 1 2 9. A line that passes through the point (6, 4) and is Therefore slopes are neither || nor perpendicular to the line y = -3x + 1 3 4. y = - /2 x + 6 and - 2x + 3y = - 15 1 m = /3 , (6, 4) 3y = 2x – 15 1 2 y = /3 (x – 6) + 4 y = /3 x – 5 1 3 2 y = /3 x – 2 + 4 m1 = - /2 m2 = /3 1 y = /3 x + 2 Therefore slopes are to each other 3y = x + 6 -x + 3y = 6 5. a) What does opposite reciprocal mean? (2 points) x – 3y = - 6 b) What types of slopes does it refer to? Graph a) y = - 3x + 1 (Original equation) Slopes that are opposite reciprocals are slopes. 1 Graph b) y = /3 x + 2 (New equation) Opposite means the sign changes, so if one slope sign Check to be sure equations lines on graph are is positive the other will be negative or vice versa. perpendicular as confirmation. The term reciprocal means the numerator and 10. A line that is parallel to the line y = 2x + 4, and denominator switch so the number that was on top is passes through the point (3, 5) now on bottom and vice versa. m = 2 , (3, 5) Rewrite each equation below in slope-intercept y = 2(x – 3) + 5 form. Then write the equation of any line that is y = 2x – 6 + 5 parallel to the given line AND perpendicular to the y = 2x – 1 given line. (4 points each) -2x + y = -1 6. 2x + 5y = - 10 2x – y = 1 -2x -2x Graph a) y = 2x + 4 (Original equation) 5y = - 2x – 10 Graph b) y = 2x – 1 (New equation) 5 5 Check to be sure equations lines on graph are parallel 2 y = - /5 x – 2 as confirmation. 2 1 m1 = - /5 11. A line that is perpendicular to the line y = /2 x – 5, 2 || slope: y = - /5 x + # and passes through the point (2, -3) 5 slope: y = /2 x + # m = 2, (2, - 3) 7. 7x – 4y = 12 y = 2(x – 2) – 3 -7x -7x y = 2x + 4 – 3 - 4y = - 7x + 12 y = 2x + 1 -4 -4 -2x + y = 1 7 2x – y = -1 y = /4 – 3 1 7 Graph a) y = /2 x – 5 (Original equation) m1 = /8 7 Graph b) y = 2x + 1 (New equation) || slope: y = /4 x + # Check to be sure equations lines on graph are perpendicular as confirmation. Itg2 U2 Qz1 - Quiz 1 Fall 2011 For each problem below, write the equation of the line Integrated Math 2 – Unit 2 Quiz – Parallel/Perpendicular in all three forms. GRAPH BOTH LINES to check your For questions 1-4 below, determine if the lines are parallel ( || ), answers. (7 points each) perpendicular ( ), or neither and explain why. (3 points each) 8. A line that passes through the point (3, 7) and is 1. y = 2x – 1 and y = - 3(x – 1) – 4 parallel to y = 2x – 3 m1 = 2 m2 = - 3 m = 2, (3, 7) Therefore slopes are neither || nor y = 2(x – 3) + 7 3 3 y = - /4 x – 6 + 7 2. - 2x + 3y = -12 and y = - /2 x + 7 3y = 2x – 12 y = 2x + 1 2 -2x + y = -1 y = /3 x – 4 2 3 2x – y = 1 m1 = /3 m2 = - /2 Therefore slopes are to each other Graph a) y = 2x – 3 (Original equation) Graph b) y = 2x + 1 (New equation) 3 3 3. y = /4 (x – 8) + 1 and y = /4 x – 1 Check to be sure equations lines on graph are parallel 3 3 m1 = /4 m2 = /4 as confirmation. Therefore slopes are ||slopes to each other 9. A line that passes through the point (-2, -4) and is 1 4. - 2x + y = 3 and y = /2 x – 3 perpendicular to the point y = -2x – 6 y = 2x + 3 1 1 m = /2 , (-2, - 4) m1 = 2 m2 = /2 1 y = /2 (x + 2) – 4 Slopes are neither || nor (Although the slopes are 1 y = /2 x + 1 – 4 reciprocals of each other they are not the opposite 1 y = /2 x – 3 signs. (The sign did not change) 2y = x – 6 -x + 2y = - 6 5. a) What does opposite reciprocal mean? (2 points)
b) What types of slopes does it refer to? x – 2y = 6 Graph a) y = - 2x – 6 (Original equation) Slopes that are opposite reciprocals are slopes. 1 Graph b) y = /2 x – 3 (New equation) Opposite means the sign changes, so if one slope sign Check to be sure equations lines on graph are is positive the other will be negative or vice versa. perpendicular as confirmation. The term reciprocal means the numerator and 10. A line that is parallel to the line y = - 1/ x + 1, and denominator switch so the number that was on top is 3 passes through the point (9, 3) now on bottom and vice versa. 1 m = - /3 , (9, 3) 1 Rewrite each equation below in slope-intercept y = - /3 (x – 9) + 3 1 form. Then write the equation of any line that is y = - /3 x + 3 + 3 1 parallel to the given line AND perpendicular to the y = - /3 x + 6 given line. (4 points each) 3y = - x + 18 6. 2x + 3y = 15 x + 3y = 18 1 -2x -2x Graph a) y = - /3 x + 1 (Original equation) 1 3y = - 2x + 15 Graph b) y = - /3 x + 6 (New equation) 3 3 Check to be sure equations lines on graph are parallel 2 y = - /3 x + 5 as confirmation. 2 1 m1 = - /3 11. A line that is perpendicular to the line y = /2 x + 3, 2 || slope: y = - /3 x + # and passes through the point (4, 0) 3 slope: y = /2 x + # m = 2 , (4, 0) 7. 5x – 3y = - 9 y = 2(x – 4) – 0 -5x -5x y = 2x – 8 - 3y = - 5x – 9 -2x + y = - 8 -3 -3 2x – y = 8 5 1 y = /3 + 3 Graph a) y = /2 x + 3 (Original equation) 5 m1 = /3 Graph b) y = 2x – 8 (New equation) 5 Check to be sure equations lines on graph are || slope: y = /3 x + # 3 perpendicular as confirmation. slope: y = - /5 x + # 1 Itg2 U2 WS2.5 Day 1 Graphing 5. y = 3(x – 1) + 4 and y = /2 x + 1 1. What does the solution look like on a graph for a y = 3x – 3 + 4 system of equations? y = 3x + 1 A solution on a graph is the place where both lines intersect. For each system of equations below, find the solution by graphing. Write your answer as an ordered pair. 2. y = x and y = - x + 2
Solution: (0, 1) 6. y = 2(x + 3) – 5 and y = - 3x – 9 y = 2x + 6 – 5
Solution: (1, 1) y = 2x + 1 3. y = 2x – 6 and y = - 2x – 2
Solution: (1, - 4) 7. y = 2x – 1 and y = - x + 8 4. y = - x + 1 and y = 3x + 5
Solution: (- 1, 2 ) Solution: (3, 5) 8. y = (x – 4) + 2 and y = - 3x + 2 Itg2 U2 WS2.6 Day 2 Graphing y = x – 2 1. What does the solution look like on a graph for a system of equations with no solutions? If linear equations on a graph do not intersect, then there is no solution. This situation only happens when the two equations are parallel. 2. What does the solution look like on a graph for a system of equations with infinite solutions? If linear equations on a graph are in fact the same equation, then there are an infinite number of solutions. The solution to this system of equations is in fact the equation of the line. For each system of equations below, find the solution by graphing. Write your answer as an ordered pair. 1 3. y = /2 x – 3 and x – 2y = 6 – x – x
- 2y = - x + 6 Solution: ( 1, - 1) - 2 - 2 1 y = /2 x – 3 1 3 9. y = /2 x – 3 and y = /2 x – 1 Infinite Solutions since the lines are the same line
1 Solution: y = /2 x – 3 4. y = 2x – 6 and -2x + y = 3 Solution: (-2, - 4) + 2x + 2x y = 2x + 3 No Solution: Lines have the same slope, but have different y-intercepts thus they are parallel
1 1 5. y = - x + 1 and y = /2 x + 4 8. y = - x + 6 and y = /2 x + 3
Solution: (- 2, 3) 9. y = (x – 1) – 5 and y = x – 2 6. y = 2(x – 4) + 3 and -2x + y = 1 y = x – 6 y = 2x – 8 + 3 y = 2x + 1 No Solution: Lines have the same slope, but have y = 2x – 5 different y-intercepts thus they are parallel No Solution: Lines have the same slope, but have different y-intercepts thus they are parallel
10. 4x + 3y = 12 and 2x – 3y = 6 3y = - 4x + 12 - 3y = - 2x + 6 7. y = 3x + 3 and 6x – 2y = - 6 3 3 - 3 - 3 - 2y = - 6x – 6 4 2 y = - /3 x + 4 y = /3 x – 2 y = 3x – 3 No Solution: Lines have the same slope, but have different y-intercepts thus they are parallel
Solution: (3, 0)
Itg2 U2 WS2.7 Day 1 Substitution 5. x = 3y – 2 and -x + 4y = 4 1. What will indicate to you that you should be using - (3y – 2) + 4y = 4 substitution to solve a system of equations? - 3y + 2 + 4y = 4 Whenever one system of the equations has x or y y + 2 = 4 by itself equal to something else then substitution – 2 – 2 is easy to use. y = 2 Solve using substitution. x = 3(2) – 2 y = 6 – 2 2. y = 2x – 6 and 3x + 2y = 9 y = 4 3x + 2(2x – 6) = 9 (4, 2) 3x + 4x – 12 = 9 7x – 12 = 9 6. x + y = - 9 and x = 2y + 12 + 12 (2y) + y = - 9 7x = 21 3y = - 9 7 7 3 3 x = 3 y = - 3 y = 2x – 6 x = 2(- 3) y = 2(3) – 6 y = - 6 y = 6 – 6 (- 6, - 3) y = 0 7. y = 2x – 8 and x = - 3y – 3 (3, 0) y = 2(- 3y – 3) – 8 y = - 6y – 6 – 8 3. 3x + 4y = 8 and y = 2x + 13 y = - 6y – 14 3x + 4(2x + 13) = 8 + 6y + 6y 3x + 8x + 52 = 8 7y = - 14 11x + 52 = 8 7 7 – 52 – 52 y = - 2 11x = - 44 x = - 3(- 2) – 3 11 11 y = 6 – 3 x = - 4 y = 3 y = 2x + 13 (3, - 2) y = 2(- 4) + 13 8. x = - 3y + 16 and y = - 2x + 7 y = - 8 + 13 x = - 3(- 2x + 7) + 16 y = 5 x = 6x – 21 + 16 (- 4, 5) x = 6x – 5 – 6x – 6x 4. 3y – 2x = 11 and y = 9 – 2x -5x = - 5 3(9 – 2x) – 2x = 11 -5 -5 27 – 6x – 2x = 11 x = 1 27 – 8x = 11 y = - 2(1) + 7 – 27 – 27 y = - 2 + 7 - 8x = - 16 y = 5 - 8 - 8 (1, 5) x = 2 y = 9 – 2x 9. y = - 2x – 14 and y = x + 10 y = 9 – 2(2) (x + 10) = -2x – 14 y = 9 – 4 + 2x - 10 + 2x - 10 y = 5 3x = - 24 (2, 5) 3 3 x = - 8 y = (- 8) + 10 y = 2 (- 8, 2)
Itg2 U2 WS2.8 Day 2 Substitution 7. y = x – 9 and x = 2y + 4 1. What does it mean if you get a solution of 3 = 3 x = 2(x – 9) + 4 when doing substitution? Explain. x = 2x – 18 + 4 Infinite Solution: Lines are the same x = 2x – 14 – 2x – 2x 2. What does it mean if you get a solution of -2 = 5 - x = - 14 when doing substitution? Explain. x = 14 No Solution: Lines are parallel y = (14) – 9 Solve using substitution. y = 5 3. y = x + 13 and 2x – y = - 20 (14, 5) 2x – (x + 13) = - 20 2x – x – 13 = - 20 8. 3x = 5 – y and y = - 3x + 1 x – 13 = - 20 3x = 5 – (- 3x + 1) + 13 + 13 3x = 5 + 3x – 1 x = -7 0 = 4 y = (-7) + 13 No Solution: Lines are parallel y = 6 9. x = - 5y – 1 and x = 3y – 33 (-7, 6) (- 5y – 1) = 3y – 33 – 3y + 1 – 3y + 1 4. x = 3y – 2 and 6y = 2x + 36 - 8y = - 32 6y = 2(3y – 2) + 36 - 8 - 8 6y = 6y – 4 + 36 y = 4 0 = 32 x = - 5(4) – 1 No Solution: Lines are parallel x = -20 – 1 Proof: Find slope intercept of both equations x = -21 3y – 2 = x and 6y = 2x + 36 (-21, 4) 2 3y = x + 2 y = /6 x + 6 1 1 y = /3 x + 2 y = /3 x + 6 10. y = - x + 5 and y = 2x – 34 (- x + 5) = 2x – 34 2 5. y = - /3 x + 1 and 2x + 3y = 3 – 2x– 5 – 2x – 5 2 2x + 3(- /3 x + 1) = 3 - 3x = - 39 2x – 2x + 3 = 3 - 3 - 3 0 = 0 x = 13 Infinite Solution: Lines are the same Proof: Find slope intercept of both equations y = - (13) + 5 2 y = - /3 x + 1 2x + 3y = 3 y = - 8 3y = - 2x + 3 (13, - 8) 2 y = - /3 x + 1
6. x = -2y + 4 and 6y + 3x = 12 6y + 3 (-2y + 4) = 12 6y – 6y + 12 = 12 0 = 0 Infinite Solution: Lines are the same Itg2 U2 WS2.9 Day 1 Elimination 6. 4x – 3y = - 1 and 3x + y = 9 Solve by elimination 3(3x + y = 9) (common denominator for y’s = 3) 1. Describe a problem that would be easiest to solve by 4x – 3y = - 1 elimination. (What form are these problems in?) 9x + 3y = 27 When the linear equation is in Standard form then 13x = 26 elimination is usually best to solve the system. 13 13 2. 3y – 2x = 11 and y + 2x = 9 x = 2 3y – 2x = 11 3(2) + y = 9 y + 2x = 9 (x’s already cancel) 6 + y = 9 4y = 20 – 6 – 6 4 4 y = 3 (2,3) y = 5 7. 2x + 5y = 4 and 3x – 10y = -29 5 + 2x = 9 2(2x + 5y = 4) (common denominator for y’s = 10) – 5 – 5 4x + 10y = 8 2x = 4 3x – 10y = -29 2 2 7x = - 21 x = 2 (2, 5) 7 7 3. 2x + 3y = -1 and 5x – 3y = 29 x = -3 2x + 3y = -1 5x – 3y = 29 (y’s already cancel) 2(-3) + 5y = 4 7x = 28 - 6 + 5y = 4 7 7 + 6 + 6 x = 4 5y = 10 2(4) + 3y = -1 5 5 8 + 3y = -1 y = 2 (-3, 2) – 8 – 8 8. 3x + 4y = 8 and 4x – 2y = -26 3y = -9 2(4x – 2y = -26) (common denominator for y’s = 4)
3 3 3x + 4y = 8 y = -3 (4, -3) 8x – 4y = -52 4. 4x + 5y = 33 and - 4x – 3y = -23 11x = - 44 4x + 5y = 33 11 11 - 4x – 3y = -23 (x’s already cancel) x = -4 2y = 10 2 2 3(-4) + 4y = 8 y = 5 -12 + 4y = 8 4x + 5(5) = 33 + 12 + 12 4x + 25 = 33 4y = 20 – 25 – 25 4 4 4x = 8 y = 5 (-4, 5) 9. 2x + 5y = 11 and 3x – 4y = 5 4 4 x = 2 (2, 5) 3(2x + 5y = 11) 5. 5x – 3y = 6 and 2x + 3y = 15 -2(3x – 4y = 5) (common denominator for x’s = 6) 5x – 3y = 6 6x + 15y = 33 2x + 3y = 15 (y’s already cancel) - 6x + 8y = - 10 7x = 21 23y = 23 7 7 23 23 x = 3 y = 1 2(3) + 3y = 15 2x + 5(1) = 11 6 + 3y = 15 2x + 5 = 11 – 6 – 6 – 5 – 5 3y = 9 2x = 6 3 3 2 2 y = 3 (3, 3) x = 3 (1, 3) Itg2 U2 WS2.10 Day 2 Elimination y = 4 (5, 4) Solve by elimination 7. 2x + y = 8 and 4x + 2y = 12 1. When you get a solution of 4=4 when solving by -2(2x + y = 8) (So that y’s will cancel) elimination, what does the graph of the equations look 4x + 2y = 12 like? Explain. Infinite Solution: Lines are the same - 4x – 2y = - 16 4x + 2y = 12 2. When you get a solution of -2 = 2 when solving by 0 = - 4 elimination, what does the graph of the equations look like? Explain. No Solution: Lines are parallel No Solution: Lines are parallel 8. 2x + 5y = 11 and 3x – 4y = 5 Solve by using substitution. 3. x + y = 4 and 2x + 2y = 4 4(2x + 5y = 11) (common denominator for y’s = 20) 5(3x – 4y = 5) -2(x + y = 4) (So that x’s will cancel) 8x + 20y = 44 2x + 2y = 4 15x – 20y = 25 - 2x – 2y = - 8 23x = 69 2x + 2y = 4 23 23 0 = - 4 x = 3 No Solution: Lines are parallel 2(3) + 5y = 11 4. 2x + 14y = 10 and x + 7y = 5 6 + 5y = 11 2x + 14y = 10 - 6 - 6 -2(x + 7y = 5) 5y = 5 0 = - 4 5 5 No Solution: Lines are parallel y = 1 (3, 1) 5. 6x – 5y = 31 and 3x + 2y = 20 9. 3x + 2y = 12 and 5x – 3y = 1 6x – 5y = 31 3(3x + 2y = 12) (common denominator for y’s = 6)
-2(3x + 2y = 20) (common denominator for x’s) 2(5x – 3y = 1) 6x – 5y = 31 9x + 6y = 36 - 6x – 4y = - 40 10x – 6y = 2 - 9y = - 9 19x = 38 - 9 - 9 19 19 y = 1 x = 2 3x + 2(1) = 20 3(2) + 2y = 12 3x + 2 = 20 6 + 2y = 12 – 2 – 2 - 6 - 6 3x = 18 2y = 6 3 3 2 2 x = 6 (1, 6) y = 3 (2, 3) 6. 2x – 3y = - 2 and 4x + y = 24 10. 6x – 3y = 12 and 2x – y = 4 2x – 3y = - 2 6x – 3y = 12 (common denominator for y’s = 3) 3(4x + y = 24) (So that y’s will cancel) -3(2x – y = 4)
2x – 3y = - 2 6x – 3y = 12 12x + 3y = 72 - 6x + 3y = - 12 14x = 70 0 = 0 14 14 Infinite Solution: Lines are the same x = 5 4(5) + y = 24 20 + y = 24 - 20 - 20 Itg2 U2 WS2.11 5. 5x – y = 8 and x = 10 – 4y Integrated Math 2 – all 3 methods 5 (10 – 4y) – y = 8 1. What does the solution of a system of equation look 50 – 20y – y = 8 like on a graph? As an answer? 50 – 21y = 8 A solution on a graph is the place where both lines - 50 - 50 intersect. - 21y = - 42 Solve each system of equations below by graphing. - 21 - 21 1 1 y = 2 2. y = /2 x – 3 and y = /2 (x – 8) + 1 1 x = 10 – 4(2) y = /2 x – 4 + 1 1 x = 10 – 8 y = /2 x – 3 Infinite Solution: Lines are the same x = 2 (2, 2)
Solve by using elimination. 6. 2x – 8y = -18 and x + 8y = 15 2x – 8y = -18 (common denominator for y’s = 8) x + 8y = 15 3x = - 3 3 3 x = - 1 (- 1) + 8y = 15 + 1 + 1 8y = 16 8 8 y = 2 (- 1, 2) 3. y = 3x - 3 and y = 3x + 2 7. 2x + 3y = 2 and - 5x + 2y = 33 No Solution: Lines are parallel 5(2x + 3y = 2) (common denominator for x’s = 10) 2(- 5x + 2y = 33) 10x + 15y = 10 - 10x + 4y = 66 19x = 76 19 19 x = 4 2(4) + 3y = 2 8 + 3y = 2 - 8 - 8 3y = - 6 3 3 y = - 2 (4, - 2)
Solve each system of equations below by using substitution. 4. y = 4x – 2 and 6x – 2y = - 2 6x – 2(4x – 2) = - 2 6x – 8x + 4 = - 2 - 2x + 4 = - 2 - 4 - 4 - 2x = - 6 - 2 - 2 x = 3 y = 4(3) – 2 y = 12 – 2 y = 10 (3, 10)
Itg2 U2 Unit 2 Review for Test 5. 2x + 2y = 4 1. What two things do you know about parallel lines? – 2x – 2x Create your own pair of parallel lines and graph them. 2y = - 2x + 4 The two things I know about parallel lines are: 2 2 a) They have the same slope with different y-int. y = - x + 2 b) The two lines will never intersect. Solve each system of equations below by graphing. 1 c) y = 2x + 1 and y = 2x – 5 Lines are parallel 6. y = 3x – 6 and y = /2 x + 4
2. What two things do you know about perpendicular Solution: (4, 6) 1 lines? Create your own pair of parallel lines and graph 7. y = /2 x + 5 and y = - 2x – 5 them. The two things I know about perpendicular lines are: a) The slopes are opposite reciprocals of each other. b) The two lines will intersect at a right angle (90 0). c) y = x + 0 and y = - x + 2 Lines are parallel
Solution: (- 4, 3) 8. y = 2x – 4 and y = 2x + 3 Lines are parallel therefore No Solution
Put the following in Slope-Intercept form (Solve for y) 3. - 3x + y = - 2 + 3x + 3x y = 3x – 2
4. 4x – 6y = 12 – 4x – 4x - 6y = - 4x + 12 - 6 - 6 2 y = /3 x – 2
Solve each of the systems of equations by substitution. 3 3 9. x = 5y – 2 and 2x – 2y = - 12 y = - 4 2(5y – 2) – 2y = - 12 Solution: (1, - 4) 10y – 4 – 2y = - 12 Use the data below to create a scatterplot. Then draw a 8y – 4 = - 12 line of best fit. Make sure to label your graph. + 4 + 4 8y = - 8 8 8 y = - 1 x = 5(-1) – 2 x = - 5 – 2 x = - 7 Solution: (- 7, - 1) 10. 3x – y = 18 and y = 2x – 13 3x – (2x – 13) = 18 3x – 2x + 13 = 18 x + 13 = 18 – 13 – 13 x = 5 y = 2(5) – 13 y = 10 – 13 y = - 3 (5, - 3) Solve by using elimination. 11. - 4x + 2y = 22 and 4x + 3y = 13 (Common denominator for x’s = 4) - 4x + 2y = 22 4x + 3y = 13 13. Pick two points from your line (not your data) and 5y = 35 write the equation of the line in all three forms. 5 5 m = (28) – (8) y = 7 (30) – (50) 4x + 3(7) = 13 20 4x + 21 = 13 = /- 20 – 21 – 21 = - 1 4x = - 8 a) y = - 1(x – 50) + 8 4 4 y = - x + 50 + 8 x = - 2 b) y = - x + 58 Solution: (- 2, 7) c) x + y = 58 12. 3x – 5y = 23 and 2x + 3y = - 10 14. Use the equation of the line that you just created to 3(3x – 5y = 23) (common denominator for y’s = 15) answer the following questions. 5(3x – 5y = 23) a) At what distance would you predict if there were
32 goals made? 9x – 15y = 69 y = - x + 58 x = Distance; y = Field goals 10x + 15y = - 50 (32) = - x + 58 19x = 19 – 58 – 58 19 19 - 28 = - x x = 1 x = 28 28 yards from field goal 2(1) + 3y = - 10 2 + 3y = - 10 b) How many field goals would you predict were – 2 – 2 made from a distance of 38 yards?? 3y = - 12 y = - x + 58 x = Distance; y = Field goals y = - (38) + 58 y = 20 20 goals
2 Itg2 U2 WS2.1 ½ (Class-Work) y = /5 x + 3 Parallel and Perpendicular Lines Ex2. 4x + 2y = 8 Indicate whether the following are || , Neither 2y = - 4x + 8
1. y = 5x – 2 and y = 5x + 1 || y = -2x + 4 || y = -2x + 4 1 1 || 1 2. y = /2 x – 4 and y = /2 x + 3 y = /2 x – 5
1 3. y = - 5x – 6 and y = /5 x + 5 Ex3. - 9x + 3y = 12 3y = 9x + 12 1 1 4. y = - /2 x – 8 and y = - /2 x + 7 || y = 3x + 4 || y = 3x – 2 5. y = 2x – 2 and y = 5x + 1 Neither 1 y = - /3 x + 7
1 6. y = 5x – 2 and y = - /5 x + 1 Ex4. 7x – 3y = 12 -3y = - 7x + 12 2 2 || 7. y = /5 x – 4 and y = /5 x + 3 -3 -3 7 y = /3 x – 4 5 6 8. y = - /6 x – 6 and y = /5 x + 5 || 7 y = /3 x + 9 1 1 3 9. y = - /2 x – 8 and y = /2 x + 7 Neither y = - /7 x + 2 ------10. y = 2x – 2 and y = -2x + 1 Neither 1) x + 6y = 12 -x -x 11. y = 5(x – 2) + 1 and y = 5(x + 3) + 6 || 6y = -x + 12 6 6 1 2 5 y = - /6 x + 2 12. y = /5(x + 2) + 7 and y = - /2 (x – 3) + 2
3 3 2) -2x + 3y = 9 13. y = - /4(x – 2) + 3 and y = - /4 (x + 3) – 3 || +2x +2x
1 3y = 2x + 9 14. y = 2(x – 2) + 2 and y = - /2 (x – 2) + 4 3 3 2 y = /3 x + 3 15. y = 3(x + 2) + 14 and y = 3(x + 2) – 3 || 3) 4x – 8y = 16 16. y = 5(x – 2) + 7 and y = 5(x – 2) + 5 || -4x -4x -8y = -4x + 16 2 2 17. y = /5 (x + 2) – 5 and y = /5 (x – 2) + 8 || -8 -8 1 y = /2 x - 2 6 5 18. y = - /5 (x – 2) + 4 and y = - /6 (x – 2) + 9 Neither 4) 2x + 3y = 15 1 1 19. y = - /2 (x – 2) – 3 and y = - /2 (x + 2) + 1 || 3y = -2x + 15 2 y = - /3 x + 5 1 20. y = 2(x – 2) + 2 and y = - /2 (x – 2) – 2 5) -x + 4y = 12 4y = x + 12 1 Changing equations into S-I form (Solve for y). y = /4 x + 3 Next write two equations: (a) || and (b) 6) -6x – 2y = 10 Ex1. -2y = 5x – 2 -2y = 6x + 10 2y = - 5x + 2 -2 -2 y = - 5/ x + 1 2 y = -3x - 5 || 5 y = - /2 x + 1
1 1 Itg2 U2 WS2.3 /2 6. (9, 3) y = - /3 x + 1 1 Integrated Math 2 – Parallel Lines WS #2-3 m = - /3 , (9, 3) 1 Find the equation of the line that passes through the given y = - /3(x – 9) + 3 point and is parallel to the given line. y = -3x + 3 + 3 1 Write the equation of the line in all three forms y = /3 x + 6 1. (3, 7) y = 2x – 3 3y = x + 18 A parallel slope means that the slope is the same. -x -x
m = 2 , (3, 7) -x + 3y = 18 y = 2(x – 3) + 7 x – 3y = -18 y = 2x – 6 + 7 2 y = 2 x + 1 7. (-27, -12) y = /3 x 2 -2x + y = 1 m = /3 , (-27, -12) 2 2x – y = -1 y = /3 (x + 27) – 12 2 y = /3 x + 18 – 12 2 2. (-2, 5) y = x + 2 y = /3 x + 6 m = 1 , (-2, 5) 3y = 2x + 18 y = 1(x + 2) + 5 -2x -2x y = x + 2 + 5 -2x + 3y = 18 y = x + 7 2x – 3y = -18 -x - x 3 -x + y = 7 8. (10, 3) y = /5 x – 1 3 x – y = - 7 m = /5 , (9, 3) 3 y = /5 (x – 10) + 3 3 3. (1, 4) y = -3x + 1 y = /5 x – 6 + 3 m = - 3 , (1, 4) y = 3/ x – 3 y = -3(x – 1) + 4 5 5y = 3x – 15 y = -3x + 3 + 4 -3x -3x y = - 3x + 7 -3x + 5y = -15 +3x +3x 3x – 5y = 15 3x + y = 7
4. (0, 2) y = 5x – 6
m = 5 , (0, 2) y = 5(x – 0) + 2 y = 5x + 2 y = 5x + 2 -5x -5x -5x + y = 2 5x – y = -2
1 5. (-6, 1) y = /2 x – 2 1 m = /2 , (-6, 1) 1 y = /2 (x + 6) + 1 1 y = /2 x + 3 + 1 1 y = /2 x + 4 2y = x + 8 -x -x -x + 2y = 8 x – 2y = -8 Itg2 U2 WS2. B EXTRA PRACTISE (Needs to be fixed up) 6 5 = /5 + b 1) A line contains the points (3, -1) and (-1, 2). Another 5 1 4 /5 = 1 /5 + b line graphed in the same coordinate plane contains 1 1 – 1 /5 – 1 /5 the points (2, 0) and (-2, 3). 4 3 /5 = b a) How do these two lines relate 3 4 to each other? y = - /5 x + 3 /5 b) Write the equation of each 2. A line contains the points (7, 3) and (-1, -4). line in any of the three forms. Find the equation of the line. m1 = (- 1) – (2) m2 = (0) – (3) = ( 3) – (- 4) (3) – (-1) (2) – (-2) ( 7) – (- 1) 3 3 = - /4 = - /4 = 3 + 4 3 3 7 + 1 y1 = - /4(x – 3) – 1 y2 = - /4(x – 2) + 0 7 3 9 4 3 6 = /8 y = - /4 x + /4 – /4 y = - /4 x + /4 3 5 3 3 y = mx + b y = - /4 x + /4 y = - /4 x + /2 7 y = 3 5 y = ( /8) x + b - /4 x + /4 7 (3) = ( /8)(7) + b Therefore the two lines are parallel, 49 3 = /8 + b since they have the same slope and different 1 3 = 7 /8 + b y-intercepts 1 1 – 7 /8 – 7 /8 1 2) A line contains the points (0, -2) and (1, 3). Another - 4 /8 = b 7 1 line graphed in the same coordinate plane contains y = /8 x – 4 /8 the points (3, -1) and (-2, 0). How do these two lines 3. A line contains the points (4, -3) and (8, -1). relate to each other? Find the equation of the line.
m1 = ( - 2) – (3) m2 = ( - 1) – (0) = (- 3) – (- 1)
(0) – ( 1) (3) – (- 2) ( 4) – ( 8) - 5 - 1 = /- 1 = /5 = - 3 + 1 = 5 - 4 Therefore the two lines are perpendicular, = - 2 since the slopes are the opposite reciprocal of - 4 each other. 1 = /2 3) A line contains the points (0, -1) and (-1, 2). Another y = mx + b 1 line graphed in the same coordinate plane contains y = ( /2) x + b 1 the points (2, 0) and (-2, 3). How do these two lines (- 3) = ( /2)(8) + b relate to each other? - 3 = 4 + b m1 = ( - 1) – (2) m2 = ( 0) – (3) - 4 - 4 (0) – (- 1) (2) – (- 2) - 7 = b - 3 - 3 1 = / 1 = /4 y = /2 x – 7 = - 3 Therefore the two lines will intersect, but they 2) Write the equation of a line in slope-intercept form: are neither perpendicular nor parallel. (a) parallel and (b) perpendicular to the line: 4x - 2y = 8 and contains the point (-6, 2). 1. A line contains the points (-2, 5) and (3, 2). Solve both: (a) mathematically and (b) graphically. Find the equation of the line. (a) Mathematical Method - 4x + 2y = - 8 (Make y positive by multiplying by -1) m = ( 5 ) – ( 2 ) + 4x + 4x (Eventually get in the form: y = mx + b)
(- 2) – (3) 2y = 4x – 8 3 = - /5 2 2 y = 2x – 4 y = mx + b 3 Parallel Slope Perpendicular Slope y = (- /5) x + b 3 y = 2x + b y = - ½ x + b [Substitute in (–6,2)] (5) = (- /5)(- 2) + b (2) = 2(-6) + b (2) = - ½ (-6) + b Parallel Slope Perpendicular Slope 2 3 2 = - 12 + b 2 = 3 + b y = - /3 x + b y = /2 x + b [Substitute in (6,4)] + 12 + 12 _ -3 -3 _ 2 3 (4) = - /3(6) + b (4) = /2 (6) + b 14 = b -1 = b 4 = - 4 + b 4 = 9 + b y = 2x + 14 y = - ½ x – 1 + 4 + 4 _ - 9 - 9 _ (b) Graphic Method 8 = b - 5 = b 2 3 y = - /3 x + 8 y = /2 x – 5
Itg2 U2 WS2. B EXTRA PRACTISE Integrated Math 2 – Solve by elimination WS #2-9b Solve the following system of equations by elimination
1. 6x – 3y = 12 2x + 2y = 4 (-3)
6x – 3y = 12 (1 Step) -6x – 9y = -12 - 12y = 0 -12 -12 y = 0 2x + 2(0) = 4 2x = 4 2 2 x = 2 (2,0)
2. 3x + 2y = 13 (-2) 4x + 4y = 24 3) Write the equation of a line in slope-intercept form: -6x – 4y = -26 (1 Step) (a) parallel and (b) perpendicular to the line: 4x + 4y = 24 3x - y = - 2 and contains the point (1, 3). - 2x = -2 Solve mathematically only -2 -2 - 3x + y = 2 (Make y positive by multiplying by -1) x = 1 + 3x + 3x (Eventually get in the form: y = mx + b) y = 3x + 2 3(1) + 2y = 13
Parallel Slope Perpendicular Slope 3 + 2y = 13 1 – 3 – 3 y = 3x + b y = - /3 x + b [Substitute in (1,3)]
1 2y = 10 (3) = 3(1) + b (3) = - /3(1) + b 2 2 1 3 = 3 + b 3 = - /3 + b y = 5 (1,5) 1 1 - 3 - 3 _ + /3 + /3 _ 1 0 = b 3 /3 = b y = 3x + 0 1 1 y = 3x y = - /3 x + 3 /3
4) Write the equation of a line in slope-intercept form: (a) parallel and (b) perpendicular to the line: 2x + 3y = 9 and contains the point (6, 4). Solve mathematically only 2x + 3y = 9 (Make y positive by multiplying by -1)
- 2 x - 2 x (Eventually get in the form: y = mx + b) 3y = - 2x + 9 3 3 2 y = - /3 x + 3 3. 5x + 2y = - 8 7. 2x – y = 1 (2) x + 7y = 5 (-5) 3x + 2y = 12
5x + 2y = - 8 (1 Step) -5x – 35y = -25 4x – 2y = 2 (1 Step) -33y = -33 3x + 2y = 12 -33 -33 7x = 14 y = 1 7 7 x = 2 x + 7(1) = 5 x + 7 = 5 3(2) + 2y = 12 – 7 – 7 6 + 2y = 12 x = - 2 (-2,1) – 6 – 6 2y = 6 4. 6x – 5y = 31 2 2 3x + 2y = 20 (-2) y = 3 (2, 3) 6x – 5y = 31 (1 Step) -6x – 4y = -40 8. 3x + 2y = 12 (3) - 9y = - 9 5x – 3y = 1 (2) - 9 - 9 9x + 6y = 36 (2 Steps) y = 1 10x – 6y = 2 3x + 2(1) = 20 19x = 38 3x + 2 = 20 19 19 – 2 – 2 x = 2 3x = 18 3(2) + 2y = 12 3 3 6 + 2y = 12 x = 6 (6, 1) – 6 – 6 2y = 6 5. 2x + 3y = -13 (2) 2 2 5x – 6y = 8 y = 3 (2, 3) 4x + 6y = -26 (1 Step) 5x – 6y = 8 9. 4x – 3y = 25 (3) 9x = - 18 -3x + 8y = 10 (4) 9 9 x = -2 12x – 9y = 75 (2 Steps) -12x + 32y = 40 2(-2) + 3y = -13 23y = 115 - 4 + 3y = -13 23 23 + 4 + 4 y = 5 3y = - 9 3 3 4x – 3(5) = 25 y = - 3 (-2, -3) 4x – 15 = 25 + 15 + 15 6. 2x – 3y = -2 4x = 40 4x + y = 24 (3) 4 4 2x – 3y = - 2 (1 Step) x = 10 (5, 10) 12x + 3y = 72 14x = 70 35 14 14 7 x = 5 4(5) + y = 24 20 + y = 24 – 20 – 20 y = 4 (5,4)