Problem Set 9 Increasing and Decreasing

Problem Set 9 – Increasing and Decreasing

Problem Set 9 –Increasing and Decreasing

9.1 In this section, we will study how a derivative gives us information about when a function is increasing or decreasing.

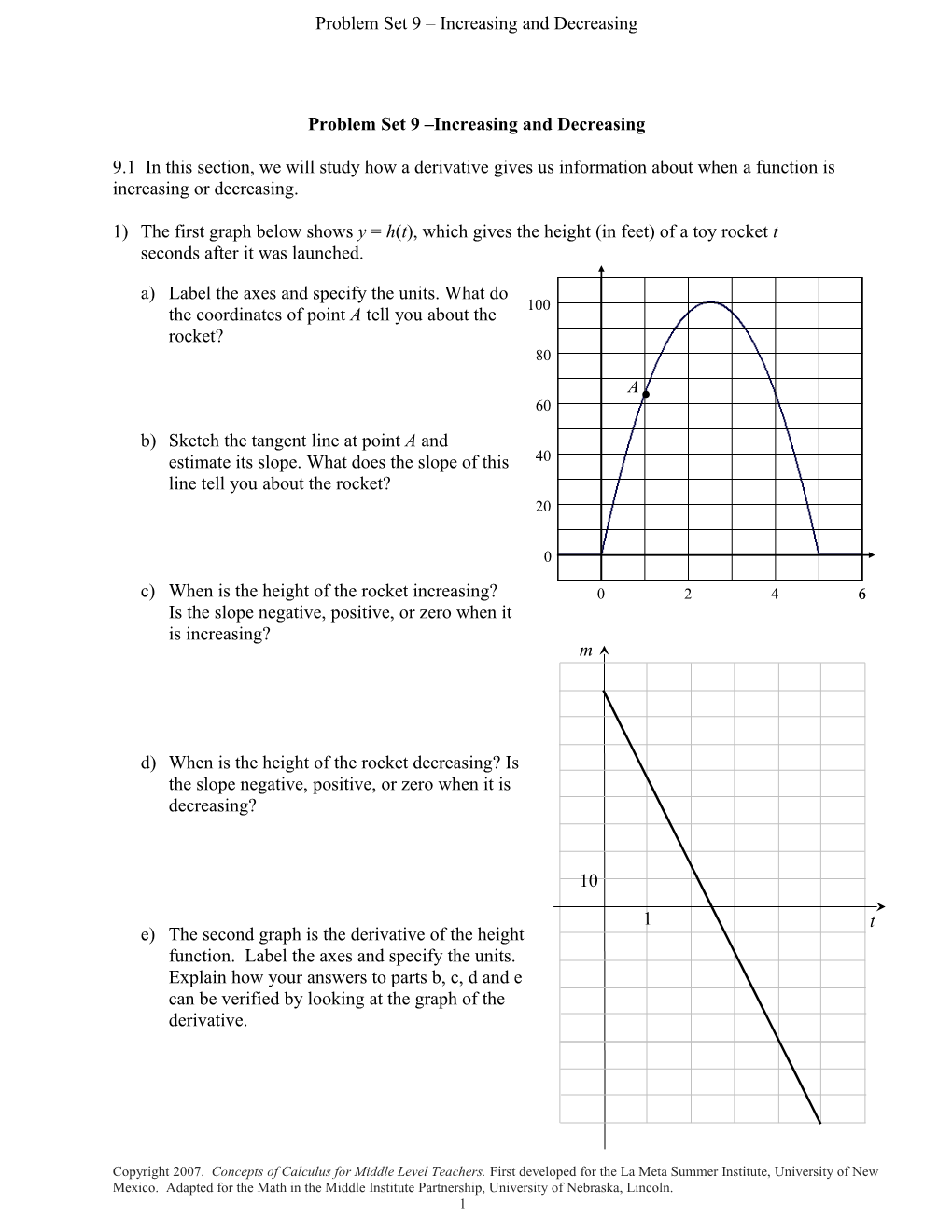
1) The first graph below shows y = h(t), which gives the height (in feet) of a toy rocket t seconds after it was launched.

a) Label the axes and specify the units. What do 100 the coordinates of point A tell you about the rocket? 80 A 60 b) Sketch the tangent line at point A and estimate its slope. What does the slope of this 40 line tell you about the rocket? 20

c) When is the height of the rocket increasing? 0 2 4 6 Is the slope negative, positive, or zero when it is increasing? m

d) When is the height of the rocket decreasing? Is the slope negative, positive, or zero when it is decreasing?

1 t e) The second graph is the derivative of the height function. Label the axes and specify the units. Explain how your answers to parts b, c, d and e can be verified by looking at the graph of the derivative.

Copyright 2007. Concepts of Calculus for Middle Level Teachers. First developed for the La Meta Summer Institute, University of New Mexico. Adapted for the Math in the Middle Institute Partnership, University of Nebraska, Lincoln. 1 Problem Set 9 – Increasing and Decreasing

2) Consider the function f (x)  x3  3x . a) Compute f '(x) , and find the roots of this polynomial.

b) Indicate the root(s) of the derivative on the graph of the derivative. y m

f (x)  x3  3x f '(x) c) On which intervals is the function f (x)  x3  3x increasing? Decreasing? How does the graph of f ' confirm this?

3) Consider the function f (x)  x3 . a) Compute f '(x) , and find the roots of this polynomial.

b) Indicate the root(s) of the derivative on the graph of the derivative. y m

f (x)  x3 f '(x) c) On which intervals is the function f (x)  x3 increasing? Decreasing? How does the graph of f ' confirm this?

4) This time we only have information about the derivative of the function f . From the graph of f ' , determine on which intervals the function f is increasing, decreasing, or neither.

5) An apartment complex has 250 apartments to rent. If they rent x apartments then their monthly profit, in dollars, is given by,

a) Calculate the derivative of this function and determine if the profit is increasing or decreasing for the following values of x. i. 225 apartments per month

ii. 180 apartments per month

b) The derivative tells you the rate of change of the profit. Interpret what the derivative means when x = 225 (this is just like interpreting slope).

c) Using the derivative to understand how small changes in the number of apartments rented per month affects the profit:

i. If 225 apartments are rented in a month, how much profit will be made?

ii. Use the answer to i) and the derivative from 5a to estimate the profit made when 226 apartments are rented in a month.

iii. Find the equation of the tangent line to the profit function at x = 225, and write your answer in the form y  mx  b .

iv. Roughly sketch both the graph of the profit function and the tangent line to the graph at x = 225. You may use your calculator to help with this.

v. Plot the points (226, P(226)) and (226, y(226)) on your graph, and explain what these two points represent.

vi. Using the ideas in i) and ii), estimate the profit when 224 apartments are rented per month.

Copyright 2007. Concepts of Calculus for Middle Level Teachers. First developed for the La Meta Summer Institute, University of New Mexico. Adapted for the Math in the Middle Institute Partnership, University of Nebraska, Lincoln. 4