Geometry-R Module 4

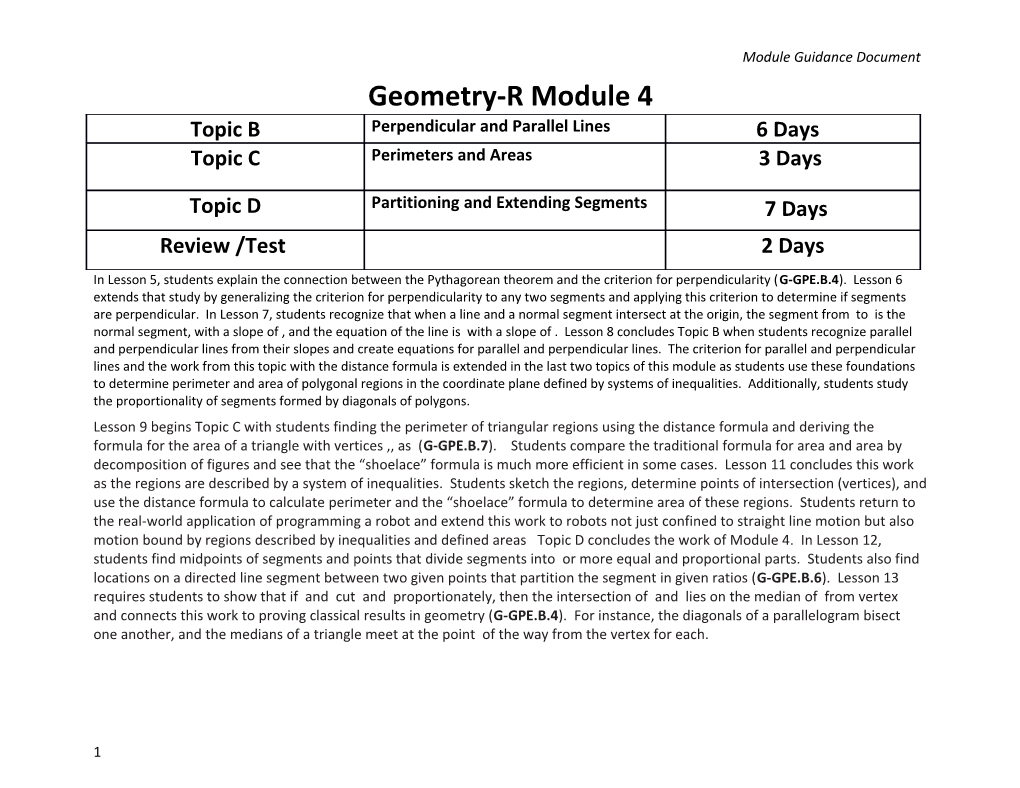
Module Guidance Document Geometry-R Module 4 Topic B Perpendicular and Parallel Lines 6 Days Topic C Perimeters and Areas 3 Days

Topic D Partitioning and Extending Segments 7 Days Review /Test 2 Days

In Lesson 5, students explain the connection between the Pythagorean theorem and the criterion for perpendicularity (G-GPE.B.4). Lesson 6 extends that study by generalizing the criterion for perpendicularity to any two segments and applying this criterion to determine if segments are perpendicular. In Lesson 7, students recognize that when a line and a normal segment intersect at the origin, the segment from to is the normal segment, with a slope of , and the equation of the line is with a slope of . Lesson 8 concludes Topic B when students recognize parallel and perpendicular lines from their slopes and create equations for parallel and perpendicular lines. The criterion for parallel and perpendicular lines and the work from this topic with the distance formula is extended in the last two topics of this module as students use these foundations to determine perimeter and area of polygonal regions in the coordinate plane defined by systems of inequalities. Additionally, students study the proportionality of segments formed by diagonals of polygons. Lesson 9 begins Topic C with students finding the perimeter of triangular regions using the distance formula and deriving the formula for the area of a triangle with vertices ,, as (G-GPE.B.7). Students compare the traditional formula for area and area by decomposition of figures and see that the “shoelace” formula is much more efficient in some cases. Lesson 11 concludes this work as the regions are described by a system of inequalities. Students sketch the regions, determine points of intersection (vertices), and use the distance formula to calculate perimeter and the “shoelace” formula to determine area of these regions. Students return to the real-world application of programming a robot and extend this work to robots not just confined to straight line motion but also motion bound by regions described by inequalities and defined areas Topic D concludes the work of Module 4. In Lesson 12, students find midpoints of segments and points that divide segments into or more equal and proportional parts. Students also find locations on a directed line segment between two given points that partition the segment in given ratios (G-GPE.B.6). Lesson 13 requires students to show that if and cut and proportionately, then the intersection of and lies on the median of from vertex and connects this work to proving classical results in geometry (G-GPE.B.4). For instance, the diagonals of a parallelogram bisect one another, and the medians of a triangle meet at the point of the way from the vertex for each.

1 Module Guidance Document

Suggested Lessons Big Idea Emphasize Important Concepts to Focus On: Sample Regents Module 4 Focus on the distance formula, the June 2015 # 09, 27, 31, 36 midpoint and partition of a August 2015 # 10, 15,22, 31, 33 TOPIC B segment. The focus should also be January 2016 # #2,18, 15,27 on the coordinate geometry and proving quadrilaterals Lesson 1 Lesson 1: Graphing Linear equations with two variable Use coordinates to prove simple geometric theorems algebraically. and systems of equations G-GPE.B.4 Use coordinates to prove simple geometric theorems algebraically. Teacher created For example, prove or disprove that a figure defined by four given materials Objective: I can graph linear equations and points in the coordinate plane is a rectangle; prove or disprove that systems of linear equations and I can identify the point lies on the circle centered at the origin and containing the solution(s) to systems of equations point . 2 G-GPE.B.5 Prove2F the slope criteria for parallel and perpendicular lines and Suggested Day(s): ( 1) use them to solve geometric problems (e.g., find the equation of a line parallel or perpendicular to a given line that passes through a Lesson 2 Lesson 2: Writing the equation of a line in slope given point). Teacher created intercept form and point – slope form G-GPE.B.6 Find the point on a directed line segment between two given points Materials that partitions the segment in a given ratio. Objective: Students will write the equations of G-GPE.B.7 Use coordinates to compute perimeters of polygons and areas of lines in slope- intercept and slope-point form ★ triangles and rectangles, e.g., using the distance formula. when two points are given, a graph is given, and the slope and one point is given Foundational Standards

Suggested Day(s): ( 1) Solve systems of equations.

1In preparation for Regents Exams, a trapezoid is defined as a quadrilateral that has at least one pair of parallel sides.

2Prove and apply (in preparation for Regents Exams).

Suggested Lessons Big Idea Emphasize Sample Regents Module 4 June 2015 # 09, 27, 31, 36 Lesson 5 in Lesson 3: Criterion for Perpendicularity A-REI.C.6 Solve systems of linear equations exactly and approximately (e.g., EngageNY with graphs), focusing on pairs of linear equations in two variables. Objective: Students explain the connection between the Pythagorean theorem and the criterion for perpendicularity Suggested day(s) : 1

Lesson 7 in Lesson 4 : Equations for Lines Using Normal Segments Engage Ny Objective: Students recognize a segment perpendicular to a line, with one of its endpoints on the line as a normal segment.

Students recognize that when a line and a normal segment intersect at the origin, the segment from to is the normal segment, with a slope of , and the equation of the line is with a slope of . Suggested Day(s): ( 1)

Lesson 8 Lesson 5 Parallel and perpendicular Lines in EngageNY Objective: Students recognize parallel and perpendicular lines from slope. Students create equations for lines satisfying criteria of the kind: “Contains a given point and is parallel/perpendicular to a given line.” Suggested Day(s): ( 2) Important concepts to focus on Topic C The focus will be using the distance formula to calculate perimeter and determine area of these regions.

Suggested Lessons Big Idea Emphasize Lesson 9 in Lesson 6: Perimeter and Area of Triangles in the EngageNy Cartesian plane Sample Regents Module 4 Objective: Students find the perimeter of a triangle in June 2015 # 09, 27, 31, 36 the coordinate plane using the distance formula. August 2015 # 10, 15,22, 31, 33 Students state and apply the formula for area of a January 2016 # #2,18, 15,27 triangle with vertices (0,0),(x1, y1), and (x2 , y2).

Suggested Day(s): ( 1)

Lesson 10 In Lesson 7: Perimeter and Area of Polygonal Enagageny Regions in the Plane

Objective: I can find the perimeter of a quadrilateral in the coordinate plane given its vertices and edges. I can find the area of a quadrilateral in the coordinate plane given its vertices and edges

Lesson 11- Lesson 8: Triangle inequality and types of optional triangles In Engageny Objective: Students find the perimeter of a triangle or quadrilateral in the coordinate plane given a description by inequalities. Students find the area of a triangle or quadrilateral in the coordinate plane given a description by inequalities by employing Green’s theorem. Suggested Day(s): ( 1 days )

Suggested Lessons Big Idea Emphasize Important concepts to focus on Topic D Sample Regents Module 4 June 2015 # 09, 27, 31, 36 The focus will be the midpoints of segmentsAugust and 2015 points # 10,that 15,22, divide 31, segments 33 into 3 or more equal and proportional parts andJanuary extend 2016 this concept# #2,18, prove15,27 classical results in geometry. Focus will also be on profs using coordinate geometry

Lesson 12 In Lesson 9: Midpoint and Partition Enagageny Objective: Students find midpoints of segments and points that divide segments into 3, 4, or more proportional, equal parts

Lesson 13 In Lesson 10: Analytic Proofs of Theorems Previously Enagageny Proved by Synthetic Means

Objective: Using coordinates, students prove that the intersection of the medians of a triangle meet at a point that is two-thirds of the way along each median from the intersected vertex. Using coordinates, students prove the diagonals of a parallelogram bisect one another and meet at the intersection of the segments joining the midpoints of opposite sides.

Suggested Lessons Big Idea Emphasize Teacher created Review of unit assessment Sample Regents Module 4 assessment June 2015 # 09, 27, 31, 36 Suggested Day(s): ( 2) August 2015 # 10, 15,22, 31, 33 January 2016 # #2,18, 15,27