Department of Electrical & Electronic Engineering

UNIVERSITY OF HONG KONG Department of Electrical & Electronic Engineering M.Sc.(Eng) in Building Services Engineering MEBS6002 2010 Lighting Engineering

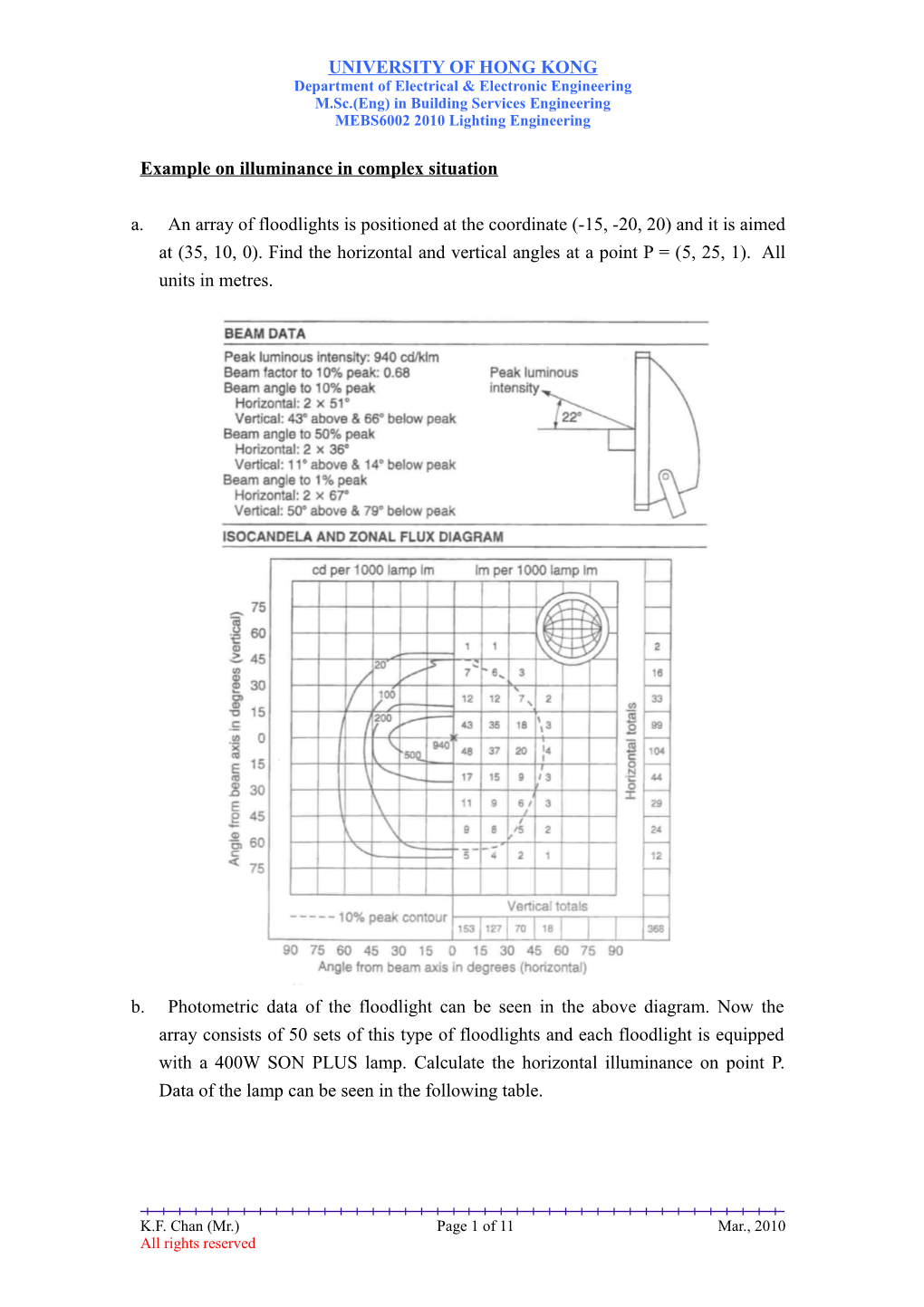
Example on illuminance in complex situation a. An array of floodlights is positioned at the coordinate (-15, -20, 20) and it is aimed at (35, 10, 0). Find the horizontal and vertical angles at a point P = (5, 25, 1). All units in metres.

b. Photometric data of the floodlight can be seen in the above diagram. Now the array consists of 50 sets of this type of floodlights and each floodlight is equipped with a 400W SON PLUS lamp. Calculate the horizontal illuminance on point P. Data of the lamp can be seen in the following table.

K.F. Chan (Mr.) Page 1 of 11 Mar., 2010 All rights reserved UNIVERSITY OF HONG KONG Department of Electrical & Electronic Engineering M.Sc.(Eng) in Building Services Engineering MEBS6002 2010 Lighting Engineering

c. If a camera is located at (10, 5, 2), calculate the illuminance at point P on a plane normal to the direction of the camera. d. Hence, calculate the luminance of a matt surface at point P on a plane normal to the direction of the camera. Given reflectance of the surface is 0.4.

ANSWER a). First of all, transfer the coordinate system such that the coordinate of the lamp becomes (0,0,0)

Thus in the new x’, y’, z’ coordinate L = (0,0,0) A = (50, 30, -20) P = (20, 45, -19)

Then, rotate the coordinate system such that point A is on the (u, w) plane

The angle of rotation is ' 1 y A 1 30 ξ  tan '  tan x A 50 ξ  30.96

Coordinate of point P in the new (u, v) system can be found by considering the following diagram

It can be seen from this diagram that up = x’p cos + y’p sin

vp = -[x’p sin - y’p cos]

wp = z’p

Therefore uP = 20cos 30.96° + 45sin30.96° = 40.3 vP = 45cos 30.96° - 20sin30.96° = 28.3

Also, uA = 50cos 30.96° + 30sin30.96° = 58.31 vA = 30cos 30.96° - 50sin30.96° = 0 naturally

It can be seen from the above diagram that vertical angle is

u u v  tan1( P )  tan1( A ) wP wA while horizontal angle is

 v  H  tan 1  P   2 2   u P  w P 

So, 40.3 58.31 v  tan 1 ( )  tan 1 ( ) 19  20  6.31O 28.3 H  tan 1 40.32  19 2  32.42

K.F. Chan (Mr.) Page 6 of 11 Mar., 2010 All rights reserved UNIVERSITY OF HONG KONG Department of Electrical & Electronic Engineering M.Sc.(Eng) in Building Services Engineering MEBS6002 2010 Lighting Engineering b) Now from the photometric data of the floodlight, it can be seen that at vertical angle and horizontal angle of 6.31o and 32.42o, the intensity of each floodlight is 500cd/klm. Also each 400W SON PLUS gives 54000lumens. An array of 50 such floodlights thus gives 500 x 54 x 50 = 1350000cd.

To find the horizontal illuminance on a surface facing upwards, we take the normal as

nz , the angle of incidence is given by

n PL cos  z H length PL

nz xL  x p nx  yL  y p ny  zL  z p nz   length PL z  z  L P 2 2 2 xL  x p   yL  y p   zL  z p 

20 1  15  52   20  252  20 12 19  52.78

o Thus  H  68.9 , and length LP is 52.78m

Therefore, horizontal illuminance on point P is 1350000 E  cos68.9o  174.4lux h 52.782

c) For camera at xC, yC, zC, the angle of incidence between LP and CP is given by vector PC vector PL cos     C length PClength PL

xC  x p nx  yC  y p ny  zC  z p nz xL  x p nx  yL  y p n y  z L  z p nz   2 2 2 2 2 2 xC  x p   yC  y p   zC  z p  xL  x p   yL  y p   z L  z p  x  x x  x  y  y y  y  z  z z  z   C p L p C p L p C p L p 2 2 2 2 2 2 xC  x p   yC  y p   zC  z p  xL  x p   yL  y p   z L  z p 

Therefore angle between the illumination vector and the camera vector can be found by

(10  5)(15  5)  (5  25)(20  25)  (2 1)(20 1) cos C  (10  5) 2  (5  25) 2  (2 1) 2 52.78 819 cos  C (20.64)(52.78)

 C  41.26 where 52.78m is the distance between the lamp, L, and the point to be illuminated, P.

Therefore illuminance on a plane through point P normal to the camera angle is 1350000 E  cos 41.26 (52.78) 2  364.3lux d) Luminance of the surface is given by E  0.4364.3    46.4 cd / m2

A spreadsheet can be prepared for multiple calculations:

Lamp Aiming Illuminated Camera point Point L A P C x -15.00 35.00 5.00 10.00 y -20.00 10.00 25.00 5.00 z 20.00 0.00 1.00 2.00

Iθ 1,350,000.00 cd ρ 0.4

x’ = x – xL 0.00 50.00 20.00 25.00

y’ = y – yL 0.00 30.00 45.00 25.00

z’ = z - zL 0.00 -20.00 -19.00 -18.00

o 1 y' A 30.96   tan x' A

y' 0.51 sin   A 2 2 x' A  y' A

x' 0.86 cos  A 2 2 x' A  y' A

u = x’cos ζ + y’sinζ 0.00 58.31 40.30 34.30 v = -[x’sinζ - y’cosζ] 0.00 0.00 28.30 8.57 w = z’ 0.00 -20.00 -19.00 -18.00 Vertical angle 6.31 o u u B  tan 1 ( P )  tan 1 ( A ) w P w A Horizontal angle 32.42 o  v  β  tan 1  P   2 2   u P  w P 

Length LP 2 2 2 0.5 = [(xP-xL) + (yP-yL) + (zP-zL) ]

52.78 m

Angle between illuminati on vector and aiming vector

 (x  x )(x  x )  (y  y )(y  y )  (z  z )(z  z )  θ  cos 1 P L A L P L A L P L A L   2 2 2 2 2 2   (x P  x L )  (y P  yL )  (z P  z L ) (x A  x L )  (y A  y L )  (z A  z L ) 

32.96 o

Camera angle to illuminati on vector   1 (x C  x P )(x L  x P )  (y C  y P )(y L  yP )  (z C  z P )(z L  z P )  θ c  cos  2 2 2 2 2 2   (x C  x P )  (y C  y P )  (z C  z P ) (x L  x P )  (y L  y P )  (z L  z P ) 

41.26 o

Angle of incidence   1 (z L  z P )  θ H  cos  2 2 2   (x L  x P )  (y L  yP )  (z L  z P ) 

68.90 o

Intensity at illuminating direction 1,350,000.00 cd

Horizontal illuminance at P I 174 .4 lux E  θ cosθ h LP 2 H

Illuminance at P on a surface normal to the direction of the camera

Intensity 364 . 3 lux  cosθ (length LP) 2 C

Luminance of horizontal surface at P with refectance ρ

2 = ρEh/π 22 .2 cd/m

Luminance of a surface with 46 . 4 cd/m2 refectance ρ at P normal to the direction of the camera