Math 9 Slope of a Line Segment Lesson 2-3

Math 9 Slope of a Line Segment Lesson 2-3 MOM (Atlantic) Page 100-101 Name SOLUTIONS

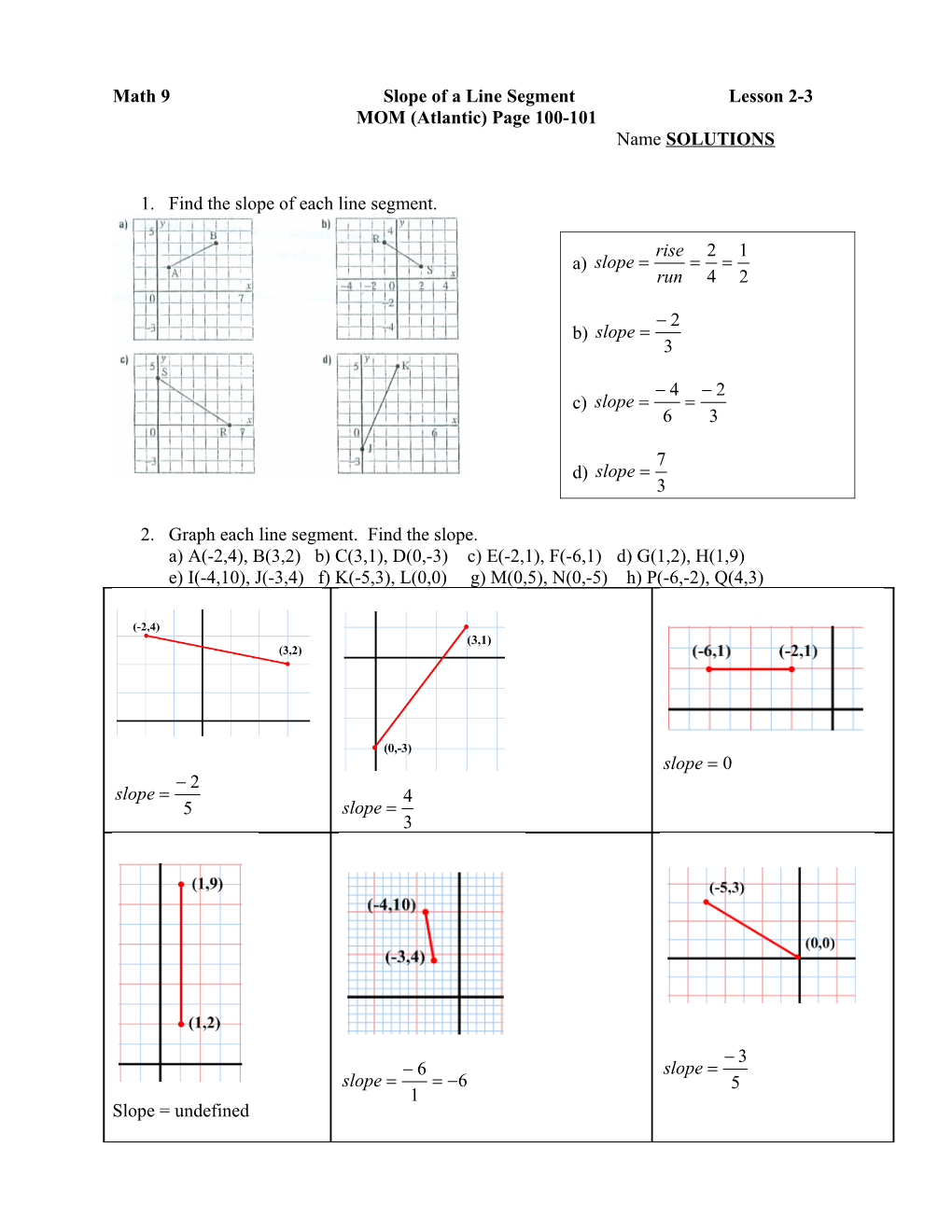
1. Find the slope of each line segment.

rise 2 1 a) slope    run 4 2

 2 b) slope  3

 4  2 c) slope   6 3

7 d) slope  3

2. Graph each line segment. Find the slope. a) A(-2,4), B(3,2) b) C(3,1), D(0,-3) c) E(-2,1), F(-6,1) d) G(1,2), H(1,9) e) I(-4,10), J(-3,4) f) K(-5,3), L(0,0) g) M(0,5), N(0,-5) h) P(-6,-2), Q(4,3)

slope  0  2 slope  4 5 slope  3

 3  6 slope  slope   6 5 1 Slope = undefined 5 1 slope   10 2

Slope = undefined

3. For each relation below:

a) Copy and complete the table of values. b) Graph the equation. c) What is the slope of any segment of the graph?

i) y = -3 + 4x ii) y = 2x - 5 x y x y 1 1 1 -3 2 5 2 -1 3 9 3 1 4 13 4 3 5 17 5 5

8 16 slope   2 slope   4 4 4 4. For each equation is exercise 3:

a) Is the relation linear? b) Explain how the table of values shows whether the relation is linear. c) Explain how the slope shows whether the relation is linear.

Yes because they are both There is a different y value In “A” for every 4 units up straight lines. for every x value. you go over 1 unit. This Also the y value is going up gives a straight line. by the same amount for In “B” for every 2 units up every x value. you go over 1 unit. This gives you also a straight line.

MOM (Atlantic) Page 104 Name SOLUTIONS

1. State the slope of each line. 2 a) slope   2 1

 3 b) slope  2

1 c) slope  2

2. State the slope of each line. 3 a) slope  2

5 b) slope   5 1

 6 c) slope   3 2 3. Draw a line through each point with each given slope.  3 1 a) A(-2, 1), slope 3 b) B(4,0), slope c) C(0,0), slope d) D(-1,-3), slope -4 2 4

4. Draw a line through B(3,2) with each slope. 1 a) 2 b) c) -3 d) 0 2 5. Draw a line through E(0,4) with each slope. Find the coordinates of 2 more points on each line.

1 1 a) 3 b) c) -2 d) 2 4 MOM (Atlantic) Page 105 Name SOLUTIONS 8. Draw the line through each pair of points. Find the coordinates of 2 more points on each line. a) E(2,3) and F(1,7) b) G(-4,7) and H(1,0) c) J(-6, -2) and K(5,8) d) L(-3,-7) and M(-4,-6)

9. Graph each set of points. i) A(0, 1), B(3,3), C(9,7) ii) A(-6, 1), B(-2, -1), C(4, -4) iii) A(8, 5), B(-2, 1), C(3,3) a) Find the slopes of AB, BC and AC. What do you notice? Explain whether this makes sense. b) Suppose D is another point on the line. What is the slope of AD? How do you know?

2  2 1 slopeAB  slopeAB   3 4 2 6 2  5 1 slopeAC   slopeAC   9 3 10 2 4 2  3 1 slopeBC   slopeBC   6 3 6 2 a) All the slopes are the same for each question. This makes sense because the slope should be the same on any one line.

b) If D was placed on the line, then AD would have the same slope as 2 all the others in the question slopeAB  5 because the slope of a line is the 4 2 same for all points on the line. slopeAC   10 5 2 slopeBC  5

11. A line has slope -1. It passes through the points C(q, 3) and D(4, -2). What is the value of q? Slope = -1

The value of q is -1

1 12. Two lines intersect at N(0,4). They have slopes of 2 and . Determine the coordinates 2 at which each line intersects the x-axis.