Boddeker's Mechanics Notes

Chapter 6 Outline: Circular Motion (w/Newton’s Laws) 6.1 Newton's Second Law Applied to 6.3 Motion in Accelerated Frames Uniform Circular Motion 6.4 Motion in the Presence of Resistive Forces 6.2 Non-uniform Circular Motion 6.5: Numerical Modeling in Particle Dynamics

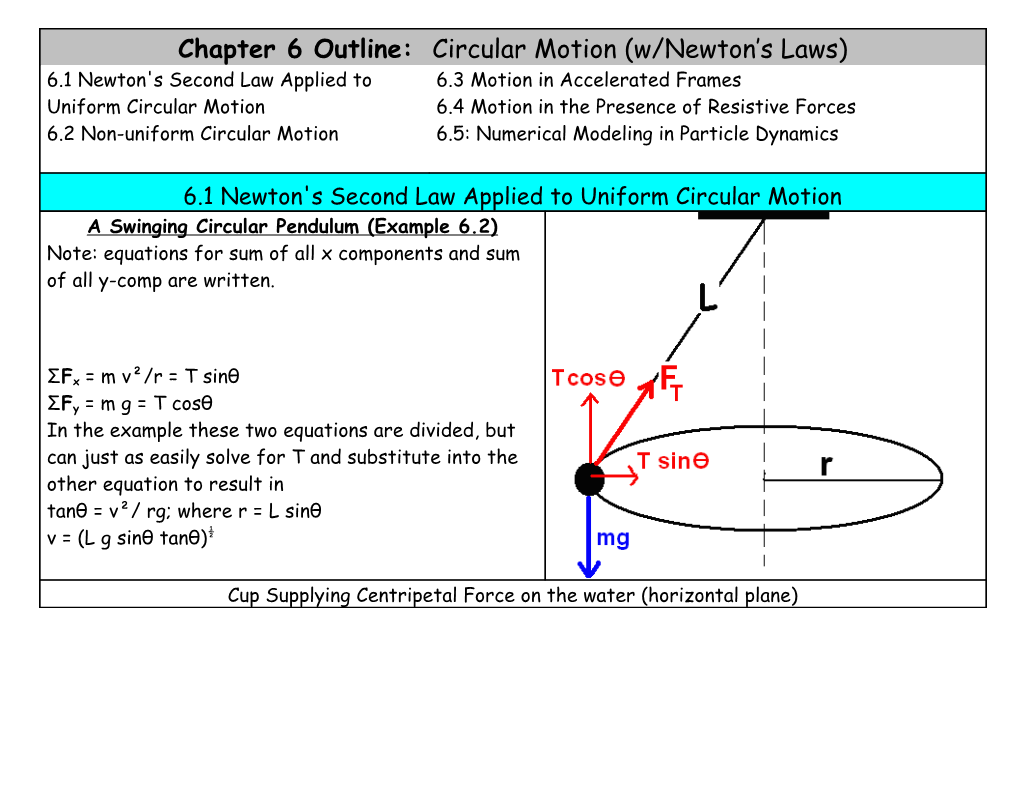
6.1 Newton's Second Law Applied to Uniform Circular Motion A Swinging Circular Pendulum (Example 6.2) Note: equations for sum of all x components and sum of all y-comp are written.

ΣFx = m v²/r = T sinθ

ΣFy = m g = T cosθ In the example these two equations are divided, but can just as easily solve for T and substitute into the other equation to result in tanθ = v²/ rg; where r = L sinθ v = (L g sinθ tanθ)½

Cup Supplying Centripetal Force on the water (horizontal plane) During lecture a cup of water was swung over my head in several different planes. How can you tell the tension in the string in this case? The key is to relate the y-comp and the x-comp of the Tension and set them equal.

FT-x = mv²/cosθr FT-y = mg/sinθ mv²/cosθr = mg/sinθ v = (g cotanθ/r)½

Demo: Centrifugal Hoops: ME-D-CH

Demo: Rotating Candles: ME-D-RC 6.2 Non-uniform Circular Motion Demo: Pail of Water: ME-D-PW Cup Supplying Centripetal Force on the water (verticle plane)

When I was swinging the cup of colored water I also spun the water in the vertical direction. How fast would the cup be moving if the tension went to a minimum at the top of it's path, Ttop = 0; where if any slower it wouldn't quite make it to the top of the path.

Normally near the top the Fcentrip = mg + T = mv²/r, except this time the Tension = 0 N, thus mg = mv²/r Thus velocity for the cup with blue water at the top of the path was (rg)½ = 2.8 m/s or about 6 mph. Rotating Cup with Water, Tension at Bottom When I was swinging the cup of colored water I also spun the water in the vertical direction. How fast would the cup be moving (tangential velocity) at the bottom of the path if the tension went to a minimum at the top of it's path, Ttop = 0;

In the earlier example at the top of its path T = 0 N , so mv²/r = mg but at the bottom of the path Fcentrip = T = mv²/r + mg, Thus velocity for the cup with blue water at the bottom of the path would be dependant upon the velocity at the top of the path and the work done upon the cup by gravity. So the Work = Δ ½mv² will give the addition velocity, and thus we can determine the Tension on the string.

mg(hmax - hmin) = Δ ½mv² g (1.6 m) = ½ (vf² - vi²)

32 m²/s² = (vf² - (2.8 m/s)²) vf = 6.3 m/s

T = mv²/r + mg = (60 * mass) N or you could say, 6 "g's" on the cup of water 6.3 Motion in Accelerated Frames Accelerating Van with Fuzzy Dice Perpendicular to Plane of the Ramp

What is the angle of the ramp if a van was accelerating down the ramp at the rate of 5 m/s² and fuzzy dice were hanging down perpendicular to the ceiling?

As you can see in the picture below. The force caused by the acceleration of the van was 5m and and gravity exerted a force of 10m. Thus the angle was sin θ = ma / mg θ = 30° Accelerating Cart Equals Accelerating Box-Block system

A cart was being accelerated with a force, F. On the cart was two blocks connected with a string. One block was hanging over the front of the cart as seen below. What is the force applied if the blocks do not move wrt to the cart. Thus the acceleration caused by this force must equal the acceleration of the block system so that T1 = T2

Since we have a free moving pulley…T1 = T2 F = (M + m1 + m2) a2

(and since the pulley isn’t moving) But a2 must equal a1 for the pulley (same string) so

T1 = m1a a2 = a1 = m2 g / m1

T2 = m2g F = (M + m1 + m2)* m2 g / m1 m1a = m2g

Thus a1 = m2 g / m1

Today we finally officially introduced Chapter 7 & 8 with the formal derivation of Work = Δ Kinetic Energy

6.4 Motion in the Presence of Resistive Forces AIR Friction We've already briefly mentioned that the resistive force in a medium like air is proportional to the square of the velocity. This maximum velocity is obviously dependant upon surface area exposed to the air (sky diver accelerates by diving), the density of the medium, and the shape of the object (sky spread out arms instead of pulling arms in to his/her sides). Thus giving us R = ½DρAv² where D vary's from 0.5 to 2 depending on shape. We know that at terminal velocity ½ mg = ½ DρAv² and solving for terminal velocity yields vT = (2mg / DρA)

Let's calculate the approximate vT for a sky diver of 80 kg in air with density of 1.29 kg/m³ with surface area of 0.65 m². As usual you can use 10 m/s² instead of 9.8 m/s² for accel due to gravity ½ vT = (2mg / D ρ A) ½ vT = (2*80*10 / 0.9*1.29*0.65) vT = = 52.3 m/s Remember on the first day of class where we made a general rule of thumb...about 2 mph is about 1 m/s

This means that the approximate vT of a sky diver is about 110 mph FResist = -b v Something to look forward to for next term Terminal Velocity

An dropping (or rising must include buoyant force, which is covered in a later chapter, see to the right) object's maximum velocity due to a resistance force by a particular medium

FW = -FR mg = -bv

The above force diagram shows that the weight vector is equal and in the opposite direction of the resistive force.

The rate of acceleration continually decreases as time progresses and an object approaches terminal velocity.

FNet = ma FNet = mg - bv ma = mg - bv t = m/b, which the time constant which is the ma = mg - bv amount of time required for the object to achieve As v increases, acceleration decreases. 63% of it's maximum speed...(ask during class if not clear). a = g - bv/m where a = dv / dt dv/dt = g - bv/m Integrate v = (mg/b) (1 - e-bt/m) v = (mg/b) (1 - e-t / t)