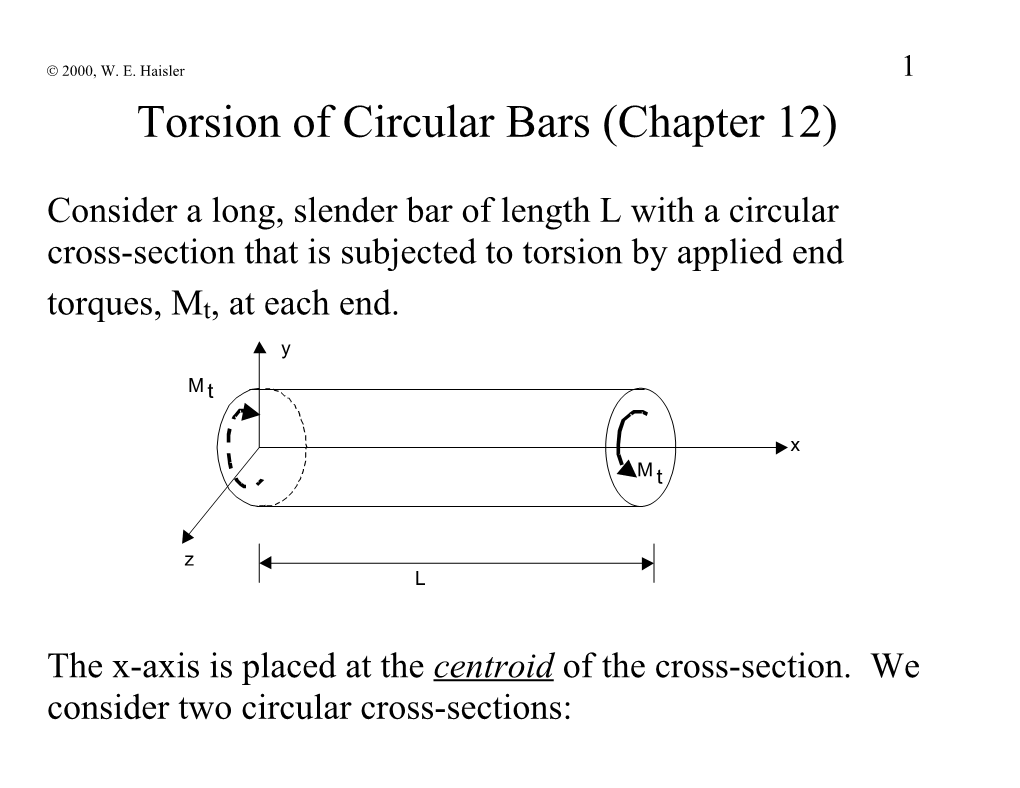
Chapter 11 - Stress, Strain and Deformation in Solids

 2000, W. E. Haisler 1 Torsion of Circular Bars (Chapter 12)

Consider a long, slender bar of length L with a circular cross-section that is subjected to torsion by applied end torques, Mt, at each end. y

The x-axis is placed at the centroid of the cross-section. We consider two circular cross-sections:  2000, W. E. Haisler 2 1) Solid 2) Tube y D o D i

The cross-section has an important geometrically property; the polar moment of inertia, J: J r2 dA  r 2 rdrd ( y 2  z 2 ) dydz  I  I A   zz yy 4 For a solid of diameter D, J   D . 32 Before developing a theory for how a bar twists and deforms under a torque loading, it is very instructive to experimentally observe the deformation pattern of a twisted  2000, W. E. Haisler 3 bar as shown in the following photograph. The undeformed bar has straight lines that run the length of bar as well as circular lines around the circumference.

Circular bar twisted by end torques  2000, W. E. Haisler 4 Note that these lines form a pattern of squares on the surface of the bar. After twisting (lower photograph), the straight lines spiral around the bar and the circular lines remain circles. For a small area on the curved surface (say one of the squares), the spiraling lines would be straight if the curved surface were laid out flat. Each square is now a parallelogram, which suggest that a shear (shear stress) has been applied to the square.

Kinematics So to begin the development of the theory, we scribe a line on the surface of the bar that runs the length of the bar from a to b. For convenience, we assume the left end of the bar is fixed from rotation. As the bar is twisted by a torque of Mt on the right, the line 0-a will rotate to position 0-a’.  2000, W. E. Haisler 5 Experimentally, it is observed for a circular cross-section that line 0-a remains a straight line as it is rotated to position 0-a’. Looking at the end cross-section where Mt is applied, we see the line b-a has rotated CCW to b-a’ by an angle . line 0a moves y y y uz a to 0a’ a u 0 a u y  M  t a’ Mt x a’ a’ r z z b x z x

Cartesian Polar (r- in y-z plane)  represents the angle of twist for the cross-section located at x (assuming the cross-section at x=0 was fixed).  2000, W. E. Haisler 6 Based on the physical observation discussed earlier, we postulate the following displacements (in Cartesian coords).  Since we saw no motion in the x direction, then ux  0.  For small angular rotations, we can relate the motion in the y-z plane, i.e., uy and uz, through geometry to the angle of twist  and write uy   z and uz   y.  uy These are obtained from the approximations: a’ z uz uy tan   and tan   . The negative a’ u y z z in uy is because uy is negative (down) for y  positive  .  These assumptions are reasonable if  is not too large. We note that the angle of twist is a function of x so that  (x ).  2000, W. E. Haisler 7 In polar coordinates, we assume ur  0 y u  0 a and x [no displacement in radial u and axial (x) direction]. These last two  assumptions are equivalent to saying a’ r z that the diameter of the bar does not x increase during twisting and the bar does not change length, which is consistent with experimental observation. Finally, from geometry the circumferential displacement of a point is proportional to the angle of twist  and it's radial position, r: u  r . Polar coordinates should be much easier to work with.

In order to determine the strain for these displacements, consider the experiment referred to above. If one rolls out  2000, W. E. Haisler 8 the curved surface of the bar into a flat surface, we have the following (for a length of the bar between x and x+x):

x x  x y x a a x u u   a’  a’ r  z  x



In the x-y plane, the angle  represents the change in right angle for one of the original squares and will define the  2000, W. E. Haisler 9 strain  x (or engineering shear strain,  x . We can write the following for the engineering shear strain:

u u   u   u  u   tan1 x x x  x  x x   x   x   x  x

But the displacement is given by :u  r so that

    r and 1   1 r . x x x2 x  2 x

Note that the above assumes that the bar is prismatic (r is a constant).  2000, W. E. Haisler 10 If we want to do this more precisely, we can use the tensor strain definitions in polar coordinates to obtain (recall that ur  0, ux  0, u  r ):

u u u1  u  r  0,  x  0,  r   0 rr r xx x  r r 

1u 1  ux  1    x     r , x 2  x   r 2x r   2  x x

1 1 ur  u u   r      0, 2 r  r r  1 ur  u x  rx     0 2 x  r   2000, W. E. Haisler 11 Constitutive Relation

For an elastic, isotropic material, we can write the stress- strain relation as

 E   Ex  E   G  x(1 ) x  (1   )2 2(1   ) x  x  where E G = shear modulus = 2(1 )  2000, W. E. Haisler 12 y Equilibrium dA=r drd

The torque Mt(x) on the cross-section at z location (x) must be in equilibrium with r the internal moment produced by the  x Mt z  x shear stress  x . M r dA tA x Now substitute the constitutive and cross-section at x kinematic relations into the equilibrium equation: d d  M r dA  G  dA  rG( r ) dA  G r2 dA tA x  A x   Adx  A dx Both G and the angle of twist are a constant for a given cross-section located at x so that we have:  2000, W. E. Haisler 13 d M G r2 dA. The integral is a geometrical property t dx A of the cross-section A called J, the polar moment of inertia, 2 so that J r dA and thus we have A d M JG t dx The above equilibrium equation can be integrated between two points on the bar, say x0 and xL to obtain: x M (x )  ( x )  L t dx L 0  JG x0 Note that Mt M t ( x ). You must know (x0 ) [as a boundary condition] to determine (xL )!!!  2000, W. E. Haisler 14 Example: Now consider a circular elastic bar with diameter D, length L, shear modulus G, and with applied torques Mt at each end. The left end is held fixed from rotation. Determine the rotation at the free end (x=L).

y =0 at left end (fixed) elastic bar, diameter = D M t M t

internal torque M t diagram x

z L x=L d We start with equilibrium: M JG . Integrate the ODE t dx from x=0 to x=L to obtain:  2000, W. E. Haisler 15 L Mt (L )  (0)   dx. 0 JG For this problem, the torque Mt is a constant along the length of the bar (and equal to the applied torque at each end). For a prismatic bar, J is also a constant. Hence we can write: M L 0 M L (L )  (0) t  dx   (0)  t JG 0 JG Since the boundary condition is that the bar is fixed at x=0, (0) 0. Letting L  (L ) M L   t L JG L is angle of twist for a bar of length L with a constant torque, Mt .  2000, W. E. Haisler 16 To determine stress, recall that the constitutive equation is x G  x  and the stress-strain equation is    r x x Hence the shear stress is d   Gr x dx But from the equilibrium equation we have d d M M JG or  t t dx dx JG Hence the shear stress becomes:

M r   t x J  2000, W. E. Haisler 17 Summary of important equations:

J r2 dA A d Mt    dx JG  x General equations when Mt M t ( x ) L Mt (xL )  ( x0 )   dx JG  x0  Mt L  L  Angle of twist for constant Mt at ends JG  M r   t x J  2000, W. E. Haisler 18 Example: A circular bar with diameter of 0.5 in, length of 50 in, and made of steel (G=11.5x106 psi) carries a torque of 30 ft-lb. D=0.5 in 30 ft-lb 30 ft-lb steel 50 in Determine the angle of twist of end relative to the other and the maximum shear stress. D4  (0.5 in ) 4 J r2 dA    0.00614 in 4 A 32 32 Mt L(30 x 12 in lb )(50 in ) L   0.255rad  14.6deg JG (.00614in4 )(11.5 x 10 6 psi ) Mt r(30 x 12 in lb )(0.25 in )  x   14,658psi J 0.00614in4  2000, W. E. Haisler 19

Distributed Torque. mt ( x ) Consider the torsion of circular bar with distributed torque of mt(x) applied Mt ( x ) mt ( x ) Mt ( x dx ) along it's length [units of torque/length]. For dx moment equilibrium: x x dx Mt( x dx )  M t ( x )  m t dx  0 Divide by dx and take the limit to obtain

 M t m  0  x t  2000, W. E. Haisler 20

The above can be integrated to obtain Mt(x). We can then substitute this Mt(x) into the differential equation for  and integrate from x1 to x2 to obtain (x2 ):

x2 (x2 )  ( x 1 )   ( Mt ( x )/ JG ) dx x1

You must know (x1 ) as a boundary condition.

d Alternately, we could substitute Mt  JG into dx  Mt d  mt  0 to obtain (JG ) mt  0. This last  x  x dx equation can be integrated twice to obtain . You obtain the same result either way.  2000, W. E. Haisler 21 Torsion of Circular Bars – Example Solutions

Example 1: The aluminum circular bar below has a constant diameter of 0.5 in. and a shear modulus of 4 million psi. Determine the 1) angle of twist at points B and C and 2) max shear stress in section AB and BC.

40 in-lb 75 in-lb

A x B C

20 in 35 in a) First, determine the internal torque (Mt) as a function of x.  2000, W. E. Haisler 22 Since torque is applied only at point B and C, the internal torque will be constant between A and B and between B and C. Assume the internal torque in section A-B is Mt1 and in B-C is Mt2 (note: assume Mt is positive).

M M M M t 1 t 1 t 2 t 2 1 2

A B B C Make cuts between A and B and between B and C, and draw free-body diagrams as below:

40 in-lb 75 in-lb M M A t 1 B t 2 C

free-body 1 free-body 2  2000, W. E. Haisler 23 Starting with the free-body 2, we write moment (torque) equilibrium equations: free body#2 :  M  0  75  Mt2  M t 2  75 in-lb free body#1:  M  0  Mt2  40  M t 1  M t 1  M t 2  40  75 40  35 in-lb This structure is STATICALLY DETERMINANT since we could find all internal torques by equilibrium alone. The torque diagram can now be drawn: M t 75 in-lb 35

x 0 20 55 in.  2000, W. E. Haisler 24 b) Determine the twist of each section. 35 35 75 75 1 2 A B B C

4  (0.5)4 J J  D   0.00613 in4 1 2 32 32 Mt1 L 1 35(20) twist of bar 1: 1    0.0285rad J1 G 1 0.00613(4x 106 ) M L 75(35)  t2 2   0.107rad twist of bar 2: 2 6 J2 G 2 0.00613(4x 10 )

A = rotation at A = 0 (boundary condition)

B = rotation at A + twist of bar 1 = A + 1 = 0 + 0.0285 = 0.0285 rad = 1.63 deg  2000, W. E. Haisler 25

C = rotation at B + twist of bar 2 = B + 2 = 0.0285 + 0.107 = 0.136 rad = 7.77 deg

An alternate method for part b is to integrate the torque diagrams: B Mt 20" 35 20 B  A dx 0  dx  (0.00143) x A JG 0" 0.00613(4x 106 ) 0  0.0285rad  1.64deg C Mt 55" 75 C  B dx 0.0285 rad  dx B JG 20" 0.00613(4x 106 ) 0.0285 0.0031x 55 0.0285 0.107  20    0.136rad  7.77deg  2000, W. E. Haisler 26 c) Determine the maximum stress in each section

M r 35in lb (0.5/ 2 in )  t1 1  1,427 psi x1 4 J1 0.00613in

Mt2 r 2 75(0.5/ 2)  x 2    3,059 psi J2 0.00613  2000, W. E. Haisler 27 Example 2: Consider the following aluminum bar in torsion. The diameters of sections AB, BC and CD are 0.5 in, 0.75 in and 0.5 in, respectively. The shear modulus for aluminum is 4 million psi. A B C D 1 2 3 40 in-lb 75 in-lb

20 in 30 in 20 in a) The internal torques in each of the bars are labeled Mt1, Mt2, and Mt3 (from left to right). Make cuts in each bar and isolate the free-bodies. Now use equilibrium to relate the internal torques.  2000, W. E. Haisler 28

M t 40 in-lb M t 75 in-lb M A 1 B 2 C t 3 D free-body 1 free-body 2 free body#1:  M  0  Mt2  40  M t 1

free body#2 :  M  0  Mt3  75  M t 2

Note that this structure is STATICALLY INDETERMINATE since we CANNOT find all internal torques by equilibrium alone.

b) Determine J and angle of twist of each bar.  2000, W. E. Haisler 29

4  (.5)4 J J  D   0.0061 in4 1 3 32 32 4  (.75)4 J D   0.031 in4 2 32 32 M L M (20)  t1 1  t 1  0.00082M 16 t 1 J1 G 1 0.0061(4x 10 ) M L M (30)  t2 2  t 2  0.000242M 26 t 2 J2 G 2 0.031(4x 10 ) M L M (20)  t3 3  t 3  0.00082M 36 t 3 J3 G 3 0.0061(4x 10 )  2000, W. E. Haisler 30 c) Apply the boundary condition. Since the bar is fixed between two rigid walls, the total twist must be zero.

total angle of twist 0 1   2   3

0 0.00082Mt1  0.000242 M t 2  0.00082 M t 3  2000, W. E. Haisler 31 d) Now combine the two equilibrium equations and the one boundary condition equation.

Mt1  M t 2  40 Mt2  M t 3  75 0.00082Mt1 0.000242 M t 2  0.00082 M t 3  0 or in matrix notation,

1 1 0  Mt1   40 in  lb      0 1 1  M   75 in  lb   t2        0.00082 0.000242 0.00082  Mt3   0 

Solving for the unknown torques, one obtains using Maple  2000, W. E. Haisler 32 > with (linalg): > A := array([[-1,1,0],[0,-1,1] ,[0.00082,0.000242,0.00082]]); [ -1 1 0 ] [ ] A := [ 0 -1 1 ] [ ] [.00082 .000242 .00082] > b := array([40,-75,0]); b := [40, -75, 0] > linsolve(A,b); [10.10626992, 50.10626992, -24.89373008]  2000, W. E. Haisler 33 Thus, Mt110.11 in  lb , M t 1  50.11 in  lb , M t 3   24.9 in  lb e) We can now solve for the individual angles of twist or the shear stress. For example,

Rotation of point A1  0.00082Mt 1  0.00082(10.11)  0.00829rad  0.47deg

Rotation of point B1   2  0.00829rad  0.000242 Mt 2  0.00829  0.000242(50.11)  0.0204rad  1.17deg  2000, W. E. Haisler 34 Stress in bar 1: M r 10.11in lb (0.5 in / 2)  t1 1   414 psi x1 4 J1 0.0061in

Stress in bar 2: Mt2 r 2 50.11(0.75/ 2)  x 2    606 psi J2 0.031  2000, W. E. Haisler 35 Example 3: Bar with distributed torque of 60 in-lb/in applied from A to B and a concentrated torque of 400 in-lb at C. Material is steel with a shear modulus of 11.5 million psi. Bars are cylindrical with diameters of 0.4 in (A-B) and 0.25 in (B-C). 60 in-lb/in 1 400 in-lb A x B C

5 in 8 in a) First construct the distributed torque diagram (mt vs x)  2000, W. E. Haisler 36 m t 5 13 in. x 0

-60 in-lb/in b) Now construct the internal torque diagram by using  M integration of t  m  x t At x=13", Mt (13 in ) 400 in  lb For 5x  13", x x Mt( x ) M t (13) 13 m t dx  400   13 (  60) dx  400  60( x  13) At x=5" (from equation above), Mt (5)  80 in  lb For 0x  5",  2000, W. E. Haisler 37 x x Mt( x ) M t (5) 5 m t dx   80   5 (0) dx   80 in  lb

Now construct the internal torque diagram for the strucuture. M t 400+60(x-13) 400 in-lb

5 in. x 13 in. -80 in-lb c) Now determine the angle of twist using integration of the internal torque. First obtain the polar moment of inertia for section:  2000, W. E. Haisler 38 4  (.4)4 J D   0.00251 in4 1 32 32 4  (.25)4 J D   0.000383 in4 2 32 32 for 0x  5", xM x ( 80) (x )  (0) t dx  0  dx   0.0029 x 6 0J1 G 1  0 (0.00251)(11x 10 )  (5") = -0.0029(5) = -0.0145 rad -= - 0.83 deg

for 5x  13",  2000, W. E. Haisler 39 xM x [400 60(x  13)] (x )  (5) t dx   .0145  dx 5J2 G 2  5 J 2 G 2 x   .0145 1 (  380x  30 x2 ) .000383(11x 106 ) 5   0.0145 1 [  380x  30 x2  1,150] 4,213

Evaluate the above at x=13":

 (13") = -0.0145 + 0.304 = 0.289 rad = 16.6 deg  2000, W. E. Haisler 40 d) Now determine stresses at various x points. Be sure to

use Mt, r and J for desired x value (get Mt from torque diagram).

At x = 5 in, M( x 5) r 80in  lb (0.4"/ 2)  (x 5") t    6,375 psi x 4 J1 0.00251in At x = 9 in, (get Mt from torque diagram) M( x 9") r 160 in lb (0.25"/ 2)  (x 9") t   52,219 psi x 4 J2 0.000383 in At x = 13 in, M( x 13) r 400 in lb (0.25"/ 2)  (x 13") t   130,550 psi x 4 J2 0.000383 in  2000, W. E. Haisler 41 Note: depending upon the type of steel, the material may fail before reaching a shear stress of 130 ksi.

If the stress in section BC is too high, must increase the diameter of section BC (new J2), and repeat calculations for angles of twist and stress in section BC. Section AB calculations would be unaffected since J1 was not changed.