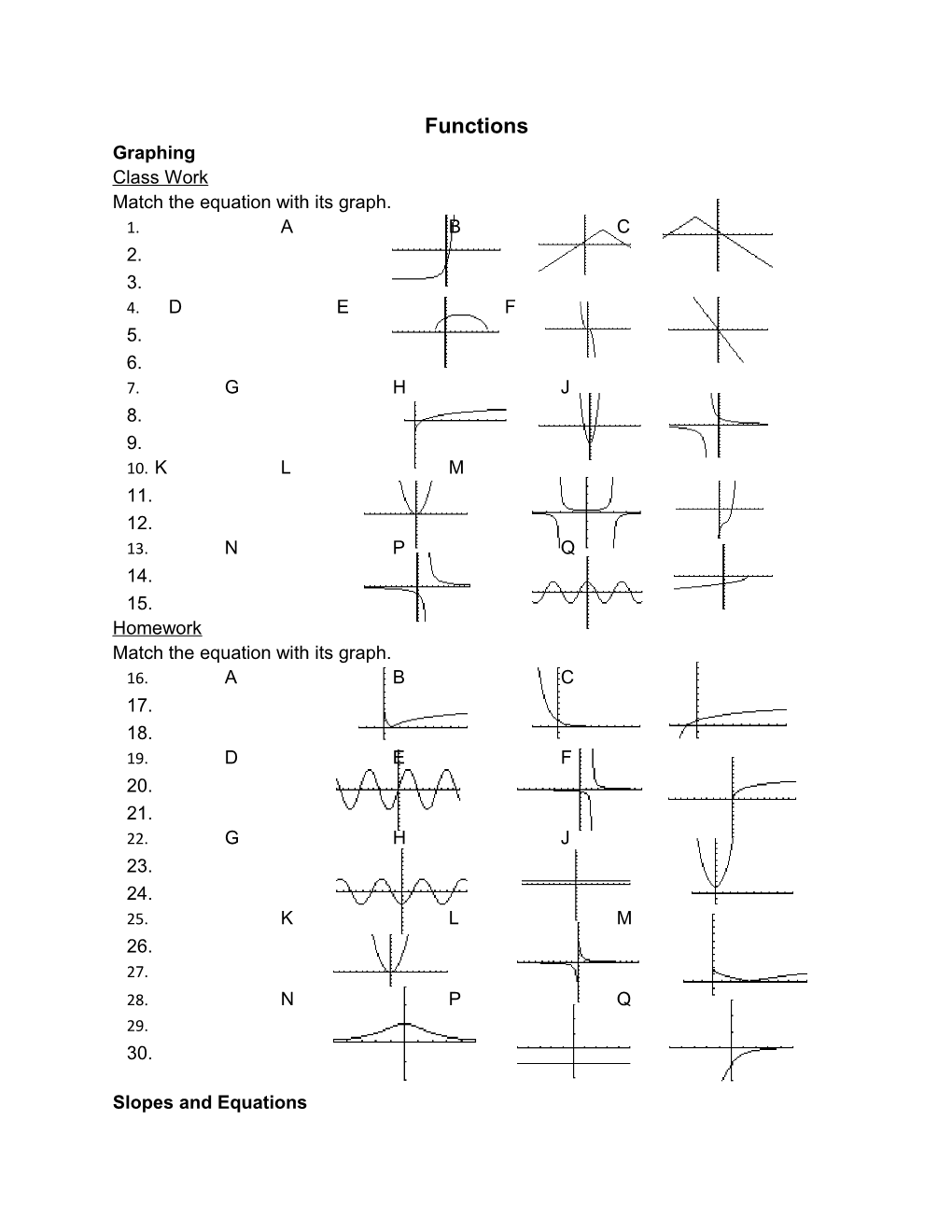
Functions Graphing Class Work Match the equation with its graph. 1. A B C 2. 3. 4. D E F 5. 6. 7. G H J 8. 9. 10. K L M 11. 12. 13. N P Q 14. 15. Homework Match the equation with its graph. 16. A B C 17. 18. 19. D E F 20. 21. 22. G H J 23. 24. 25. K L M 26. 27. 28. N P Q 29. 30.
Slopes and Equations Class Work 31. What is the slope of the line through M(2, -3) and N(4, -1)? 32. Write the equation of the line through M(2, -3) and N(4, -1) in slope-intercept form. 33. Write the equation of the line through M(2, -3) and N(4, -1) in point-slope form. 34. Write the equation of the line through M(2, -3) and N(4, -1) in standard form. 35. Write the equation of the line through (4, 5) and parallel to y -6=2(x+5). 36. Write the equation of the line through (4, 5) and perpendicular to y -6=2(x+5). 37. 3x - y=5 and y - 6 = a(x+6) are perpendicular, find a. 38. Use the table at the right to answer the following:
110 a. Write a prediction equation for the data. 105 100 b. What does slope mean in your equation? 95
s 90 e r o
c 85 s
c. Predict what grade comes from studying t
s 80 e t 75 45 minutes? 70 65 d. How long would you need to study for a 100? 60 25 30 35 40 45 50 55 60 Tim e s pe nt s tudying Homework 39. What is the slope of the line through M(5,0) and N(4, -6)? 40. Write the equation of the line through M(5,0) and N(4, -6) in slope-intercept form. 41. Write the equation of the line through M(5,0) and N(4, -6) in point-slope form. 42. Write the equation of the line through M(5,0) and N(4, -6) in standard form. 43. Write the equation of the line through (8,2) and parallel to y - 7=3(x - 5). 44. Write the equation of the line through (4, 5) and perpendicular to y - 7=3(x - 5). 45. 4x - 2y=5 and 2x + ay = 7 are perpendicular, find a. Use the table at the right to answer the following: 46. 11:55
a. Write a prediction equation for the data. 10:43 What does slope mean in your equation? b. e 9:31 m i t
e l i
c. Predict what time comes from training M 8:19
6 hours? 7:07
d. How long would you need to train to be 5:55 0 5 10 15 20 25 7 minutes? Time spent training
Relations, Functions, and Their Graphs Class Work State the domain and range for the following. Find when f(x)=0. Graph the function. 47. 48. 49. 50. 51. Is the following function an odd-function, an even-function or neither. 52. 53. 54. 55. 56. Use the piecewise function at right to answer the following: a. f(-2) b. f(0) c. f(4) d. state the domain and range of f e. graph f 57. Use the piecewise function at right to answer the following: a. f(-2) b. f(2) c. f(4) d. state the domain and range of f e. graph f 58. Write a piecewise function for the graph.
Homework State the domain and range for the following. Find when f(x)=0. Graph the function. 59. 60. 61. 62. 63. Is the following function an odd-function, an even-function or neither. 64. 65. 66. 67. 68. Use the piecewise function to answer the following. a. f(-2) b. f(1) c. f(4) d. state the domain and range of f e. graph f 69. Use the piecewise function to answer the following. a. f(-2) b. f(2) c. f(4) d. state the domain and range of f e. graph 70. Write a piecewise function for the graph.
Exponential Functions Class Work Graph the following functions. State the domain and range for each. Find any zeros. 71. 72. 73. 74. 75. 76. Write equations for the following graphs. (Each has base e.) Window is [-5,5] by [-5,5] A. B. C.
77. $250 is deposited in an account earning 5% that compounds quarterly, what is the balance in the account after 3 years? 78. A bacteria colony is growing at a continuous rate of 3% per day. If there were 5 grams to start, what is the mass of the colony in 10 days? 79. A bacteria colony is growing at a continuous rate of 4% per day. How long till the colony doubles in size? 80. If a car depreciates at an annual rate of 12% and you paid $30,000 for it, how much is it worth in 5 years? 81. An unknown isotope is measured to have 250 grams at start and 175 grams on day 30. At what rate is the isotope decaying? At what point will there be 100 grams left? 82. An antique watch made in 1752 was worth $180 in 1950; in 2000 it was worth $2200. If the watch’s value is appreciating continuously, what would its value be in 2010? 83. A furniture store sells a $3000 living room and doesn’t require payment for 2 years. If interest is charged at a 5% continuous rate and no money is paid early, how much money is repaid at the end? Homework Graph the following functions. State the domain and range for each. Find any zeros. 84. 85. 86. 87. 88. 89. Write an equation for the following graphs. (Each has base e.) Window is [-5,5] by [-5,5] A. B. C.
90. $50 is deposited in an account that earns 4% compounds monthly, what is the balance in the account after 4 years? 91. A bacteria colony is growing at a continuous rate of 5% per day. If there were 7 grams to start, what is the mass of the colony in 20 days? 92. A bacteria colony is growing at a continuous rate of 6% per day. How long till the colony doubles in size? 93. If a car depreciates at an annual rate of 10% and you paid $20,000 for it, how much is it worth in 4 years? 94. An unknown isotope is measured to have 200 grams at the start and 150 grams on day 30. At what rate is the isotope decaying? At what point will there be 50 grams left? 95. An antique watch made in 1752 was worth $280 in 1940; in 2000 it was worth $3200. If the watch’s value is appreciating continuously, what would its value be in 2010? 96. A $9000 credit card bill isn’t paid one month, the credit company charges .5% continuously on unpaid amounts. How much is owed 30 days later? (assume no other charges are made) Transformations Class Work In each exercise the function h(x) is given. (i) Identify its parent function, (ii) describe the transformation(s) needed to go from the parent function to h(x), (iii) determine the domain and range, and (iv) draw the graph of both. 97. 98. 99. 100. 101. The graph at right is the graph of f(x). Draw the graphs of the h(x). 102. 103. 104. 105.
Homework In each exercise the function h(x) is given. (i) Identify its parent function, (ii) describe the transformation(s) needed to go from the parent function to h(x), (iii) determine the domain and range, and (iv) draw the graph of both. 106. 107. 108. 109. 110. The graph at right is the graph of f(x). Draw the graphs of h(x). 111. 112. 113. 114.
Solving Equations and Inequalities Class Work Solve algebraically. 115. 116. 117. 118. 119. 120. Solve graphically. 121. 122. 123. A farmer wants to make 2 pens with 800 ft of fencing. The pens will share a common side. What are the dimensions of one pen that maximize the fence? 124. A gardener wants to pen in a garden using her house as one side. The garden is to be 200 sq ft. How much fence is needed if the gardener is trying to minimize the fence? 125. An open top box is formed by cutting the same size square out of each corner of a rectangular piece of material. If the sheet is 8m by 10m. What is the maximum volume possible? 126. A pizza box is created by cutting 6 equal squares out of the corners and the middles of the two longest sides of a 20” by 50” piece of cardboard. What is the largest diameter pizza when the box is maximized for volume? Homework Solve algebraically. 127. 128. 129. 130. 131. 132. Solve graphically. 133. 134. 135. A farmer wants to make 2 pens with 600 ft of fencing. The pens will share a common side. What are the dimensions of one pen that maximize the fence? 136. A gardener wants to pen in a garden using 10’ of her house as part of one side. The garden is to be 400 sq ft. How much fence is needed if the gardener is trying to minimize the fence? 137. An open top box is formed by cutting the same size square out of each corner of a rectangular piece of material. If the sheet is 14m by 8m. What is the maximum volume possible? 138. A pizza box is created by cutting 6 equal squares out of the corners and the middles of the two longest sides of a 30” by 70” piece of cardboard. What is the largest diameter pizza when the box is maximized for volume?
Relations, Functions, and Their Inverses Class Work Given f(x), find f-1(x). Show that f(f-1(x)) = f-1(f(x)) = x. Graph f(x) and f-1(x) on the same graph. Describe the domain and range for f -1(x). 139. 140. 141. 142. 143. 144. 145.
Homework Given f(x), find f-1(x). Show that f(f-1(x)) = f-1(f(x)) = x. Graph f(x) and f-1(x) on the same graph. Describe the domain and range for f -1(x). 146. 147. 148. 149. 150. 151. 152. Trig Class Work Find the exact value of the given expression. 153. 154. 155. 156. 157. 158. 159. Given the terminal point 160. Given the terminal point 161. Knowing cosx=and the terminal point is in the fourth quadrant find sinx. 162. Knowing cotx=and the terminal point is in the third quadrant find secx. State the amplitude, period, phase shift, and vertical shift for each function. Draw the graph by hand and then check it with a graphing calculator. 163. 164. 165. 166. 167. Evaluate the expression. 168. 169. 170. 171. 172. Homework Find the exact value of the given expression. 173. 174. 175. 176. 177. 178. 179. Given the terminal point 180. Given the terminal point 181. Knowing sinx=and the terminal point is in the second quadrant find secx. 182. Knowing cscx=and the terminal point is in the third quadrant find cotx. State the amplitude, period, phase shift, and vertical shift for each function. Draw the graph by hand and then check it with a graphing calculator. 183. 184. 185. 186. 187. Evaluate the expression. 188. 189. 190. 191. 192.
Parametric Equations Class Work 193. A t-shirt cannon launches a shirt at initial vertical velocity of 30ft/sec and a horizontal velocity of 20 ft/sec. The cannon is 5 ft off the ground at the time of launch. a. write a parametric equation to model this situation b. when is the t-shirt 15 ft above the ground? c. the person launching the shirt gets a shirt to a patron 10’ off the ground on the downward arc. How long did the shirt stay in the air? d. Considering part C, how far did the shirt travel horizontally?
194. Cal C. notices a ladybug on the window of his math classroom, considers the window to be the first quadrant, and writes a parametric equation the bug’s motion: x= 3t + 20 y=-4t + 30 a. what does each part of the equation represent? b. what direction is the bug traveling? c. If the window is 50 by 80, when does the bug reach a side and which side?
Homework
195. A t-shirt cannon launches a shirt at initial vertical velocity of 40ft/sec and a horizontal velocity of 25 ft/sec. The cannon is 4 ft off the ground at the time of launch. a. write a parametric equation to model this situation b. when is the t-shirt 20 ft above the ground? c. the person launching the shirt gets a shirt to a patron 28’ off the ground on the downward arc. How long did the shirt stay in the air? d. Considering part C, how far did the shirt travel horizontally?
196. Cal C. notices a ladybug on the window of his math classroom, considers the window to be the first quadrant, and writes a parametric equation the bug’s motion: x= -2t + 25 y= 3t + 50 a. what does each part of the equation represent? b. what direction is the bug traveling? c. If the window is 50 by 80, when does the bug reach a side and which side?
Multiple Choice Without a Calculator 1. Which of the following is undefined at x=2? a. b. c. d. e. 2. What is the equation of the line through (2,6) and perpendicular to 2x +3y=7? a. b. c. d. e. 3. Which of the following graphs is symmetric to the origin? a. b. c. d. e. 4. If and find h(x) if h(x)= a. b. c. d. e. 5. The function has the maximum value of a. -2 b. c. d. 2 e. 3 6. The zero for is between a. -2 and -1 b. -1 and 0 c. 0 and 1 d. 1 and 2 e. 2 and 3 Calculator Permitted 7. The prediction equation of C(x)= .2x + 4 for a taxi ride where C is the cost and x is in tenths of a mile. What is the predict cost of a 3 mile ride? a. $4.23 b. $4.60 c. $6 d. $10 8. Which of the following equations is symmetric to the y-axis? a. b. c. d. 9. The function has how many zero(s)? a. 0 b. 1 c. 2 d. 3 e. 4 10. The inverse of is a. b. c. d. e. 11. a. b. c. d. e. 12. If f(x) is an odd function, which of the following must be true? a. f(x) = f(-x) b. f(x) = -f(x) c. f(-x) = -f(x) d. f-1(x) = f(x) e. f-1(x) = f(-x) In questions 13 and 14, consider the following parametric: 13. The initial vertical velocity is a. 4 b. 7 c. 8 d. -2 e. -9
14. The position at t=3 is approximately how far from the initial position? a. 12 b. 24 c. 27 d. 36 e. 44
Open Ended Without a Calculator 1. Let , a. find the rate of change from x=3 to x=6 b. find the rate of change from x=4 to x=4.1 c. find the rate of change from x to x+h 2. Given the graphs of f(x)= and g(x)= find a. f(g(0)) b. g(f(-1)) c. f-1(1) d. For what value of x is g(f(x)) a maximum? 3. a. show that b. graph f(x) and f-1(x) c. find f(ln 4) Calculator Permitted 4. Solve the equation a. Solve b. Solve c. How is the solution to the original equation related to the solution of the inequalities? 5. Given the function a. when is the function increasing? decreasing? b. when is the function at a maximum? minimum? c. How are the answers to parts a and b related? 6. An arrow is shot at a target with an initial vertical velocity 20’/sec and horizontal velocity of 30’/sec. The archer was standing at a line 75’ from the target, and the bow 4’ off the ground and 2’ in front of the line. a. Write a parametric equation to model this situation. b. Where is the arrow 1 sec after launch? c. If the target has a 4’ diameter and is 2’ off the ground, does the arrow hit the target (exclude left and right of the target.)
Answer Key 1. G 21. J
2. H 22. D
3. J 23. H
4. D 24. E
5. E 25. L
6. F 26. G
7. A 27. K
8. C 28. N
9. B 29. P
10. M 30. Q
11. L 31. 1
12. : 32. Y=x-5
13. Q 33. Y+3=(x-2)
14. N 34. X-y=5
15. P 35. Y-5=2(x-4)
16. F 36. Y-5=-1/2(x-4)
17. C 37. -1/3
18. A 38. A) G=9/10(t-50) +90; b) for every ten minutes more studying, grade goes up 19. M nine points; C)85.5; D)135 minutes
20. B 39. 6 40. Y=6x-5 60. D: reals; R: [-4,∞) f(0) =-2
41. Y-4=6(x+6) 61. D: x≠ 0; R: f(x)≠2; f(0)= undefined
42. 6x-y=5 62. D: x≠1: R: f(x) ≠0; f(0) =2
43. Y-2=3(x-8) 63. D: 0,∞) R: reals f(0) = undefined
44. Y-5=-1/3(x-4) 64. Even
45. 4 65. Neither
46. A) y-8.55=-3/17(x-3); B)17 hours more in 66. Neither training you get three minutes dropped in time; C) 8:23.235 minutes; D) 10 hrs 67. Odd 54,667 minutes 68. A) 1; B)2; C) 2; D) D:reals, R:[2,
47. D: [-4/3, ∞) R: [13, ∞) f(0)=15 69. A) 4; B) 2; C) 4 D) D: reals R: [0, ∞)
48. D: reals R: [4, ∞) f(0)=6 70. Y = -x-1 if x<-1 49. D: x≠2; R: f(x)≠1/5 f(0)= -1/5 X+1 if -1≤x<1 50. D: x≠1: R: f(x)≠0 f(0)=4 2 if x ≥1 51. D: reals R=(0,∞) f(0)=1/2 71. D: reals R: (-6,∞) Zeroes 6 52. Neither 72. D: reals R: (-∞,0) Zeros: none 53. Odd 73. D: reals R: (-∞,6) Zeros: ln 2 54. Odd 74. D: reals R: (0, ∞) Zeros: none 55. Even 75. D: reals R(-1, ∞) Zeros: (ln1) (ln2) 56. A) -5; B) 0; C)4; D) Domain: reals R: (-∞, 76. A) y=3ex-2 B) y= 3-2e-x C) y=3ex -1) U (0,∞) 77. $290.19 57. A) -2; B)-2; C) -4; D) Domain: reals R= (- ∞, -2) 78. 8.244 grams
58. F(x)= 2x-1 x<0 79. 17.329 days
3 0≤x <3 80. $15,832
-1x x≥3 81. K= -.017; 77.069 days
59. D: (-∞, 2.5] R: [7,∞) f(0)= 7+ 82. $3629.55 83. $3315.99 104. Graph
84. D: reals R: (2, ∞) zeros: none 105. Graph
85. D: Reals R: (-2, ∞) zeros: -ln 2 106. Y= x 1/3; horizontal shrink ½; 3/2 right; vertical stretch of 4; up 2; D: reals R: 86. D: reals R: (-∞,5) zeros: ln 2.5 reals
87. D: reals R: (-∞,0) xeros: none 107. Y= ; right 2; vertical stretch 3; up 4; D: 88. D: reals R: (-2, ∞) zeros: (ln2)/ln3 x≠0 ; R: (-4, ∞)
89. A) y=-2+e-x B) y=4-e-x C) y=1+ex 108. Y=cosx; horizointal shrink ½; right; vert stretch 2; down 3; D: reals; R: [-5, -1] 90. $58.66 109. Y=tanx; reflect over y-axis; horizontal 91. 19.028 grams stretch of 2; reflect over x-axis; up 1: D: x +kn; R: reals 92. 11.553 days 110. Reflect over y-axis; 2 right; up 4; D: x<2: 93. $13,122 R: Reals 94. R=-.009589; 144.565 days after start 111. Graph 95. $4802.66 112. Graph 96. $10,456.50 113. Graph 97. Y=x2; reflect over y axis, 3 left, vertical 114. Graph stretch of 4, D: reals R: [6, ∞) 115. 2 and 4 98. Y=1/x; horizontal shrink of ½; ½ left/ vertical stretch 3; down 2; D: x≠-1/2; R: 116. h(x) ≠-2 117. 99. Y=; reflect over y axis; 3 right; vertical stretch of 2; up 4; D: x≤3 R: [4, ∞) 118.
100. Horizontal shrink of 3; right 2; vertical 119. 8 and -2 stretch of 2; down 1; D: reals; R: [-1, ∞) 120. X<1 or x>7 101. Y=ex; reflect over y axis; horizontal shrink of ½; vertical stretch of 3; up 4; D: 121. 1.105 or 4.307 reals; R: (4, ∞) 122. x≤0 or x≥ 1.854
102. Graph 123. 133.3 feet by 100.00 feet
103. Graph 124. 10 feet by 20 feet 125. 52.514 m3 150. F-1(x)= e(x-1/2)
126. 11.909” 151. F-1(x) = e x+9
127. 10 and -2 152. F-1(x) = 3e X+8
128. 153. -1/2
129. 0 and +/- 154.
130. 4>y>-1 155. 2
131. -8 and 0 156.
132. X<-6 or x>9 157. -1
133. None 158. -1
134. -.820 and 3.524 159.
135. 100’ by 150’ 160. 136. 70 feet 161. 137. 82.981 m3 162. 138. 18.098’ 163. Ampl: 2; Period: ; vert shift: 1 139. F-1(x) = 164. Ampl: 3; Period: ; phase shift: 140. F-1(x) = +/- 165. Ampl: 1; Period: 3π; phase shift: ; vert 141. F-1(x) = +/- shift: 3
142. F-1(x) = 166. Ampl: 1; Period: ; phase shift: vert shift: -1 143. F-1(x) = ex-4 167. Ampl: 2/3; period ; phase shift: ; vert -1 144. F (x) = shift: 2
-1 x+6 145. F (x) =1/4 e 168. 12/3
-1 146. F (x) = 169. 147. F-1(x) = +/- 170. 148. F-1(x)= (x/9)e/2 171. 149. F-1(x) = +/- 172. 173. ½ c)1.69sec d)33.8ft 174. 194. a)3 hor. vel, 20 hor. dist from origin, -4 vert. vel, 30 vert. dist from origin. b) right and down c) bottom, 7.5 sec 175. -2 195. x(t)=25t y(t)=-16t2 + 40t + 4 176. b).5 & 2 sec c) 1.5 sec 177. 1 d) 37.5’ 196. a)-2 hor. vel, 25 hor. dist from origin, 3 178. 1 vert. vel, 50 vert. dist from origin b) left and up 179. -7/24 c) top side, 10 sec
180.
181. MULTIPLE CHOICE:
182. ¾ 1. E
183. Ampl: 4; Period: 4π; phase shift: ; vert 2. C shift: 2 3. D
184. Ampl: 2; Period: ; Phase shift: ; vert 4. D shift: -3 5. E 185. Ampl: 2; Period: 8π; phase shift: ; vert shift: 1 6. D
186. Ampl: 1; period: ; phase shift: ; vert 7. D shift: -1 8. B 187. Ampl: 3/2; period: π; phase shift: ; vert 9. D shift: -2 10. D 188. 5/13 11. C 189. 12. C 190. 13. C 191. 14. C 192. OPEN ENDED 193. a) x(t)=20t y(t)=-16t2+30t+5 1. A) 9; B) 8.1 C) 2x+h b)1.441 & .434 sec 2. A) -1 B) 0 C) 48 D) -3 or -1/2 Decreasing then increasing min 3. A) x=3e24, x/3 = e2y, ln x/3 = 2y, ½ ln (x/3) =y C) 48 6. A)
4. A) -2.426 B) x≥ -2.426 C) the B) 32 ft down the field, 8 ft off solution to the equation is the the ground endpoints for the inequalities C) No, the arrow only makes it 45 ft down the field before it 5. A) inc: (-∞, -1) U (1,∞) Dec: (- hits the ground 1,1) B) x=-1 x=1 C) increasing then decreasing max;