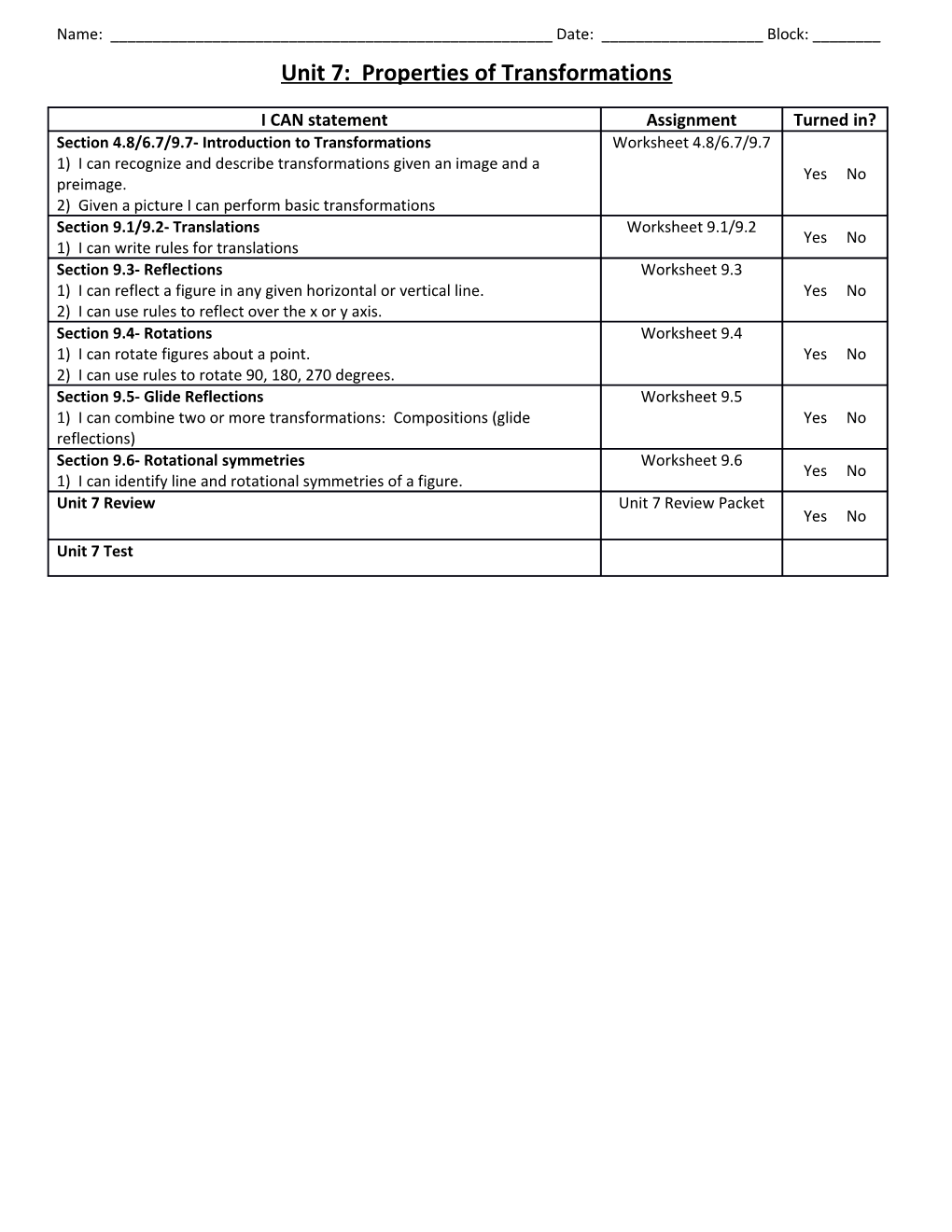
Unit 7: Properties of Transformations

Name: ______Date: ______Block: ______Unit 7: Properties of Transformations

I CAN statement Assignment Turned in? Section 4.8/6.7/9.7- Introduction to Transformations Worksheet 4.8/6.7/9.7 1) I can recognize and describe transformations given an image and a Yes No preimage. 2) Given a picture I can perform basic transformations Section 9.1/9.2- Translations Worksheet 9.1/9.2 Yes No 1) I can write rules for translations Section 9.3- Reflections Worksheet 9.3 1) I can reflect a figure in any given horizontal or vertical line. Yes No 2) I can use rules to reflect over the x or y axis. Section 9.4- Rotations Worksheet 9.4 1) I can rotate figures about a point. Yes No 2) I can use rules to rotate 90, 180, 270 degrees. Section 9.5- Glide Reflections Worksheet 9.5 1) I can combine two or more transformations: Compositions (glide Yes No reflections) Section 9.6- Rotational symmetries Worksheet 9.6 Yes No 1) I can identify line and rotational symmetries of a figure. Unit 7 Review Unit 7 Review Packet Yes No

Unit 7 Test Name: ______Date: ______Block: ______4.8/6.7/9.7- Introduction to Transformations Objectives: 1) I can recognize and describe transformations given an image and a preimage. 2) Given a picture I can perform basic transformations

Transformations

Preimage Image

Translation Rotation

Reflection Dilation

Example 1: Name the type of transformation depicted in the diagram below. Dashed figure (preimage)solid figure( image)

______

Example 2: Complete the statement using the description of the translation. In the description, points and are two vertices of a triangle. a) If translates to , then translates to ______.

b) If translates to , then translates to ______.

Example 3: A point on an image and the transformation are given. Find the corresponding point on the original figure. a) Point on the image: ; Transformation: ; Original point: ______

b) Point on the image: ; Transformation: ; Original point: ______

Example 4: Name: ______Date: ______Block: ______

Example 5: Use a reflection in the y-axis to draw the other half of the figure.

Scale Factor Name: ______Date: ______Block: ______

Example 6: State whether a dilation using the scale factor k results in a reduction or an enlargement.

a) b) c) d)

Example 7: Determine whether the dilation from Figure A to Figure B is a reduction or an enlargement. Find the scale factor. Then, find the values of the variables. a) b)

c) d) Name: ______Date: ______Block: ______9.1/9.2- Translations Objectives: 1) I can translate objects using a coordinate rule.

Translations

Example 1: Use the translation (x, y) --> (x-5, y + 8). 1. What is the image of ? 2. What is the image of ?

3. What is the preimage of? 4. What is the preimage of ?

5. What is the image of? 6. What is the preimage of ?

Example 2: Use the diagram to list the points that represent the polygon. a) b)

c) Quadrilateral ACDE d) Pentagon ABCDE

Example 3: Practice writing translation rules. Given the preimage: Write the image using the translation rule: a) b) c)

Example 6 : Translate 3 units left and 2 units down. Name: ______Date: ______Block: ______1) Rule?

Pre image: Image:

Translate: 5 units right and 6 units up. Translate: 7 units left and 9 units down. Name: ______Date: ______Block: ______9.3-Reflections in the Plane Objectives: 1) I can reflect a figure in any given horizontal or vertical line. 2) I can use coordinate rules to reflect over the x or y axis.

Definitions: Reflection

Reflection over the x-axis

Reflection over the y-axis

Example 1: Graph the reflection over the given line. Name: ______Date: ______Block: ______

Reflections Over the x-axis Over the y-axis

Example: Use the rules to find the image. Graph the polygon AND its image. a) Reflect in the x-axis

b) Reflect in the y-axis Name: ______Date: ______Block: ______9.4- Rotations in the Plane Objectives: 1) I can rotate figures about a point. 2) I can use coordinate to rotate 90, 180, 270 degrees.

Rotation

Example 1: Match the diagram with the angle of rotation.

Example 2: A rotation is an isometric transformation. Find the value of x, y, and z in the rotation of the triangle about P.

Rotation of Rotation of

Rotation of Rotation of Name: ______Date: ______Block: ______Example 3: Find the image that represents the rotation of the polygon about the origin. Then graph the polygon and its image. a) Rotate b) Rotate Name: ______Date: ______Block: ______9.5- Compositions Objectives: 1) I can combine two or more transformations (glide reflections)

Definitions: Composition

Glide reflection

Example 1: Describe the following compositions. a) b)

c) d) Name: ______Date: ______Block: ______Example 2: The endpoints of CD are C(1, 2) and D(5, 4). Graph the image of CD after the glide reflection. Name: ______Date: ______Block: ______9.6- Symmetry Objectives: 1) I can identify line and rotational symmetries of a figure.

Definition: Symmetry

Line symmetry

Rotational Symmetry

Example 1: Determine whether the figure has rotational symmetry. If so, describe the rotation that maps the figure onto itself.

Example 2: Use the description to draw a figure. If not possible, write not possible.

1. A triangle with exactly two lines of symmetry. 2. A quadrilateral with exactly two lines of symmetry

3. A pentagon with exactly two lines of symmetry. 4. A hexagon with exactly two lines of symmetry. Name: ______Date: ______Block: ______5. An octagon with exactly two lines of symmetry. 6. A quadrilateral with exactly four lines of symmetry.

Example 3: Determine whether the entire word has line symmetry and whether it has rotational symmetry. Identify all lines of symmetry and angles of rotation that map the entire word onto itself.