2.4 Synchronous Parallelism

Section 2.4 Synchronous Parallelism

2.4.1 Sequential and parallel Jacobi Relaxation programs. parallel computing is playing a more and more important role in the large scale numberical problems arising in science and engineering.

One problem for the parallel computation is that some processes must be synchronized after each iteration because the values produced by one process are used by other processes on the next iteration. This style of parallel programming is called synchronous parallelism.

We will use a standard numerical algorithm called Jacobi Relaxation as an example to solve a differential equation.

1 SOLVING A DIFFERENTIAL EQUATION

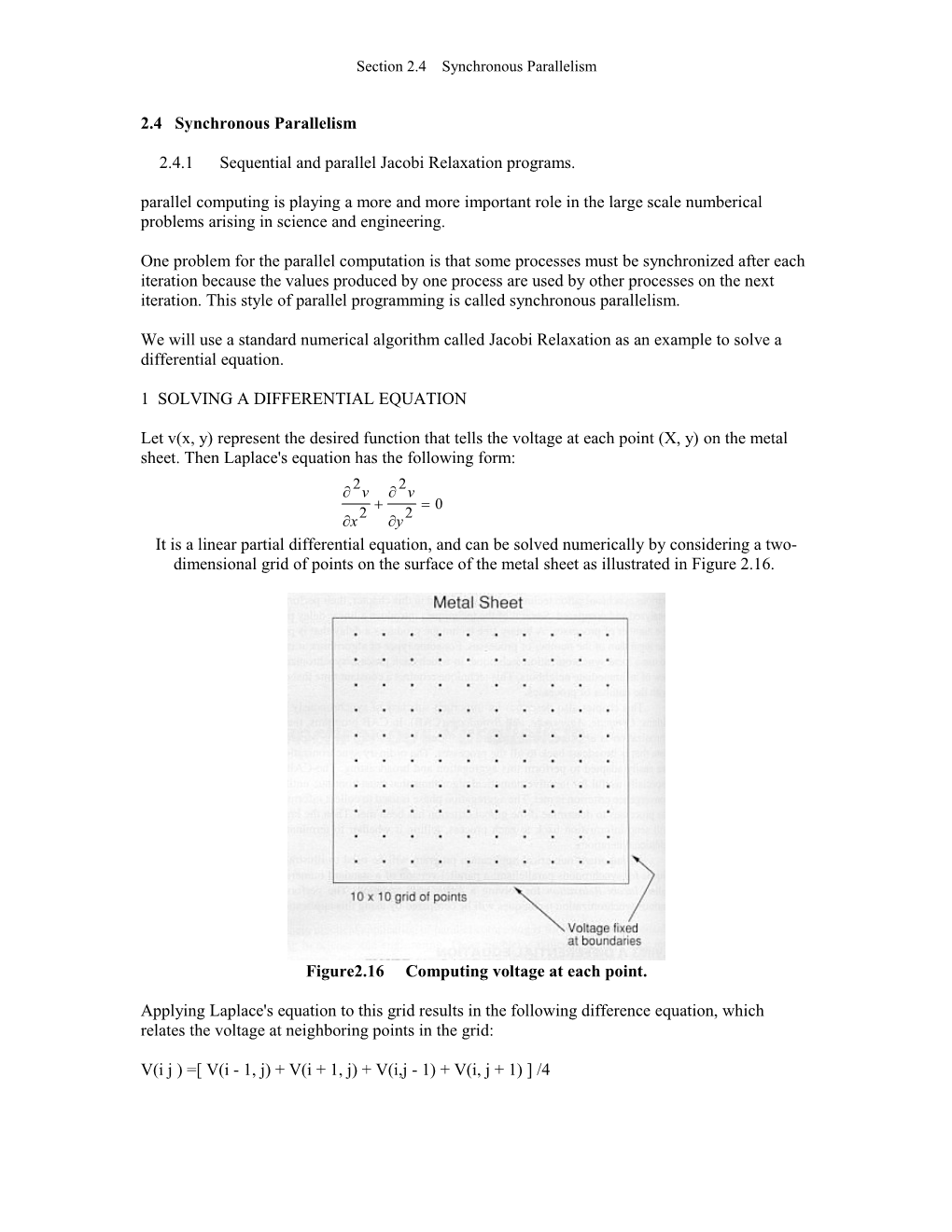
Let v(x, y) represent the desired function that tells the voltage at each point (X, y) on the metal sheet. Then Laplace's equation has the following form: 2 2  v  v   0 2 2 x y It is a linear partial differential equation, and can be solved numerically by considering a two- dimensional grid of points on the surface of the metal sheet as illustrated in Figure 2.16.

Figure2.16 Computing voltage at each point.

Applying Laplace's equation to this grid results in the following difference equation, which relates the voltage at neighboring points in the grid:

V(i j ) =[ V(i - 1, j) + V(i + 1, j) + V(i,j - 1) + V(i, j + 1) ] /4 Section 2.4 Synchronous Parallelism

This provides a the relationship between the voltages at neighboring points: the voltage at each point is simply the average of the voltage at its four neighboring points. This relationship is illustrated in Figure 2.17

Figure 2.17 Computing voltage at each point.

The difference equation provides a simple computational technique for solving the equation. The first step is to select some initial values for the voltage at each point on the grid. Since the voltage at all the boundary points is held constant, then these voltages are already known. The initial value for all the internal points can be arbitrarily set to zero initially. Then the following iteration is repeated many times on these values: recompute the value at each point in the grid from the average of its four neighboring points. This computational method is called Jacobi Relaxation. Figure 2.17 also illustrates the general idea behind this method. The sequential Jacobi Relaxation program is given as below:

PROGRAM Jacobi; CONST n=32; (*Size of the array*) numiter=. . . ; (*Number of iterations*) VAR A, B: ARRAY [0..n+1, 0..n+1] OF REAL; i, j, k: INTEGER;

BEGIN FOR i:=0 TO n+1 DO (*Initialize array values*) BEGIN FOR j:=0 TO n+1 DO Read(A[i, j]); Readln; END; B:=A; FOR k:=1 TO numiter DO BEGIN FOR i:=1 TO n DO FOR j:=1 TO n DO (*Compute average of four neighbors*) B[I, j]:=(A[i-1, j]+A[i+1, j]+A[i, j-1]+A[i, j+1])/4; A:=B; Section 2.4 Synchronous Parallelism

END; END. Figure 2.18 Sequential Jacobi Relaxation program

2.4.2 PARALLEL JACOBI RELAXATION

The most obvious technique for parallelizing the Jacobi Relaxation is to change the inner FOR loops to FORALL loops. This will create parallelism during each iteration. The outer FOR loop cannot be changed into FORALL because the iterations must be sequential. A second technique for parallelizing this program is to pull the outer iterative loop inside the parallel processes. Each process will continue to iterate internally, but will synchronize with all other processes at the end of each iteration.

The parallel Jacobi Relaxation program is shown below:

PROGRAM ParallelJacobi; CONST n=32; Numiter = . . . ; VAR A, B: ARRAY [0..n+1, 0.. n+1] OF REAL; i , j, k: INTEGER;

BEGIN . . . (*Read in initial values for array A*)

B := A; FOR k:=1 TO numiter DO BEGIN

(*Phase I - Compute new values*) FORALL i :=1 TO n DO (*Create process for each row*) VAR j: INTEGER; BEGIN FOR j:= 1 TO n DO B[i ,j] := (A [i -1, j] + A[i , j-1] + A[i , j-1] +A[i , j+1]) /4 ; END;

(*Phase II - Copy new values back to A*) FORALL i := 1 TO n DO (*Copy new values from B back to A*) A[i ] := B[i ];

END; END.

The parallel version of the Jacobi Relaxation basically requires each iteration to be completed before the next one begins. To avoid the granularity problem, we create a process to handle each row of points by parallelizing the i loop only. The inner index j must be changed into a local variable within each process. Section 2.4 Synchronous Parallelism

The process synchronization is achieved by allowing the processes to terminate and then recreating them again in this parallel Jacobi Relaxation program. There are two such synchronizations during each iteration: one after Phase I and another after Phase II. During Phase I, the first set of 32 processes is created by the first FORALL to operate on the 32 rows of the array. A. The FORALL statement terminates only after all 32 processes terminate. Therefore, the structure of the FORALL statement itself is used to synchronize the processes.

For a program with n processes, this synchronization method has execution time O(n).

2.4.3 Barrier Synchronization

Due to the considerable large overhead of process creation, the approach of terminating and then recreating processes is unacceptable in many systems. Barrier operation is way to provide cheaper synchronization of processes. A Barrier is a point in the program where parallel processes wait for each other. The effect of Barrier is illusrated in Figure 2.20:

FIGURE 2.20 Barrier synchronization of processes.

We can apply the Barrier synchronization technique to the Parallel Jacobi Relaxation as follows:

PROGRAM Jacobi_Barrier; CONST n = 32; Numiter = … ; VAR a, b: ARRAY [0.. n+1, 0..n+1] OF REAL; i , j: INTEGER;

BEGIN . . . (*Read in initial values for array A*)

B:=A; FORALL i := 1 TO n DO (*Create one process for each row*) VAR j, k: INTEGER; Section 2.4 Synchronous Parallelism

BEGIN FOR k:= 1 TO numiter DO BEGIN FOR j:= 1 TO n DO (*Compute average of four neighbors*) B[i , j] := (A[i +1, j] + A[i , j-1] +A[i , j+1] /4 ; Barrier; A[i ] := B[i ]; Barrier; END; END; END. FIGURE 2.21 Jacobi Relaxation with Barrier synchronization.

Here only one set of processes is created initially, instead of terminating and recreating the processes. The performance of the program is highly dependent on the time required to execute the Barrier operation.

2.4.4 Linear Barrier Implement

We can use spinlocks or channels to implement the Barrier operation since Multi-Pascal programming language does not have an explicit Barrier statement. One implementation using spinlocks is shown below:

PROGRAM Jacobi_Barrier; CONST n=32;

VAR . . .

count : INTEGER; Arrival, Departure: SPINLOCK;

PORCEDURE Barrier; BEGIN

(*Arrival Phase – Count the processes as they arrive*) Lock(Arrival); count := count +1; IF count < n THEN Unlock(Arrival) (*continue Arrival Phase*) ELSE Unlock(Departure); (*terminate Arrival Phase*)

(*Departure Phase – Count the processes as they leave*) Lock(Departure); count := count –1 ; IF count > 0 THEN Unlock(Departure) (*continue Departure Phase*) ELSE Unlock(Arrival); (*terminate Departure Phase*)

END; Section 2.4 Synchronous Parallelism

BEGIN (*Main Program*) count := 0; (*Initialize “count” and spinlocks*) Unlock(Arrival); Lock(Departure); . . . END. FIGURE 2.22 Barrier implemented with spinlocks.

There are two distinct phases in the Barrier procedure. During the Arrival Phase, processes are counted as they arrive at the Barrier. After all the processes have arrived, the Arrival Phase is terminated, and the Departure Phase begins. During the Departure Phase, the processes are released from the Barrier one at a time. Counting also occurs during the Departure Phase, so it will be known when all the processes have been released. To separate the activity of the phases, two different spinlocks are used: arrival and Departure. Each spinlock is used to make the counting an atomic operation during their corresponding phases. Also please note the unusual use of "Unlock" at the end of each atomic operation. This is done by keeping the spinlock Departure in the "locked" state during the Arrival Phase. For this double-locking mechanism to work correctly, spinlock Arrival must be initially “unlocked” and Departure must be initially “locked”. The performance of this Barrier implementation is limited by the contention for the count variable during the atomic increment and atomic decrement operation. The counting variable method has execution time O(n).