Homework 10 Solutions Statistics 112 – Spring 2004
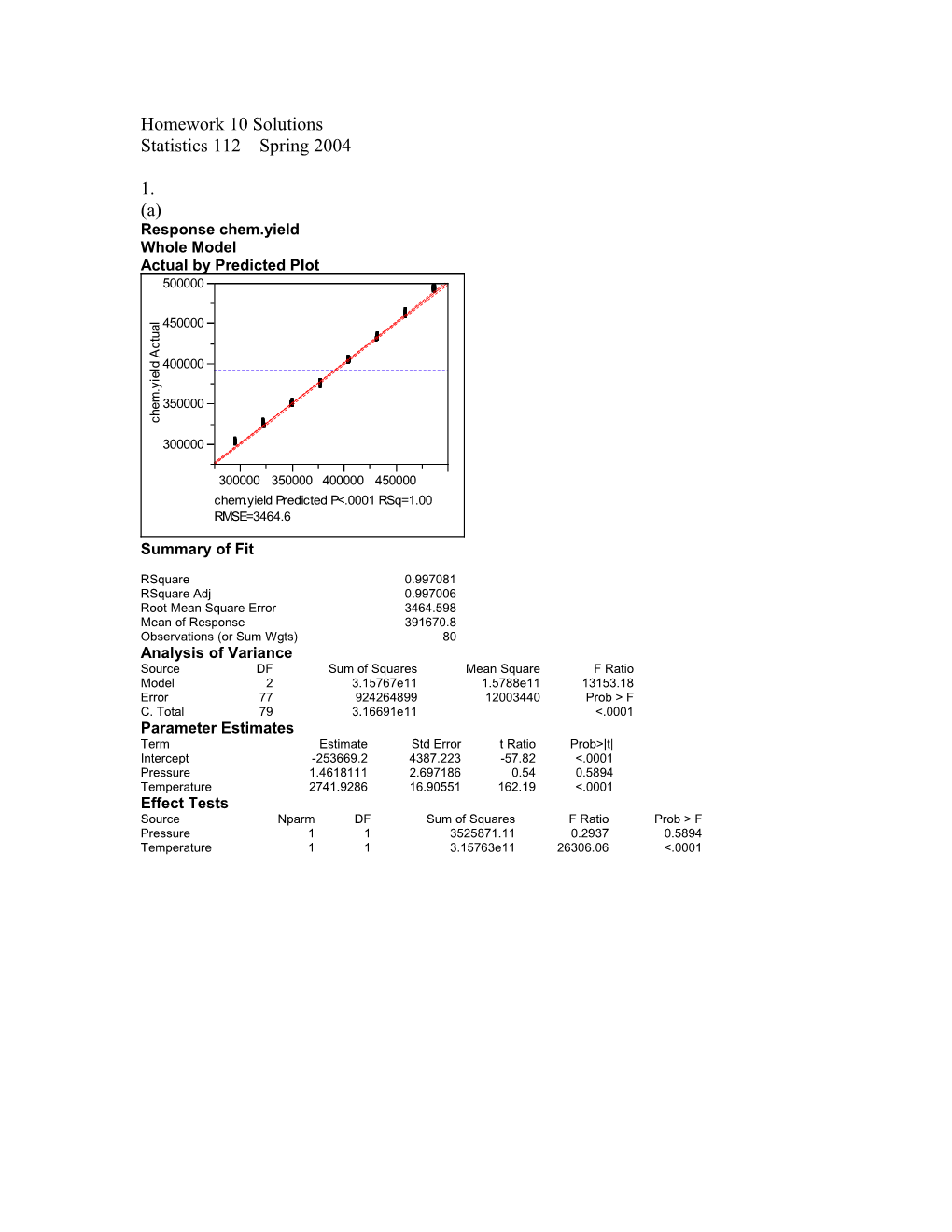
1. (a) Response chem.yield Whole Model Actual by Predicted Plot 500000
l 450000 a u t c A
d 400000 l e i y . m
e 350000 h c
300000
300000 350000 400000 450000 chem.yield Predicted P<.0001 RSq=1.00 RMSE=3464.6
Summary of Fit
RSquare 0.997081 RSquare Adj 0.997006 Root Mean Square Error 3464.598 Mean of Response 391670.8 Observations (or Sum Wgts) 80 Analysis of Variance Source DF Sum of Squares Mean Square F Ratio Model 2 3.15767e11 1.5788e11 13153.18 Error 77 924264899 12003440 Prob > F C. Total 79 3.16691e11 <.0001 Parameter Estimates Term Estimate Std Error t Ratio Prob>|t| Intercept -253669.2 4387.223 -57.82 <.0001 Pressure 1.4618111 2.697186 0.54 0.5894 Temperature 2741.9286 16.90551 162.19 <.0001 Effect Tests Source Nparm DF Sum of Squares F Ratio Prob > F Pressure 1 1 3525871.11 0.2937 0.5894 Temperature 1 1 3.15763e11 26306.06 <.0001 Pressure Leverage Plot s
l 500000 a u d i s
e 450000 R
e g a r 400000 e v e L
d
l 350000 e i y . m
e 300000 h c
400 500 600 700 800 900 Pressure Leverage, P=0.5894
Temperature Leverage Plot s
l 500000 a u d i s
e 450000 R
e g a r 400000 e v e L
d
l 350000 e i y . m
e 300000 h c
190 200 210 220 230 240 250 260 270 280 Temperature Leverage, P<.0001
(b) Residual by Predicted Plot
5000 l a u d i s e R
0 d l e i y . m
e -5000 h c
-10000 300000 350000 400000 450000 chem.yield Predicted Fit Y by X Group Bivariate Fit of Residual chem.yield By Pressure
5000 d l e i y . m
e 0 h c
l a u d i s e -5000 R
-10000 400 500 600 700 800 900 Pressure
Bivariate Fit of Residual chem.yield By Temperature
5000 d l e i y . m
e 0 h c
l a u d i s e -5000 R
-10000 190 200 210 220 230 240 250 260 270 280 Temperature
Distributions Residual chem.yield
-10000 -5000 0 5000 Cook's D Influence chem.yield
-0.01 .01 .02 .03 .04 .05 .06 .07 .08 .09 .1
The residual plots of residuals by predicted and residuals by temperature show a quadratic which indicates that there is a violation of the linearity assumption. However, the residual plots do not show any indication that the variance is non-constant. The distribution of residuals is approximately normal and there are no outliers. There are no influential observations as can be seen in the histogram of the Cook’s distances since there are no Cook’s distances greater than 1.
(c) Examining the residual plots shows that temperature has a quadratic relationship with chemical yield, thus x1=temperature and x2=pressure.
Response chem.yield Whole Model Summary of Fit
RSquare 0.999155 RSquare Adj 0.999121 Root Mean Square Error 1876.751 Mean of Response 391670.8 Observations (or Sum Wgts) 80 Analysis of Variance Source DF Sum of Squares Mean Square F Ratio Model 3 3.16423e11 1.0547e11 29945.65 Error 76 267686863 3522195.6 Prob > F C. Total 79 3.16691e11 <.0001 Parameter Estimates Term Estimate Std Error t Ratio Prob>|t| Intercept 88291.257 25158.56 3.51 0.0008 Pressure 1.4618111 1.461049 1.00 0.3202 Temperature -196.3054 215.3986 -0.91 0.3650 temp^2 6.2515619 0.45788 13.65 <.0001 Effect Tests Source Nparm DF Sum of Squares F Ratio Prob > F Pressure 1 1 3525871 1.0010 0.3202 Temperature 1 1 2925449 0.8306 0.3650 temp^2 1 1 656578036 186.4116 <.0001 (d) Response chem.yield Whole Model Summary of Fit
RSquare 0.999212 RSquare Adj 0.99917 Root Mean Square Error 1824.625 Mean of Response 391670.8 Observations (or Sum Wgts) 80 Analysis of Variance Source DF Sum of Squares Mean Square F Ratio Model 4 3.16441e11 7.911e+10 23762.16 Error 75 249694267 3329256.9 Prob > F C. Total 79 3.16691e11 <.0001 Parameter Estimates Term Estimate Std Error t Ratio Prob>|t| Intercept 88291.257 24459.79 3.61 0.0006 Pressure 1.4618111 1.420469 1.03 0.3067 Temperature -196.3054 209.4159 -0.94 0.3516 temp^2 6.2515619 0.445163 14.04 <.0001 (Pressure-675)*(Temperature-235) 0.1441203 0.061994 2.32 0.0228 Effect Tests Source Nparm DF Sum of Squares F Ratio Prob > F Pressure 1 1 3525871 1.0591 0.3067 Temperature 1 1 2925449 0.8787 0.3516 temp^2 1 1 656578036 197.2146 <.0001 Pressure*Temperature 1 1 17992596 5.4044 0.0228
There is evidence of an interaction between pressure and temperature. The t-test (with a null hypothesis that the parameter equals 0) has p-value 0.0228, thus there is statistical evidence of an interaction between pressure and temperature. 2. (a) Scatterplot Matrix 1100 1000 MORT 900 800 70 50 PRECIP 30 10 12.0 11.0 EDUC 10.0 9.0 35 25 NONWHITE 15 5 350 250 NOX 150 50
250 150 SO2 50
800 950 1100 10 30 50 709.0 10.5 12.0 5 15 25 35 50 15025035050 150 250
(b) Looking at the scatter-plot of mort vs. NOX, doing a log transformation of NOX is a good idea because the observations are crunched together and positive. Doing the transformation will spread them out. The scatter-plot of mort vs. SO2 shows that there is a nonlinear relationship between S02 and MORT. Tukey’s bulging rule indicates that the log transformation is a good transformation to try to remove the nonlinearity (the shape of the curvature is in the upper left quadrant of the circle for Tukey’s bulging rule). (c) Response MORT Whole Model Actual by Predicted Plot 1150 1100
l 1050 a u t 1000 c A
T 950 R
O 900 M 850 800 750 750 800 850 900 950 100010501100 MORT Predicted P<.0001 RSq=0.69 RMSE=36.301
Summary of Fit
RSquare 0.688278 RSquare Adj 0.659415 Root Mean Square Error 36.30065 Mean of Response 940.3568 Observations (or Sum Wgts) 60 Analysis of Variance Source DF Sum of Squares Mean Square F Ratio Model 5 157115.28 31423.1 23.8462 Error 54 71157.80 1317.7 Prob > F C. Total 59 228273.08 <.0001 Parameter Estimates Term Estimate Std Error t Ratio Prob>|t| Intercept 940.6541 94.05424 10.00 <.0001 PRECIP 1.9467286 0.700696 2.78 0.0075 EDUC -14.66406 6.937846 -2.11 0.0392 NONWHITE 3.028953 0.668519 4.53 <.0001 log NOX 6.7159712 7.39895 0.91 0.3681 log S02 11.35814 5.295487 2.14 0.0365 Effect Tests Source Nparm DF Sum of Squares F Ratio Prob > F PRECIP 1 1 10171.388 7.7188 0.0075 EDUC 1 1 5886.913 4.4674 0.0392 NONWHITE 1 1 27051.227 20.5285 <.0001 log NOX 1 1 1085.691 0.8239 0.3681 log S02 1 1 6062.217 4.6005 0.0365 Residual by Predicted Plot 100
l 50 a u d i s
e 0 R
T R
O -50 M
-100
750 800 850 900 950 100010501100 MORT Predicted After running the model, the Cook’s distances are computed. New Orleans has a distance greater than 1 (D=1.75) which means that it is influential. This point also has high leverage, which is realized by comparing the leverage (.454 from JMP) to the value of 2*p/n (=.167). New Orleans is influential and has high leverage so it is justified to remove it from the analysis and report the results for a reduced range of explanatory variables. The removal of New Orleans also changes the significance of the education variable, so using Display 11.8 we can also see that excluding New Orleans is justified.
3. (a) Note: with New Orleans removed
Response MORT Parameter Estimates Term Estimate Std Error t Ratio Prob>|t| Lower 95% Upper 95% Intercept 909.9347 92.44838 9.84 <.0001 724.24673 1095.6228 8 PRECIP 0.606978 1.004941 0.60 0.5486 -1.411505 2.6254621 7 EDUC -8.050719 6.593477 -1.22 0.2278 -21.29411 5.1926688 NONWHITE 2.650649 0.626042 4.23 <.0001 1.3932063 3.9080926 5 log NOX -32.41826 15.36709 -2.11 0.0399 -63.28396 -1.552557 log S02 39.58033 17.71913 2.23 0.0300 3.9904169 75.170259 8 log NOX*log S02 -0.493481 2.434972 -0.20 0.8402 -5.384267 4.397305 log NOX*precip 1.050122 0.489055 2.15 0.0366 0.0678267 2.0324182 4 log S02*precip -0.59979 0.457222 -1.31 0.1956 -1.518146 0.3185668
The interaction between precipitation and NOX is significant (p-value=0.037), while the interactions Precipitation*SO2 and SO2*NOX are not significant (p-values of 0.196 and 0.840 respectively). The impact on mortality due to an increase in NOX depends on the level of precipitation.
(b) Statistical findings: There is strong evidence that when precipitation, education, nonwhite and NOX are held fixed, increases in SO2 are associated with increases in mortality (p- value =.035). The model estimates that a one unit increase in the log of SO2 is associated with an increase in the mean mortality rate of 16.19 (95% CI: 1.22, 31.17). There is no evidence that the impact of sulfur dioxide on mortality depends on the level of precipitation nor on the level of nitrogen (interaction terms have p-values of 0.196 and 0.840 respectively). There is strong evidence that when precipitation, education, nonwhite and S02 are held fixed, increases in NOX are associated with mortality in a way that interacts with precipitation. The p-value on the interaction term between log NOX*precip is .0366. The model estimates that a one unit increase in log NOX is associated with a –32.41+1.05*precip change in mortality (thus, depending on the precipitation level, the association can be positive or negative).
Scope of inference: The conclusions above apply only to a limited range of explanatory variables that excludes the explanatory variable values exhibited by New Orleans; we removed New Orleans because it was highly influential and had high leverage. The inferences above about the associations between pollution and mortality can only be considered causal inferences about the impact of changing pollution (and holding everything else fixed) on mortality if there are no omitted confounding variables (we controlled for the confounding variables median education, precipitation and percentage nonwhite). The inferences cannot be considered to apply to a wider population unless the cities were randomly sampled.
4. (a) Response Absent Whole Model - Actual by Predicted Plot 16 14
l 12 a u t c 10 A
t n
e 8 s b
A 6 4 2 0 2 4 6 8 10 12 14 16 Absent Predicted P<.0001 RSq=0.53 RMSE=2.3559
Summary of Fit
RSquare 0.532348 RSquare Adj 0.507473 Root Mean Square Error 2.35589 Mean of Response 6.232 Observations (or Sum Wgts) 100 Analysis of Variance Source DF Sum of Squares Mean Square F Ratio Model 5 593.8972 118.779 21.4009 Error 94 521.7204 5.550 Prob > F C. Total 99 1115.6176 <.0001 Parameter Estimates Term Estimate Std Error t Ratio Prob>|t| Lower 95% Upper 95% Intercept 10.264794 1.17237 8.76 <.0001 7.9370264 12.592562 Wage -0.000203 0.000036 -5.69 <.0001 -0.000274 -0.000132 Pct PT -0.106871 0.029492 -3.62 0.0005 -0.165429 -0.048313 Pct U 0.0598537 0.012403 4.83 <.0001 0.0352264 0.0844811 Av Shift 1.561942 0.502656 3.11 0.0025 0.5639071 2.559977 U/M Rel -2.636646 0.492175 -5.36 <.0001 -3.61387 -1.659421 Effect Tests Source Nparm DF Sum of Squares F Ratio Prob > F Wage 1 1 179.72691 32.3820 <.0001 Pct PT 1 1 72.87995 13.1310 0.0005 Pct U 1 1 129.24349 23.2862 <.0001 Av Shift 1 1 53.59179 9.6558 0.0025 U/M Rel 1 1 159.28498 28.6989 <.0001 Residual by Predicted Plot 8 6 l a
u 4 d i s
e 2 R
t
n 0 e s b
A -2 -4 -6 0 2 4 6 8 10 12 14 16 Absent Predicted
The average number of days absent per employee is estimated as being 2.64 days lower when there is a good union/management relationship. The 95% CI for this difference is (1.66, 3.61). This confidence interval does not contain 0, so there is a significant difference in absenteeism for these groups (also p-value for the parameter is <0.0001).
(b) Yes. Assuming there are no omitted confounding variables, a negative coefficient on the union/management relationship variable means that improving union/management relations would cause a decrease in mean absenteeism. The 95% confidence interval for the coefficient on the union/management relationship is (-1.66, -3.61), meaning that there is strong evidence that the coefficient is less than zero. The p-value for the two-sided test is <.0001. Thus, assuming there are no omitted confounding variables, there is strong evidence that improving union-management relationships would cause a decrease in mean absenteeism.