Model Adequacy Checking

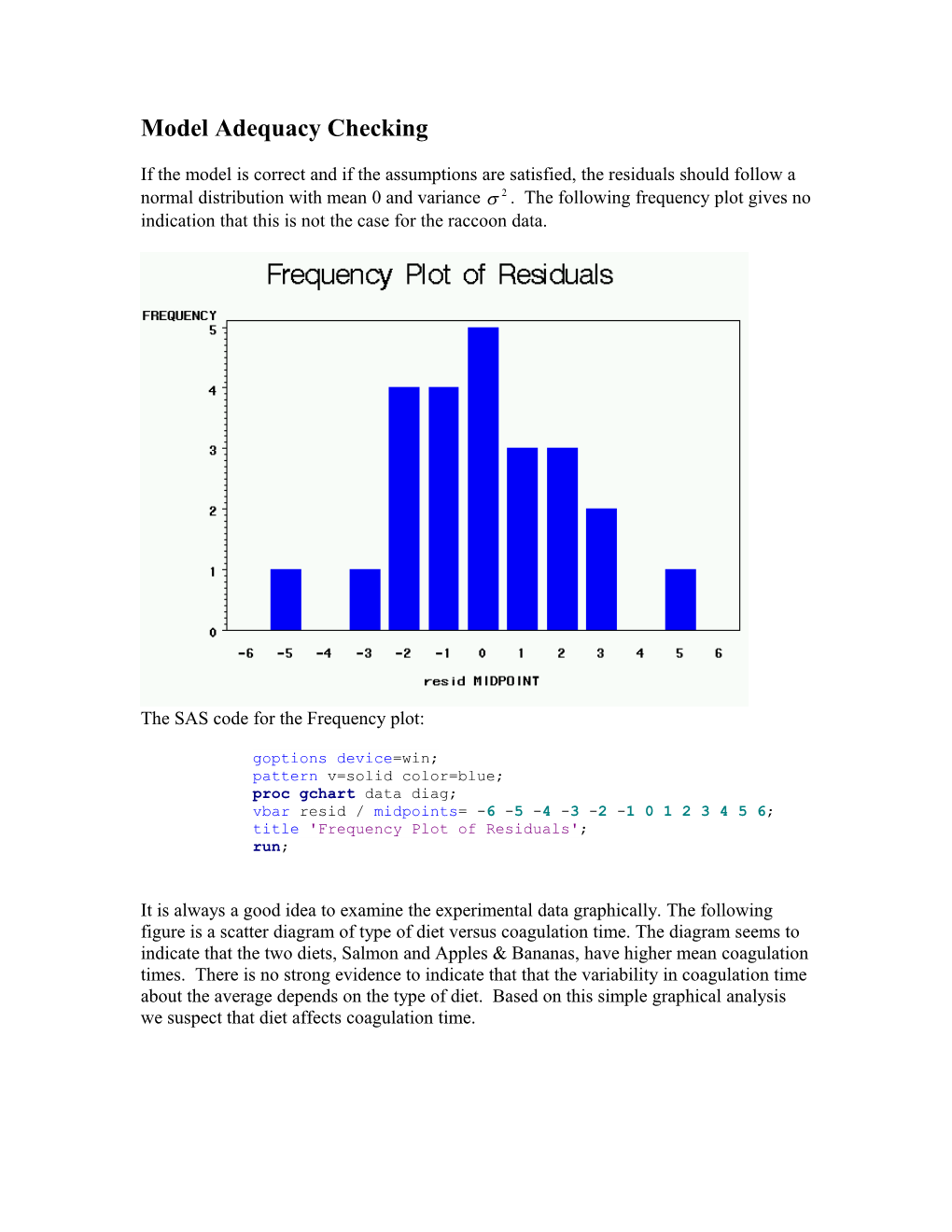
If the model is correct and if the assumptions are satisfied, the residuals should follow a normal distribution with mean 0 and variance s 2 . The following frequency plot gives no indication that this is not the case for the raccoon data.

The SAS code for the Frequency plot:

goptions device=win; pattern v=solid color=blue; proc gchart data diag; vbar resid / midpoints= -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6; title 'Frequency Plot of Residuals'; run;

It is always a good idea to examine the experimental data graphically. The following figure is a scatter diagram of type of diet versus coagulation time. The diagram seems to indicate that the two diets, Salmon and Apples & Bananas, have higher mean coagulation times. There is no strong evidence to indicate that that the variability in coagulation time about the average depends on the type of diet. Based on this simple graphical analysis we suspect that diet affects coagulation time. The SAS code for Diet vs. Coagulation Time:

symbol1 v=dot h=.6 c=red; proc gplot data=coons; plot diet*time; title 'Plot of Coon Diet vs. Coagulation Time'; run;

In the following box plot the lines through the boxes mark the medians and the plus signs are the means. The SAS code for the Box Plots:

proc sort data=coons; by diet; run;

symbol color = salmon; title 'Box Plot for Coagulation Times'; proc boxplot data=diag; plot resid*diet / cframe = vligb cboxes = dagr cboxfill = ywh; run; The next graph shows a plot of the diet versus the residuals. Within groups the residuals should be normal 0, s 2 . With small samples considerable fluctuation often occurs, so the appearance of a moderate departure from normality does not necessarily imply a serious violation of the assumptions. In the current case there does not appear to be a problem. SAS code for Diet vs. Residuals plot:

symbol1 v=dot h=.6 c=green; proc gplot data=diag; plot diet*resid; title 'Plot of Coon Diet vs. Residuals'; run;

Plotting residuals in time order of data collection is helpful in detecting correlation between the residuals. A tendency to have runs of positive and negative residuals indicates a positive correlation. This would imply that the independence assumption on the errors has been violated. Proper randomization of the experiment is an important step in obtaining independence. Sometimes the skill of the experimenter (or the subjects) may change as the experiment progresses, or the process being studied my drift or become more erratic. For instance if a machine were being used to generate the samples, the machines characteristics may change as it heats up. This condition often leads to a plot of residuals verses time that exhibits more spread at one end than at the other. Looking at the above plot, there seems to be no reason to suspect any such effect for the coagulation data, i.e., no violation of independence or constant variance.

SAS code for Order Collected graph (above):

symbol1 v=dot h=.6 c=blue; proc gplot data=diag; plot resid*order; title 'Residuals Plotted in Time Sequence'; run; If the assumptions are satisfied, the residuals should be structureless; in particular, they should be unrelated to any other variable including the predicted response. A simple Xˆ = X check is to plot the residuals versus the fitted values i jg j . This plot should not reveal any obvious pattern. The above plots the residuals versus the fitted values for the coon diet data. No unusual structure is apparent.

The SAS code for the Residual vs. Predicted plot (above) is:

proc gplot data=diag; title 'Residual vs. Predicted Plot'; symbol v=circle h=1; plot resid*pred / haxis=60 61 62 65 66 67 68 69; run; A very common defect that often shows up on normal probability plots is one residual that is very much larger than any of the others. Such a residual is called an outlier. The presence of one or more outliers can seriously distort the ANOVA. So when a potential outlier is located, careful investigation is called for. If the point pattern is nonlinear it usually indicates a departure from normality. For example if the point pattern is curved with slope increasing from left to right, a theoretical distribution that is skewed to the right, such as a lognormal distribution, should provide a better fit than the normal distribution. For our coagulation time data the residuals appear normal.

The following SAS code produced the above Normal probability plot:

symbol v=plus; title 'Normal Probability Plot for Residuals'; proc capability data=diag noprint; probplot resid / cframe = ligr; run;