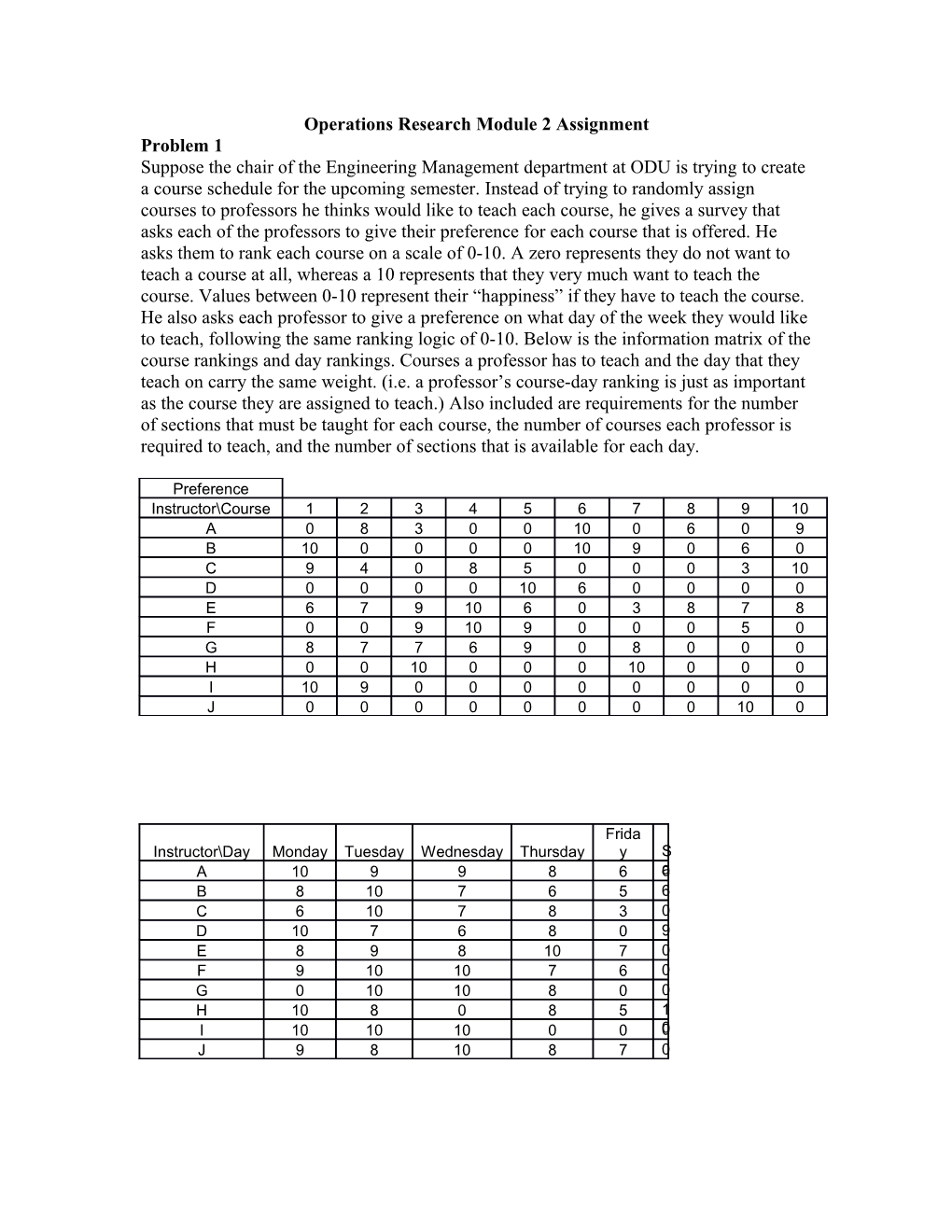
Operations Research Module 2 Assignment

Operations Research Module 2 Assignment Problem 1 Suppose the chair of the Engineering Management department at ODU is trying to create a course schedule for the upcoming semester. Instead of trying to randomly assign courses to professors he thinks would like to teach each course, he gives a survey that asks each of the professors to give their preference for each course that is offered. He asks them to rank each course on a scale of 0-10. A zero represents they do not want to teach a course at all, whereas a 10 represents that they very much want to teach the course. Values between 0-10 represent their “happiness” if they have to teach the course. He also asks each professor to give a preference on what day of the week they would like to teach, following the same ranking logic of 0-10. Below is the information matrix of the course rankings and day rankings. Courses a professor has to teach and the day that they teach on carry the same weight. (i.e. a professor’s course-day ranking is just as important as the course they are assigned to teach.) Also included are requirements for the number of sections that must be taught for each course, the number of courses each professor is required to teach, and the number of sections that is available for each day.

Preference Instructor\Course 1 2 3 4 5 6 7 8 9 10 A 0 8 3 0 0 10 0 6 0 9 B 10 0 0 0 0 10 9 0 6 0 C 9 4 0 8 5 0 0 0 3 10 D 0 0 0 0 10 6 0 0 0 0 E 6 7 9 10 6 0 3 8 7 8 F 0 0 9 10 9 0 0 0 5 0 G 8 7 7 6 9 0 8 0 0 0 H 0 0 10 0 0 0 10 0 0 0 I 10 9 0 0 0 0 0 0 0 0 J 0 0 0 0 0 0 0 0 10 0

Frida Instructor\Day Monday Tuesday Wednesday Thursday y S A 10 9 9 8 6 0a B 8 10 7 6 5 6 C 6 10 7 8 3 0 D 10 7 6 8 0 9 E 8 9 8 10 7 0 F 9 10 10 7 6 0 G 0 10 10 8 0 0 H 10 8 0 8 5 1 I 10 10 10 0 0 0 J 9 8 10 8 7 0 Course # Sections 1 2 2 1 3 2 4 1 5 2 6 1 7 3 8 2 9 1 10 1

Instructor # of Courses Required to teach 1 1 2 1 3 2 4 2 5 2 6 1 7 2 8 1 9 2 10 2

Day Slots Available Monday 2 Tuesday 4 Wednesday 3 Thursday 3 Friday 2 Saturday 2

A. Formulate the problem as an assignment model, show all decision variables and constraints. Formulate the problem such that the average “happiness” of the department is maximized.

B. What is the average “happiness” of each professor in terms of their course load? What is the average “happiness” of each professor in terms of the day of the week that they teach? What is the average total “happiness” (e.g. courses and days) of each professor? What is average “happiness” of the entire department? What professor has the lowest average total “happiness” and what is that value?

C. Create a schedule that gives the maximum average “happiness” of the department.

Problem 2. Draw the Minimum Spanning Tree and provide the required distance to span the network.

Distance = ______

Problem 3. A thief breaks into a house. He searches and finds many items of value. He carries with him a sack that can hold 8 cubic feet of items and he can carry 100 pounds of stolen goods in his sack. He estimates that if he is in the house longer than four minutes he will get caught, he wants to leave before this happens? The following table contains information about each of the items he can acquire.

Item Number Size Ft^3 Weight lbs Time to Steal (Seconds) Profit $ Ring 3 0.25 1 40 250 DVD Player 2 1 10 30 80 Radio 1 1 8 20 50 Elvis Portrait 1 3 20 30 400 42" LCD 1 5 40 50 600 Laptop 1 1 10 40 450 Bucket of Change 1 1 50 20 350 Jade Statue 2 2 35 15 400 DVD's 20 0.25 0.3 10 8 CD's 50 0.25 0.3 10 5

A. Formulate the problem as an integer programming problem. Specify the complete model including all decision variables and constraints. B. Specify what items and how many of each the thief should steal. C. What is the limiting constraint(s), the size of the sack, the weight he can carry, or the amount of time that he has. D. What is his profit for this endeavor?

Problem 4. A city is reviewing the location of its fire stations. The city is made up of a number of neighborhoods, as illustrated in Figure 1. A fire station can be placed in any neighborhood. It is able to handle the fires for both its neighborhood and any adjacent neighborhood. The objective is to minimize the number of fire stations used. Figure 1

A. Formulate the problem as a binary-integer programming problem. Specify the complete model including all decision variables and constraints. B. Specify what neighborhoods should contain a fire station. C. In addition to part B, give two more feasible solutions to this problem. Which solution is best, justify.

Problem 5. The Wythe county supervisor’s board has decided that a new fire station and ambulance facility needs to be built in the county. The county has 30 rural towns that need to be served. A 10 X 10 mile grid has been overlaid on the county map and each of the towns assigned a set of X,Y coordinates. The coordinates of each town along with the expected number of annual trips to each are shown in the following table. Assume that the distance between the facility and rural town is a straight line shortest distance. (The use of the Open Office Non-linear Solver may be required to solve the problem, the Min and Max for the X,Y coordinates of the facilities are between 0 and 10.)

Town X Y # Trips 1 9.2 8.2 63 2 7.6 1.3 85 3 8.9 6.3 33 4 0.7 0.4 14 5 2.2 5.5 5 6 8 1.3 11 7 0.8 3.6 79 8 4.8 8.2 61 9 0.8 9.5 30 10 8.7 4.3 15 11 3.9 9.7 65 12 6.7 1.1 51 13 2.4 8.5 5 14 6.9 2 69 15 2.1 0.2 14 16 0.1 1.3 71 17 6.9 2.4 24 18 4.1 3.4 60 19 4.1 7.1 38 20 7.4 1.1 91 21 8.4 3.3 84 22 0.2 6.2 99 23 4 4.1 39 24 2.4 6.7 56 25 2.8 6.1 33 26 6 2.6 42 27 8.9 8.4 33 28 5.9 7.9 38 29 1.4 8.3 22 30 7.7 3.9 54

1. The county is considering building one facility. A. Formulate the model as a non-linear programming model to answer the following questions. Provide the model and all of the constraints (if necessary). B. Where should the county locate the facility in order to minimize the total distance traveled in one year? (X,Y coordinates) C. What is the total distance traveled in one year? D. Draw a map with the location of each town and the location of the facility. (Use scatter plot in MS Excel or Open Office to draw the map, use Excel template provided). E. What is the average one-way distance for each trip? (Remember, average distance is total distance divided by total number of trips)

2. The county is considering building two facilities. A. Formulate the model as a binary integer non-linear programming model. Provide the model and all of the constraints (if necessary). B. Where should each of the two facilities be located in order to minimize the total distance traveled each year? (X,Y coordinates) C. Assume trips will be made to each town from only one facility. What is the total distance traveled in one year? D. Draw a map with the location of each town and the location of the two facilities. (Use scatter plot in MS Excel or Open Office to draw the map). E. What is the average one-way distance for each trip?

3. The county is considering building three facilities. A. Formulate the model as a binary integer non-linear programming model. Provide the model and all of the constraints (if necessary). B. Where should each of the three facilities be located in order to minimize the total distance traveled each year? C. Assume trips will be made to each town from only one facility. What is the total distance traveled in one year? D. Draw a map with the location of each town and the location of the three facilities. (Use scatter plot in MS Excel or Open Office to draw the map). E. What is the average one-way distance for each trip?