Lesson 15 Linear Equations

GOLD 1

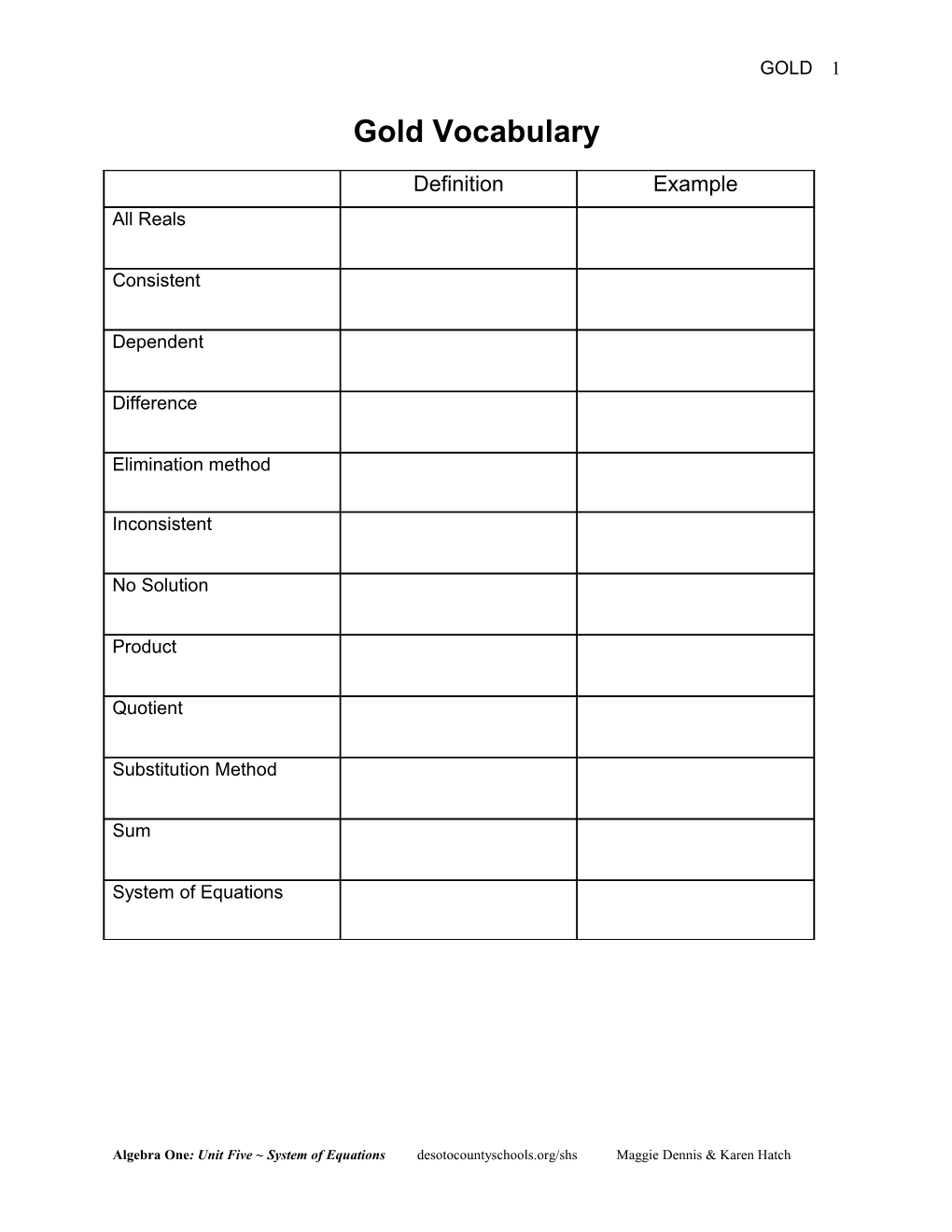
Gold Vocabulary

Definition Example All Reals

Consistent

Dependent

Difference

Elimination method

Inconsistent

No Solution

Product

Quotient

Substitution Method

System of Equations

Algebra One: Unit Five ~ System of Equations desotocountyschools.org/shs Maggie Dennis & Karen Hatch GOLD 2

Lesson 17 Solving Systems of Equations Graphing Notes

Solution Possibilities 1. (2,1)

Lesson 17 Solving Systems of Equations Graphing Notes

y 10 Example One Draw a line with a slope of -3. Draw the graph of a line that is perpendicular to your first line. Write the equation of the perpendicular line.

-10 10 x

y 10 Example Two Graph two lines that intersect at the point (1,4). Write the equations of your lines.

-10 10 x

y 10 Example Three x - 3y = -3 y = 2x - 4

-10 10 x

Lesson 17 Solving Systems of Equations Graphing Notes y 10 Example Four x + y = 0 x + y = 5

-10 10 x

y 10 Example Five y = 4x + 1 12x - 3y = -3

-10 10 x

y 10 Example Six y = -2 2x + y = 8

-10 10 x

Lesson 17 Solving Systems of Equations Graphing

1. How many solutions? 2. How many solutions? Point of Intersection? Point of Intersection? Write the equation for Write the equation for each line. y each line. y 10 10

x x -10 10 -10 10

-10 -10 Change to slope-intercept, graph each equation, and identify the point of intersection by writing it as an ordered pair: 3. y = x + 3 4. 3x – y = 8

-6x + 2y = y-18 y = -x y 10 10

-10 10 x -10 10 x

-10 -10

5. Jessica graphed the following two linear equations on a coordinate grid: 5x + 2y = 4 Hint: Graph both lines. 2x + 5y = 4 Which of the following BEST describes the graph of ythe two linear equations? 10

A) The two lines are parallel B) The two lines are perpendicular C) The two lines are the same

D) The two lines intersect at one point -10 10 x

6. Two lines on a coordinate plane have no points of intersection. Which of the following sets of equations could represent the lines? Hint: Graph all lines. A) 3x + 5y = 5 B) 3x + 5y = 5 6x + 10y = 10 6x + 10y = 5

C) 3x + 5y = 5 D) 3x + 5y = 5 6x – 10y = 10 y 6x – 10y = 5 10

-10 10 x

-10 Algebra One: Unit Five ~ System of Equations desotocountyschools.org/shs Maggie Dennis & Karen Hatch GOLD 7

7. Which point is a solution for BOTH of the following equations? y = 3x – 2 Hint: Graph both lines. 2y = x + 1 A) (1, 1) B) (2, 4) C) (1, 2) D) (0, -2)

-10 10 x

DOK 2 8. Draw a line with a slope of 2. Write the equation of your line. Draw a line that is perpendicular to your first line on the same coordinate plane.

Write the equationy of the perpendicular line. 10

-10 10 x

Algebra One: Unit Five ~ System of Equations desotocountyschools.org/shs Maggie Dennis & Karen Hatch -10 GOLD 8

y 10 9. Draw the graph of a line whose equation 3 is y = x – 1. Draw the graph of a line 2 parallel to this line and write the equation of this line. -10 10 x

y -10 10 10. Draw the graph of a line whose equation 5 is y =  x. Draw the graph of a line 2 perpendicular to this line and write the -10 10 x equation of this line.

y 10 -10 11. Graph two lines that intersect at the point (-2, 3). Write the equations of your lines.

-10 10 x

y 10 -10

12. Graph two lines that are perpendicular to one another and intersect at the origin.

-10 10 x

Lesson 23 Solving Systems of Inequalities Notes The solution to a system of inequalities is not a single ordered pair, but a region of the coordinate plane.

Recall when graphing inequalities we must shade. Example One The solution will be the intersection of the two shaded y > -x + 3 y < (1/4)x - 2 regions.

Example Two 2y + 2x < 6 y > 2x + 2 -10 10 x

Example Three

-10 10 x 3x + 8y > 40 4x - 3y > 6

-10 10 x

Lesson 23 Solving Systems of Inequalities

DOK 1 1. The system of equations 2y = x + 6 and x = -1 is shown on the graph below. Which point satisfies both of the following inequalities, 2y ≤ x + 6 and x ≥ -1? (Hint: add the shading) y 5 a) (-2, 5) b) (-2, 1) x c) (0, 5) -5 5 d) (1, -1)

Match each system of inequalities toy the correct graph: y 5 5 ____ 2. y < ½ x – 1 y ≤ -2x + 2 A ____ 3. y ≤ ½ x + 1 x B x y > -½ x – 2 -5 5 -5 5

____ 4. y ≤ 2x + 2 y > -x – 1 -5 -5 ____ 5. y > x – 2 y y y ≥ -x + 1 5 5 C

x x -5 5 -5 5 D Algebra One: Unit Five ~ System of Equations desotocountyschools.org/shs Maggie Dennis & Karen Hatch -5 -5 GOLD 11

Lesson 23 Solving Systems of Inequalities

DOK 2 y Graph each system of linear inequalities. 10

6. y  -2 y < 2x + 1

-10 10 x

-10y 10 7. y  3x – 2 x  -3

-10 10 x

-10y 10 8. y – 2x < -3 2x + 3y > 3

-10 10 x

-10y 9. 4y – x > 8 5x – 2y > 2 10

-10 10 x

-10 Algebra One: Unit Five ~ System of Equations desotocountyschools.org/shs Maggie Dennis & Karen Hatch GOLD 12

Lesson 19 Solving Systems by Substitution Notes

Use this method when one of your lines is vertical (y= ) or horizontal (x= ). Plug in the value for x (or y) into the other equation and solve. Write your answer as an ordered pair.

Example One x = 8 y = 3x - 3

Example Two

3x - 10y = -80 y = 5

Example Three y = 2 x - 6y = 0

Lesson 19 Solving Systems by Substitution

DOK 1 Write each answer as an ordered pair.

1. x = 4 2. y = -3 4x – 3y = 25 4x – 3y = 25

3. –x + 2y = 0 4. –x + 2y = 0 y = 7 x = 0

5. 4x – y = 9 6. 4x – y = 9 y = 3 y = -3

7. -2y – 5x = 17 8. -2y – 5x = 17 x = 1 y = -6

9. y = 0 10. x = 0 19x – y = 19 19x – y = 19

Lesson 20 Solving Systems of Equations Elimination Notes

Example One Solve the following system: -x + y = 5 x + 2y = -2

Example Two

Solve the following system: 3x + y = -2 -6x - 2y = 4

Example Three Solve the following system: -7x + y = 1 3 - 3y = 7x

Example Four Solve the following system: -x + y = 5 -3x + 3y = -2

Example Five Solve the following system: 9x – 8y = 64 5x + 2y = 42

Lesson 20 Solving Systems of Equations Elimination

DOK 1 Determine if the ordered pair is a solution of the given system. 1. (-4, 2) 4x – 3y = -22 2. (3, -7) x – 5y = 38 2x + y = -6 3x + 4y = -20

3. (-2, 3) 7y = 2x + 25 4. (5, 1) 3y = 4x – 17 3x = 16 – 2y 2x + y = 11

DOK 2 5. At the Burger Palace, 2 hamburgers and 1 small order of fries cost $6.09. The Clarkes ordered 5 hamburgers and 5 small orders of fries and paid $17.95. What was the cost of 1 small order of fries?

6. In Cleo’s class, g, the number of girls, is 3 times b, the number of boys. There are a total of 28 students in the class. Write a system of equations could be used to evaluate this situation to determine the number of boys in Cleo’s class.

7. Greg is going to solve the system of linear equations below. First Equation: 8x - 2 y = 8 Second Equation: 3x + 3 y = 9 Which of the following would Greg NOT use to solve this system of equations? A Solve the second equation for y and then substitute the result into the first equation. B Multiply the first and second equation by -6 to eliminate the y variable. C Solve the first equation for y and then substitute the result into the second equation. D Multiply the first equation by 3 and the second equation by 2 to eliminate the y variable.

Algebra One: Unit Five ~ System of Equations desotocountyschools.org/shs Maggie Dennis & Karen Hatch