Figure 1 Typical Plots of Snapweights Vs Sequence Number for a Single ID

Time Series Models: AR/MA:

To begin, we observe that our data are distributed in time as well as in space. As such, we test out whether or not SnapWeights can be treated as a time series and modeled by a stochastic process evolving in time. Many methodologies for modeling time series data exist but for the purposes of this project, we narrow our scope to models that assume a linear dependence on previous data points and require stationarity and ergodicity. A rigorous explanation of these two properties is beyond the scope of this report.

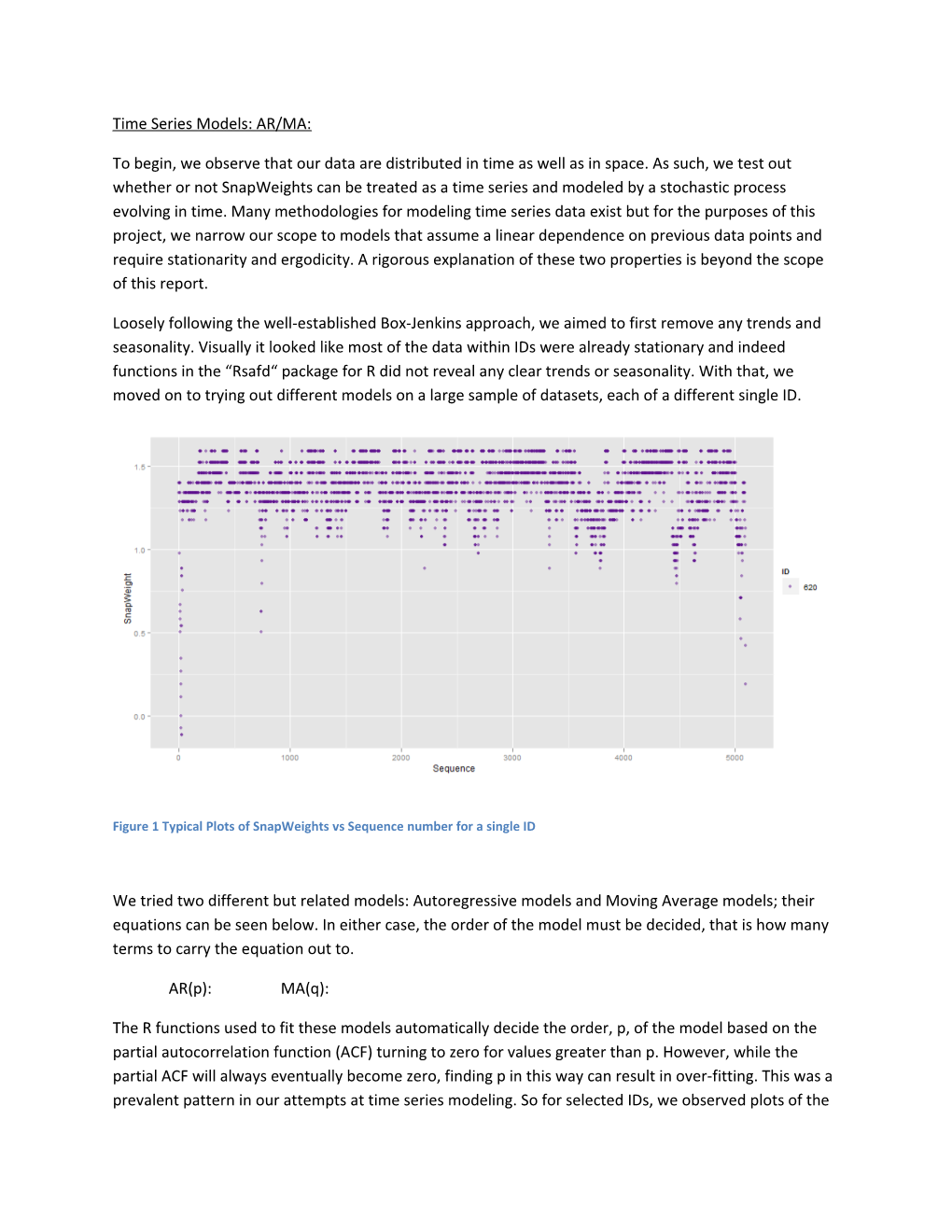
Loosely following the well-established Box-Jenkins approach, we aimed to first remove any trends and seasonality. Visually it looked like most of the data within IDs were already stationary and indeed functions in the “Rsafd“ package for R did not reveal any clear trends or seasonality. With that, we moved on to trying out different models on a large sample of datasets, each of a different single ID.

Figure 1 Typical Plots of SnapWeights vs Sequence number for a single ID

We tried two different but related models: Autoregressive models and Moving Average models; their equations can be seen below. In either case, the order of the model must be decided, that is how many terms to carry the equation out to.

AR(p): MA(q):

The R functions used to fit these models automatically decide the order, p, of the model based on the partial autocorrelation function (ACF) turning to zero for values greater than p. However, while the partial ACF will always eventually become zero, finding p in this way can result in over-fitting. This was a prevalent pattern in our attempts at time series modeling. So for selected IDs, we observed plots of the ACF versus the lag, or the difference between the two times at which points, Xt and Xt+lag, are being observed. This should typically show a rapid exponential decay, but instead most of our graphs, such as the one below, showed rather slow decay, and therefore lower likelihood of good fit using these models.

Figure 2 ACF vs Lag. Slow decay

With widely varying parameters attained in the time series models for different IDs, we decided to use another known heuristic to determine whether continuing to experiment with linear time series models was worthwhile. We sought periodicity in the data sets using a simple Fast Fourier Transform, however, large the majority of plots showed that the data was all noise; a typical example is shown below with its x-axis truncated. With this, and a few very limited attempts with mixed ARMA models that are not worth reporting, we ceased trying to model SnapWeight as a time series.

Figure 3 Plot of Fast Fourier Transform of SnapWeights Clustering IDs using K-Means:

As mentioned (was it mentioned?) our different modeling approaches operate under different sets of assumptions regarding the distribution of the response variable. Assuming Independent and Identically Distributed (I.I.D) data is reasonable given the nature of the GPS signals which they are based on, but the scope in which the data are I.I.D must also be decided. As such there are two different modeling assumptions here: first, that SnapWeights are IID within each particular trip as represented by the ID. The second is that all SnapWeights, irrespective of ID, are I.I.D. We first analyze our data under the stricter first assumption.

We decided to try to join together IDs whose SnapWeights had similar distributions. Our first approach involved using a two-sample Kolmogorov-Smirnov test, which essentially uses a distance metric between two empirical distribution functions. However, implementation problems with this method arose in R, leading us to try using Mutual Information as a criterion instead. Though the MI method worked, either approach would ultimately face the same issue. If we were to say that a high MI value (or equivalently a low K-S statistic) indicated that the two distributions they compared were ‘similar,’ then it would have to be said that this operator is not transitive. Therefore, finding a way to group together many IDs was non-trivial and computationally expensive. If the ‘similarity’ of these distributions was represented as a directed graph, clustering the distributions would require a graph exploration algorithm to find all groups of IDs that should be joined, possibly a clique-finding algorithm.

For the scope of this project, we instead arrived at much simpler approach, simple clustering. We decided to represent each ID’s SnapWeight distribution by its quantile values with q=20, resulting in a matrix of N IDs and 21 features of each ID. We applied K-Means clustering to these data for several K before then attempting the regression methods listed below.

Linear Regresson of Logit-Transformed SnapWeights

As noted earlier, SnapWeights range between 0 and 1, therefore to increase the validity of using a linear regression we used a logit function to project the values on to the real line. These values were then used as the response variable in a linear regression using the basic Ordinary Least Squares method to calculate parameters. Different combinations of the explanatory variables, Speed and Heading, were used.

As an initial indicator of the predictive power of each regression model, R-Squared values were examined and filtered for. This was applied to both data sets of individual IDs (i.e. a different linear model for each ID) as well as to data sets clustered by the distribution of their SnapWeights as mentioned in section above.

Afterwards, regressions that resulted in R-Squared values over .7 were recreated to store their calculated coefficients. These were then validated using our validation data to check for their true predictive power as measured by their L2 error. Then Tested? This sequence was done both for all IDs individually, as well as for clustered IDs. Results

As mentioned, the aperiodicity of the response data, found by applying a Fourier Transform, in addition to the high orders of the AR and MA models revealed that such models were not good fits to the data. As such these models were not applied to the validation or test data.

For our linear regression models, the response data used from our training set was chosen in different ways to fit different assumptions. The first assumption was that of across-the-board IID responses. The predictive power — as told by R-squared values — of such linear regressions that model SnapWeight, sampled from the entire training set irrespective of ID, was very low across varying sample sizes. Moving down the ladder of aggregation, regressions performed on data clustered by the distribution of SnapWeights (see section [ number]), R-Squared values were similarly low, barely a few hundredths over 0. As for individual IDs, only a handful out of thousands returned R-Squared values that were over 0.6. In addition, these IDs with higher R-Squared values were also found to be high in our Beta Regression experiment, indicating that there is likely some coincidentally convenient linear structure. Some abridged results are tabulated below.

Needless to say, it can be surmised that there is very low probability of correctly predicting SnapWeights based on Speed, Heading, Acceleration or any combination of them. Nevertheless, we used the relatively higher R-squared models, both from ID-respecting and ID-ignoring datasets, on our out-of- sample test data and compared the results using L1 error.

Regression Formula Individual ID R2 K-Means Large Sample R2 Large Sample L1 Clustered R2 Error SnapWeight ~ Speedx10 0.7802386 0.6087373 0.085790426907731 0.162566173902637 SnapWeight ~ Speedx10 0.886326 0.886326 0.085822108251274 0.162565246203703 + Headingx10 SnapWeight ~ 0.003093156 0.8562661 0.04310464 0.162306342793896 Acceleration * Headingx10 Figure 4 Max R-Squared Values