Physics 129 Fall 2010 D. Budker
Homework # 1; due Thursday, Sept. 9 Reading: Chapters 1,2 of Griffiths, Wikipedia.
1. This problem illustrates some typical and rather instructive estimates that working physicists cover their lunch-time napkins with. (a) Estimate the number of atoms contained in the Earth. (b) The angular momentum of an atom or a molecule, if it is nonzero, is on the order of . Estimate the angular momentum of the Earth’s rotation per atom in the units of .
2. What is the physical meaning of the Planck mass and Planck length scale? Derive analytical expressions for these quantities, and obtain approximate numerical values in grams, eV/c2, and centimeters.
3. Griffiths, Prob. 1.1. Consider first the case of a nonrelativistic particle. Does the answer change if the particle is relativistic?
4. Griffiths, Prob. 1.2 and 1.3.
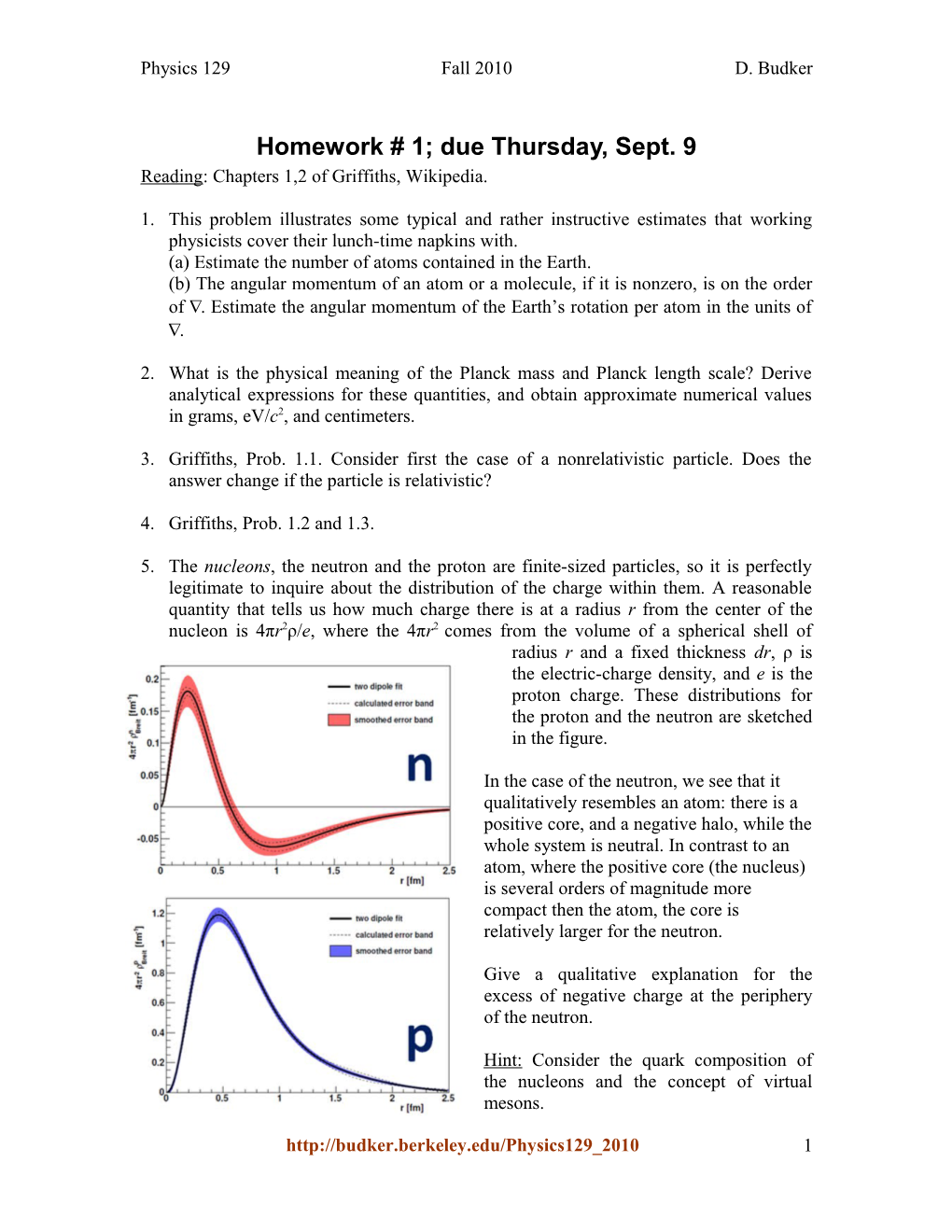
5. The nucleons, the neutron and the proton are finite-sized particles, so it is perfectly legitimate to inquire about the distribution of the charge within them. A reasonable quantity that tells us how much charge there is at a radius r from the center of the nucleon is 4πr2ρ/e, where the 4πr2 comes from the volume of a spherical shell of radius r and a fixed thickness dr, ρ is the electric-charge density, and e is the proton charge. These distributions for the proton and the neutron are sketched in the figure.
In the case of the neutron, we see that it qualitatively resembles an atom: there is a positive core, and a negative halo, while the whole system is neutral. In contrast to an atom, where the positive core (the nucleus) is several orders of magnitude more compact then the atom, the core is relatively larger for the neutron.
Give a qualitative explanation for the excess of negative charge at the periphery of the neutron.
Hint: Consider the quark composition of the nucleons and the concept of virtual mesons.
http://budker.berkeley.edu/Physics129_2010 1 Physics 129 Fall 2010 D. Budker
Homework # 2; due Thursday, Sept. 16 Reading: Chapters 2,3 of Griffiths, Wikipedia.
6. Positronium (Ps) is an atom that consists of an electron and its anti-particle a positron. (a) What can you say about the energy-level structure of positronium? Specifically, discuss the similarities and differences with the case of hydrogen. (b) Since both electron and positron are spin-1/2 particles, the total spin of positronium can be either S = 0 (para-positronium) or S = 1 (ortho-positronium). Which of these has lower ground-state energy, ortho- or para-positronium? (c) Both ground-state ortho- and para-positronium can decay via annihilation of their constituents. However, it turns out that the lifetimes of these two states differ by three orders of magnitude. Shorter-lived para-positronium annihilates emitting two photons, but this process is forbidden for ortho-positronium, so when it annihilates, three photons are emitted. Here we will be concerned with two-photon annihilation of para-positronium. Give an order-of-magnitude estimate of para-positronium lifetime, which is determined by this process. Hint: Use dimensional analysis and the fact that an amplitude of a process where a photon couples to an electron or a positron should be proportional to the coupling constant of the electromagnetic interaction, i.e., to the magnitude of the electron (positron) charge, e.
7. Griffiths, Problem 1.19
8. a) Griffiths, Problem 2.1. b) Now, also roughly (i.e., within 5 orders of magnitude) estimate the number of particles in the Universe. This can be done, for example, by assuming that the total energy (total mass plus the gravitational energy) of the Universe is zero, and dividing the total mass obtained from this by the mass of a proton. For this estimate, use the fact that the age of the Universe is some 13 billion years. c) Compare the two numbers. Dirac thought that the relation between these numbers is not an accident, which came to be known as the Dirac large-number hypothesis. Explain how temporal variation of fundamental “constants” follows from such a hypothesis, and estimate, to within several orders of magnitude, the relative variation of constants per year. d) Do a quick search to see if such variation is consistent with observations.
9. Griffiths, Problems 2.2 and 2.6
10. Griffiths, Problem 2.7
http://budker.berkeley.edu/Physics129_2010 2 Physics 129 Fall 2010 D. Budker
Homework # 3; due Thursday, Sept. 23 Reading: Chapters 3,4 of Griffiths, Wikipedia.
11. Griffiths, Problems 3.3, 3.4, 3.6, 3.21, 3.27
12. Using the simplest case of one spatial and one time dimension, show that Lorentz transformations are equivalent to hyperbolic rotations. What is the difference between a “normal” rotation of the xt frame and the hyperbolic rotation?
13. What are the particles that collide at LHC? What is the collision energy in the center of mass? Suppose that one were to build a fixed-target experiment to produce the same center-of-mass energy. What should the energy of the moving particle be? Is this possible in a man-made accelerator on Earth? In addition to the numerical results, please derive a formula that relates the center-of mass energy with the energy of the moving particle in a fixed target experiment assuming that the stationary and the moving particles have the same rest mass.
http://budker.berkeley.edu/Physics129_2010 3 Physics 129 Fall 2010 D. Budker
Homework # 4; due Thursday, Sept. 30 Reading: Chapter 4 of Griffiths
14. In lecture, it was mentioned that it is known that the electron is a point particle down to the size scale of 10-18 cm. Now, your friend is a middle-school science teacher who has never taken particle physics. Please explain to her how this is consistent with the center-of mass energy of modern colliders.
15. It is tempting to come up with a classical model for the spin of the electron. Consider on such (doomed) attempt, where the angular momentum of the electron is associated with the angular momentum of the electromagnetic field of the electron (the Coulomb field due to the charge, and the magnetic moment). Estimate the size of the electron that would follow from such a picture. For reference, the angular momentum associated with the combination of electric and magnetic fields is:
16. Review the derivation of the intrinsic parity of the negative pion presented in class. Use similar arguments to figure out the intrinsic parity of the neutral pion from the experimental result that the reaction d + π - n + n + π 0 does not occur.
17. Griffiths’ problem 4.36
18. Look up the rest-mass difference and the difference in lifetime between the two kinds of neutral kaons, KL and KS. Convert the mass difference into angular-frequency units (s-1), and, using the lifetimes, calculate the decay-rate difference in the same units. Compare these two quantities. Is the result surprising?
http://budker.berkeley.edu/Physics129_2010 4 Physics 129 Fall 2010 D. Budker
Homework # 5; due Thursday, October 7
Reading: Chapter 4 of Griffiths
19. A neutral kaon K0 is prepared at time t=0. What is the probability of finding this particle in the form of K0 at some later time t assuming that the particle is free? The other state we can find the particle in is K0-bar. What is the probability of this as a function of time? Neglect CP violation. Write analytical expressions in terms of the
mass difference m between KL and Ks and the respective decay rates of these particles. Plot the probabilities using the specific values from Problem 18 (or look them up).
20. Discuss the analogy between the neutral kaon system and the Zel’dovich bi-frequency pendulum, see figure below. Explain which physical quantities correspond to each other in these systems. Is the analogy complete?
21. Parity nonconservation due to the neutral weak interaction manifests itself in atomic transitions. For example, for the highly forbidden one-photon decay of unpolarized excited hydrogen
the emitted photons have a preferred circular polarization. The effect is larger for deuterium, due to its larger weak charge. For deuterium, the degree of circular polarization of the photons is 2∙10-4. As it turns out, while P-invariance is violated, the symmetry is almost restored by performing the combined transformation of spatial inversion and charge conjugation, C (this transformation changes matter into antimatter). So far, the only examples of CP-violation have been found in the decays of neutral K- and B-mesons, and for the purpose of this problem, we will assume that CP is a good symmetry.
The question is: if hydrogen preferentially emits right-circularly polarized (R) photons, what is the sign of the preferred circular polarization for antihydrogen?
http://budker.berkeley.edu/Physics129_2010 5 Physics 129 Fall 2010 D. Budker
Homework # 6; due Thursday, October 14 Reading: Chapters 4 and 6 of Griffiths
22. A theorem attributed to C. N. Yang and L. D. Landau states that a vector particle (i.e., a particle with intrinsic angular momentum J=1) cannot decay into two photons. Prove the theorem based on the most general considerations of the quantum field theory (QFT). This sounds scary, but is really rather simple, and goes like this.
The probability of the decay is proportional to the square of the amplitude of the decay process. This amplitude, in turn, has to be proportional to the first power of some quantity describing each of the particles participating in the process. For each of the photons, this quantity is conveniently chosen to be the polarization vector and 1 2 , respectively. Further, we can argue that some sort of polarization vector V (with three independent spatial components) can be employed to represent the initial vector particle in the decay amplitude. Finally, there is one more vector in the problem, k k k , representing the wave vectors (momenta) of the outgoing photons (in the 1 2 rest frame of the decaying particle, most natural for this problem, k1 k2 ). All that is left for us to do is to build all possible scalar or pseudoscalar expressions, where each of the polarization vectors would enter once, and there are no a-priori restrictions on how many times the momentum may enter into the expression. (Some of these combinations will be zero on the account of the transversality of photons.)
Please do this, and show that each of the possible expressions for the amplitude is odd under the exchange of the two photons. Explain why such amplitudes have to be zero in the framework of conventional QFT, and comment on how this can be used to test this framework. For extra credit: dig up some experimental upper limit on the branching ratios of the Landau-Yang forbidden decays.
23. (Corrected) a. In lecture, we have discussed the amplitude corresponding to the decay of para-positronium into two photons. Write out the rotational invariant for such decay. Are there any symmetries violated by such a decay? b. Which symmetries would be violated in the two-photon decay of the ortho- positronium?
24. Look up the luminosity achieved most recently (perhaps, today) at a major collider of your choice. Compare this to the design specification for this machine. Which process is used to measure/monitor the luminosity?
http://budker.berkeley.edu/Physics129_2010 6 Physics 129 Fall 2010 D. Budker
Homework # 7; due Thursday, October 21
Reading: Chapters 6 and 7 of Griffiths, Internet
25. Ultracold neutrons (UCN) have kinetic energies on the order of 10-7 eV. a. What is the order of magnitude of the temperature of UCN (in K)? b. What is the order of magnitude of the DeBroglie wavelength of a UCN? How does it compare with interatomic distances in condensed matter? c. Compare the kinetic energy of a UCN with the magnetic energy of the neutron inside a magnetized medium (in fully magnetized medium, magnetic induction is typically on the order of B = 1 T = 104 G). Comment on how one can use this to make polarizers for UCN beams. d. Calculate the change in the potential energy of a neutron when it moves vertically by 1 m in the Earth gravitational field. Compare this value with the kinetic energy of UCN. Comment on the role of gravity in UCN experiments.
26. Using the explicit form of the Dirac matrices, show that the anti-commutator of two such matrices γμ and γ is a unit 44 matrix times 2gμ, where gμ is the Minkowski metric. See the Section 7.1 in Griffiths.
27. You receive a call from a Swiss lawyer with a desperate plea for urgent expert help. (She has heard of you as an outstanding physicist presently studying elementary- particle physics, and, since the professors she had tried to contact never responded, you are her only hope.) CERN is (once again) being sued by anti-nuclear activists on the basis of the fact that the collision energy accessible to LHC is higher than has ever been possible with previous colliders. Thus, new particles can, in principle, be produced. The lawsuit is based on theories that a black hole may be produced, which will trigger catastrophic end of the Earth. You are asked to comment on whether such outcome is plausible, but there is only time for a quick assessment of facts. (Say, 15 minutes on internet.) Please draft a brief (but responsible) reply.
http://budker.berkeley.edu/Physics129_2010 7 Physics 129 Fall 2010 D. Budker
Homework # 8; due Thursday, November 4
Reading: Chapter 7 of Griffiths (plus you may need to review earlier material)
28. Find rotational invariants corresponding to the following processes: a. Natural optical activity: rotation of the direction of the polarization of linearly polarized light propagating in an isotropic medium. b. Faraday rotation: rotation of the direction of the polarization of linearly polarized light propagating in an isotropic medium in the presence of a static magnetic field collinear with the light-propagation direction. c. Same as in (b) but with magnetic field replaced with an electric field. Examine the properties of each of these invariants with respect to spatial inversion (P) and time reversal (T). Are any of these processes allowed if both parity and time-reversal invariance are good symmetries (i.e., neglecting the weak interactions)?
29. Explain why the nucleus containing one proton and one neutron (the deuteron) is stable, but there is no dineutron---the bound state of two neutrons. Hint: Assume that the strong-interaction forces are the same for a proton and a neutron (isospin invariance), and make use of the fact that there is only one bound state for the proton- neutron system (the deuteron), and it is spin-one, mostly coming from the addition of the proton's and neutron's spins. (There is, in fact, a small admixture of the orbital angular momentum L=1, but we can neglect it here.)
30. Consider photon scattering on a tau lepton.
a. Draw the Feynman diagrams for the process. b. Follow the QED rules summarized in Section 7.5 of Griffiths and write out the full expression for the total amplitude of the process. c. Explain why this process is legitimately described by QED (and not, for example, by QCD). d. Examine your expression for the amplitude. What are the dimensions (units) of the amplitude? (You may need to read around in Griffiths to see how the spinors are normalized, etc.) e. Find (by browsing Ch. 7) the appropriate expression for the differential cross- section of the scattering in terms of the amplitude. Verify that substituting the amplitude with the units you obtained in (c), you get the expected units for the cross-section.
http://budker.berkeley.edu/Physics129_2010 8 Physics 129 Fall 2010 D. Budker
Homework # 9; due Thursday, November 11 Reading: Chapters 6,7, and 9 of Griffiths
31. Paul Dirac was bothered by the question: why is that the position and momentum of a particle seem to be continuous, but the charge appears to be quantized. He was also bothered by the apparent asymmetry of the Maxwell equations due to the absence of magnetic monopoles. He considered the consequences of a possible existence of a magnetic monopole and derived a relation between the electric charge of the electron, -e, and the magnetic charge of the monopole, g. You will derive this relation in this problem.
Consider a non-relativistic electron scattering form a stationary and very heavy monopole. We first work in the classical-physics approximation. Assume that the impact parameter is b, and that the trajectory, to the lowest approximation, is just a straight line. a. Calculate the magnetic field acting on the electron as a function of time. b. Calculate the corresponding Lorentz force. What is the direction of this force? c. Calculate the angular momentum transferred to the electron in the course of the scattering. We now bring in Quantum Mechanics (QM). d. According to QM, orbital angular momentum is “quantized in units of .” Write down this quantization condition. This is the famous Dirac relation.
It is sometimes said that the quantization of the electrical charge follows from the existence of just a single magnetic monopole somewhere in the Universe. What you have just derived equips you for pondering this assertion…
32. What is the relation between the differential cross section d/ d and the total cross- section in the case of isotropic scattering? (Isotropic scattering is when the differential cross-section does not depend on either of the angles or .) Give an example of a process where scattering is isotropic. What is the intuitive physical reason for the isotropy in this case? Hint: examples of isotropic scattering can be found in Ch. 7 or 9.
33. Electromagnetic interactions of an atomic electron with the nucleus may be represented by a Feynman diagram corresponding to the exchange of a virtual photon between the electron and the nucleus. The weak-neutral-current interaction between the electron and the nucleus is represented by a similar diagram where the virtual photon is replaced by a virtual Z boson. Based on this fact, make a rough order-of- magnitude estimate of the energy shift (in eV) of the ground state of atomic hydrogen associated with the existence of the weak-neutral-current interaction. Note: the energy shift discussed in this problem is associated with the parity conserving part of the neutral-current weak interaction.
http://budker.berkeley.edu/Physics129_2010 9 Physics 129 Fall 2010 D. Budker
Homework # 10; due Wednesday, November 24 Reading: Chapter 9 of Griffiths; you might need to browse through Ch. 8 (that we skipped) as well
34. Starting from the formula for the lifetime of the muon [Eq. (9.35) in Griffiths] and the value of the muon lifetime (2.2 μs), estimate the lifetime of the tau lepton. How does one need to modify Eq. (9.35) so it is appropriate for the tau lepton? The masses of 2 2 the leptons are mμ 106 MeV/c ; mτ 1777 MeV/c . Compare the result of the estimate with the experimental value of the tau-lepton lifetime of 291 fs. Hint: no explicit calculations (beyond elementary) are needed here, but one has to consider what is different in the case of tau in addition to just the heavier mass.
35. a. Draw the Feynman diagram for the processes e+e- μ+μ-. Assuming we are in the center-of-mass frame, how does the corresponding cross-section scale with energy? (Assume that the energy is in the 1 GeV< 36. Your friend working at LBNL tells you at lunch that there is an exciting proposal in the works for a new collider for particle physics. Naturally, you want to ask her about some of the details. Think of a list of, say, 5-7 parameters of the proposed machine you would want to ask her about. After you make the list, look up these parameters for LHC, RHIC, Tevatron, LEP, and SLC. http://budker.berkeley.edu/Physics129_2010 10 Physics 129 Fall 2010 D. Budker 37. Estimate the size of a parity violation effect in a generic atom a. Compare diagrams with γ and Z b. First-order mixing c. E1/M1 d. Enhancements (close levels, Z3) 38. Explain why PNC mixing comes with an i. Connection to the 1st order Stark effect and EDM. 39. Estimate the orders of magnitude of the width and mass difference for neutral kaons. http://budker.berkeley.edu/Physics129_2010 11