Notes #30: Properties of Parallelograms (Section 6.2)

1 Geometry Notes: Chapter 6 Notes #30: Properties of Parallelograms (Section 6.2)

Both pairs of opposite sides of a parallelogram are ______(Definition of a Parallelogram) Parallelograms are shown; solve for the variables: ______angles are congruent 1.)

y 20 ______angles are congruent 30

______(consecutive) angles are supplementary x

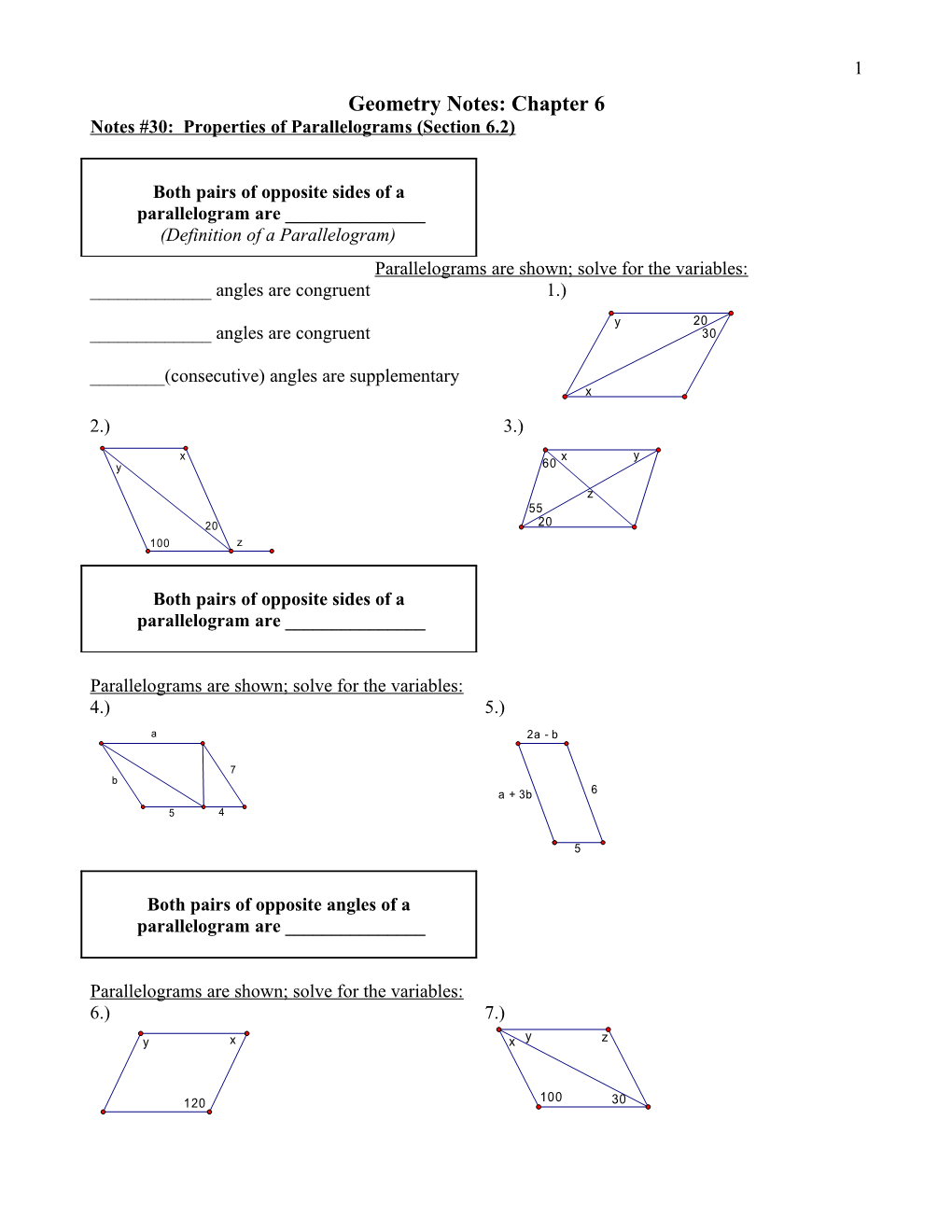
2.) 3.)

x x y y 60

z 55 20 20 100 z

Both pairs of opposite sides of a parallelogram are ______

Parallelograms are shown; solve for the variables: 4.) 5.) a 2a - b

7 b a + 3b 6 5 4

Both pairs of opposite angles of a parallelogram are ______

Parallelograms are shown; solve for the variables: 6.) 7.)

y x x y z

120 100 30 2

Diagonals of a parallelogram ______

Parallelograms are shown; solve for the variables: 8.) 9.)

a + 4 9 6 7

2b - 1 8 a b

For #10-11, draw a diagram, define your variable, write an equation, and solve. 10.) The perimeter of YABCD is 62in. 11.) In YWXYZ one angle is 8 times the size of AB is 5in longer than BC. Find the lengths another. Find the measures of the angles. of all four sides of the parallelogram.

If a transversal is cut into @ segments by parallel lines, then all transversals will be cut into @ segments by these parallel lines.

12.) If AB = 4, then BC = ____ and AD = ____ A E

B F 13.) If DC = 2x -1 and AC = 8x – 6, then x = ___ C G

(Problems #12 – 14) 14.) If EF = 5, FG = x + y, GH = 3y – 2x then x = ____ and y = ____. 3 Algebra Review: Simplifying, Multiplying, and Dividing Radicals 15.) 72 16.) 3 72 17.) -4 250

5 18.) 2 12 19.) 3 5 2 5 20.) 3

4 3 21.) 22.) 23.) (3 6 )2 5 8

Solving equations by factoring:  Write the equation in descending order and set = 0  Factor completely  Set each factor = 0  Solve for the variable. You should have the same number of solutions as the greatest exponent in the original equation

Solve each equation by factoring. List only Real solutions:

24.) 3x2 – 12 = 0 25.) 5x – 6 + x2 = 0 26.) 10x2 – 11x = -3

27.) 8x3 – 18x2 = -10x 28.) 6x3 – 2x = -x2 29.) x4 – 16 = 0 4 Notes #31: Parallelograms and Trapezoids (Sections 6.3 and 6.5)

You know that a quadrilateral IS A PARALLELOGRAM if and only if ONE or more of these conditions is met:

(I) Both pairs of opposite sides are (II) Both pairs of opposite angles parallel are congruent

(III) Both pairs of opposite sides are (IV) One pair of sides is both congruent congruent and parallel

(V) Diagonals bisect each other

Must ABCD be a parallelogram? If so, which of the above conditions was/were met?

1.) 2.) C 5 B B C

A 5 D A D

Yes or No? If yes, why? ______Yes or No? If yes, why? ______3.) 4.) B C B C 20 20

20 20 A D A D

Yes or No? If yes, why? ______Yes or No? If yes, why? ______5

5.) 6.) B C B C 60 120 60

A 60 A 60 D D

Yes or No? If yes, why? ______Yes or No? If yes, why? ______Find the values of a and b for which WXYZ must be a parallelogram

7.) WP = 3a, PY = b, XP = 2b – 7, PZ = b + 2 8.) WX = 3a – 3, YZ = a + 1, X Y m� X+ b �40, m Y b

W Z W Z

Trapezoids (Section 6.5)

A. Trapezoids: Trapezoids are quadrilaterals with ______pair of parallel sides (called ______) and one pair of non-parallel sides (called ______)

Question: Are trapezoids parallelograms?______Are trapezoids quadrilaterals?______

The median of a trapezoid:  Connects the ______of the legs  Is parallel to the ______ Is equal to the average lengths of the ______

base+ base median = 2 6 A trapezoid and its median are shown. Solve for x : (plug x back in to check!) 9.) 10.) 11.) 7

3x + 1 x 2x - 4 10 x - 3 5x - 2

19 4x + 1

Isosceles Trapezoids are trapezoids with ______.

The base angles of an isosceles The diagonals of an isosceles trapezoid are congruent trapezoid are congruent.

Complete the following problems: 12.) WXYZ is an isosceles trapezoid and 13.) ABCD is an isosceles trapezoid and m� W 70° . Find the measures of the m� B 102° . Find the measures of the remaining remaining three angles. three angles.

X Y B C

W Z A D

14.) If XZ = 2a + 7 and YW = 4a – 9, solve for a X Y

7 Algebra Practice: Solving equations by square rooting  Get x2 alone  Square root both sides of the equation. Use so that you have TWO solutions. Solve: 15.) x2 + 32 = 52 16.) (2x)2 + 82 = 102 17.) x2 + (5 3 )2 = 102

18.) x2 + x2 = 82 19.) x2 + (2x)2 = 152 20.) x2 + ( 4 6 )2 = (6 3 )2

Writing Equations of Lines:  Find slope Formula OR Parallel Lines OR Perpendicular Lines

 Solve for b by plugging m, x, y into y = mx + b  Plug m and b back into y = mx + b  Convert to standard form if necessary.

Find the equation of the line… 23.) that goes through the points (-5, 4) and 24.) that is parallel to: y = 5x – 11 and that passes (3, 0) in Standard Form. through the point (6, 3) in slope-intercept form. 8 Notes #32 : Special Quadrilaterals (Sections 6.1 and 6.4) Quadrilaterals

Trapezoids Parallelograms

Rectangle Rhombus Isosceles Trapezoid

Square

Quadrilaterals

Parallelograms

Rectangles Rhombi

Trapezoids

Squares 9

Name all quadrilaterals that fit the description: (P = parallelogram, T = trapezoid, Re = rectangle, Rh = rhombus, S = square)

1.) both pairs of opposite sides are congruent 2.) all sides are congruent

3.) diagonals bisect each other 4.) both pairs of adjacent sides are congruent

5.) diagonals are congruent 6.) all angles are congruent

7.) both pairs of opposite sides are parallel 8.) exactly one pair of sides is parallel

ABCD is a rhombus: B 3 4 9.) If m�1 40° , find the measures of the other angles.

A 2 C 1 5 10.) If m�5- 3 x 9 , solve for x

11.) If m�1+ 2 x � 1, m - 2 5 x 8 . Find x. 12.) If m�1- 7 x � 3, m + 3 2 x 12 , find x.

PQRS is a rectangle: Q R ° 4 13.) If m�1行 23 , find m 2, m 3, m 4 O

3 1 P 2 S

14.) If PO = 5x – 1 and QS = 38, solve for x. 15.) PQ is two inches shorter than QR. The perimeter of PQRS is 40 inches. Find the length of each side. 10 Algebra Review: Reducing fractions and fractions with radicals

-6 18 -5 20 16.) 17.) 2 2

4 20 -8 27 18.) 19.) 4 2

2 2 20.) -9� ( - 5) (4)(2)(3) 21.) -9� (6) - 4( - 3)( 3) 4 4

22.) Find the equation of the line with an 23.) Find the equation of the line perpendicular to x-intercept of -5 and a y-intercept of 4 in slope- the line: y = 5x – 1 and passing through the point intercept form. (-2, 3) in standard form. 11 Notes #33 : Quadrilaterals in the Coordinate Plane (Sections 6.6 and 6.7)

A. Graphing Special Quadrilaterals on the Coordinate Plane Graph points A, B, and C of the given special quadrilateral. Find the coordinates of D.

1.) Rectangle ABCD: 2.) Square ABCD: A (-5, 3) B(-5, 7) C(4, 7) D(___, ___) A (-4, 0) B(0, 4) C(4, 0) D(___, ___) y y 10 10 9 9 8 8 7 7 6 6 5 5 4 4 3 3 2 2 1 1 x x -10 -9 -8 -7 -6 -5 -4 -3 -2 -1 1 2 3 4 5 6 7 8 9 10 -10 -9 -8 -7 -6 -5 -4 -3 -2 -1 1 2 3 4 5 6 7 8 9 10 -1 -1 -2 -2 -3 -3 -4 -4 -5 -5 -6 -6 -7 -7 -8 -8 -9 -9 -10 -10 3.) Isosceles trapezoid ABCD: 4.) Parallelogram ABCD: A (-6, -3) B(-4, 4) C(4, 4) D(___, ____) A (-7, -5) B(-4, 0) C(-1, 0) D(___, ____) y y 10 10 9 9 8 8 7 7 6 6 5 5 4 4 3 3 2 2 1 1 x x -10 -9 -8 -7 -6 -5 -4 -3 -2 -1 1 2 3 4 5 6 7 8 9 10 -10 -9 -8 -7 -6 -5 -4 -3 -2 -1 1 2 3 4 5 6 7 8 9 10 -1 -1 -2 -2 -3 -3 -4 -4 -5 -5 -6 -6 -7 -7 -8 -8 -9 -9 -10 -10

Points on the same horizontal line have the same _____- coordinate

Points on the same vertical line have the same _____- coordinate

For #5-8, give the coordinates of points W and Z without using any new variables. 5.) rectangle 6.) parallelogram y

(b, c) W

O x x (0, 0) (a, 0) 12 7.) rhombus 8.) isosceles trapezoid y y

(0, b) (-b, c) W Z

W x x O (a, 0) (-m, 0) O (m, 0)

B. Proofs in the Coordinate Plane When we place a quadrilateral in the coordinate plane, we have some flexibility in how we name the vertices. In general, though, it is a good idea to name vertices as expressions that are divisible by ______in case we need to use the midpoint formula.

Formulas that we need to know when working with the coordinate plane

Slope =

Distance =

Midpoint =

9.) Complete a plan to prove the following:

The segment connecting the midpoints of the legs y R (2b, 2c) of a trapezoid is parallel to the bases of the A (2d, 2c) trapezoid. M N Given: TRAP is a trapezoid, T M is the midpoint of RT P (2a, 0) x N is the midpoint of AP

Prove: MNP TP, MN P RA

Place the trapezoid in the coordinate plane with a vertex at the (a) ______and a side along the

(b) ______. Since midpoints will be involved, name coordinates using multiples of (c) ______.

To show that line are parallel, check for equal (d) ______by using the formula for (f) ______. 13

10.) Now use coordinate Geometry to complete the proof of #9 above. y R (2b, 2c) Given: TRAP is a trapezoid, A (2d, 2c) M is the midpoint of RT M N N is the midpoint of AP T x Prove: MNP TP, MN P RA P (2a, 0) a) Find the coordinates of M and N. How do the multiples of 2 help?

Reminder: midpoint = (______, ______)

M is the midpoint of RT : R(____, ____) T(____, ____)

N is the midpoint of _____: (____, ____) (____, ____)

b) Find and compare the slopes of MN, TP , and RA Reminder: slope = ______

MN : M(___, ___) N(___, ___) TP : T(___, ___) P(___, ___) RA : R(___, ___) A(___,___)

c) What can you conclude and why?

14 11.) Consider Quadrilateral WXYZ. Prove that the quadrilateral formed when connecting the midpoints of the sides of WXYZ is always a parallelogram. y a) Which formulas will we need to use here X (2d, 2e) and why?

Y (2b, 2c)

W (0, 0) b) Draw quadrilateral QRST that connects the x midpoints of the sides of WXYZ, respectively. Z (2a, 0) c.) Find the coordinates of Q, R, S, T d.) Prove that QRST is a parallelogram (show that the opposite sides of QRST are ______Q is the mdpt of WX : W(___, ___) X(___, ___) using the ______formula)

QR : Q(___, ___) R(___, ___)

R is the mdpt of ____: (___, ___) (___, ___)

RS : R(___, ___) S(___, ___) S is the mdpt of ____: (___, ___) (___, ___)

: (___, ___) (___, ___) T is the mdpt of ____: (___, ___) (___, ___) ST

TQ : (___, ___) (___, ___)

15 y 12.) Complete the plan for the coordinate proof: N (2a, 2b) M (0, 2b) W Given: MNOP is a rectangle T, W, V, U are midpoints of its sides T V

x U P (2a, 0) Prove: TWVU is a rhombus

Place the rectangle in the coordinate plane with a vertex at the (a) ______and a side along the (b) ______. Since midpoints will be involved, name coordinates using multiples of (c) ______. Since a rhombus is a parallelogram with (d) ______, show that (e) _____@ _____ @ _____ @ _____ using the (f) ______Formula.

13.) Now use coordinate Geometry to complete the proof for #12 above. y W N (2a, 2b) Given: MNOP is a rectangle M (0, 2b) T, W, V, U are midpoints of its sides T V

x Prove: TWVU is a rhombus U P (2a, 0) a) Find the coordinates of T, W, V, and U using the ______formula. T is the midpoint of _____ W is the midpoint of ______

V is the midpoint of ______U is the midpoint of ______

b) Find and compare TU, UV, VW, and WT using the ______formula.

TU: T(____, ____) U(____, ____) UV: U(____, ____) V(____, ____)

VW: V(____, ____) W(____, ____) WT: W(____, ____) T(____, ____) 16

17 Geometry Chapter 6 Study Guide Name: ______Per: ______

For #1, answer the question about parallelograms.

1.) Opposite sides of a parallelogram are both (a)______and (b)______. Opposite angles of a parallelogram are (c) ______and consecutive angles of a parallelogram are (d) ______. Diagonals of a parallelogram (e) ______.

For #2-5, PQRS is a parallelogram. Find the values of a, b, x, and y. 2. 3. 2. a =______R Q Q a R b =______80 y b y x =______a 10 b y =______

S 20 x 45 x P P S 3. a =______4 C 6 b =______x =______y =______

5. 4. 4. a =______R Q 2x + 3y R Q b =______a x 50 64 a b 7 x =______y =______y 5x + 4y 9 32 5 100 20 P S 5. a =______28 b =______b P 5 S x =______y =______

For #6, draw a picture, write an equation, and solve. 6. Quadrilateral ABCD is a parallelogram. The length of AB is five more than 6. AB=______three times the length of BC . The perimeter of ABCD is 58m. Find the length BC=______of each side. CD=______DA=______18

For #7 – 10, study each figure and decide whether ABCD must be a parallelogram. If the answer is yes, explain the rule you used. 7. If yes, why? 8. If yes, why?

C B B 12 C 62 80

8 8 80 62 D A D A 12

9. If yes, why? 10. If yes, why?

C B C B

6 4 A D A D

For #11 - 12, simplify the radical expressions: 11.) 12.) 11. 2 a) 6 98 a) (4 3) (a) ______(b) ______(c) ______骣 b) 3 12 5 15 2 3 ( )( ) b) 琪 12. 桫3 6 (a) ______

骣7 (b) ______c) 琪 2 桫 2 骣2 3 (c) ______c) 琪桫4 2

13. AW, BX , CY and DZ are parallel. WX = XY = YZ a.) If AD = 27, CD = ______13. A W (a) ______b.) If AC = 5x – 8 and AB = x + 5, then B X x = ______(b) ______C Y (c) ______D Z c.) If BC = 7x and AD = 9x + 24, then x = ______19 Classify each as true or false: 14. ______14. Opposite sides of a rectangle must be parallel. 15. ______15. The diagonals of a rhombus must be perpendicular. 16. ______16. Same side interior angles of a parallelogram are complementary. 17. ______17. Diagonals of a rectangle bisect corner angles. 18. ______18. The diagonals of a square bisect each other.

Write the letter of every special quadrilateral that has the given property. A Parallelogram B Rectangle C Rhombus 19. ______D Square E Trapezoid 20. ______

19. All sides congruent. 20. Diagonals bisect corner angles. 21. ______

22. ______21. Opposite sides congruent. 22. Diagonals are congruent. 23. ______23. Diagonals are perpendicular. 24. Exactly one pair of parallel sides. 24. ______

GRIP is a rectangle. Complete: G R 25. If m�1 20 , then find m行2, m 3, and m 4 4 25. ______

26. If GI = 16, find RS and RP S 3 26. ______2 P 1 I

27. ______27. If PS = 6x – 4 and GI = 28, then x = _____

ABCD is a rhombus. Complete: B 28. If AB = 8, find BC, CD, and DA 3 4 28. ______C A 2 m 1 20 m行2, m 3, and m 4 29. If � , then find 1 29. ______

D 30. If m�1- 5 x � 3 and m + 3 3 x 5, solve for x. 30. ______20

Trapezoids and their medians are shown. Solve for x. 31. 32.

3x + 2 31. ______

2x + 1 11 5x 2x + 4

32. ______2x + 1

For #33-36, solve for x by factoring: 33. 12x2 = 20x 34. 6x2 – 6 = -16x 33. ______

34. ______

35. 8x2 – 9 + 6x = 0 36. 9x3 + 18x2 – 72x = 0 35. ______

36. ______

For #37-38, solve for x 2 2 38.) (2x)2 + 52 = 132 37. ______37.) x2 + (2 3) = (2 7 )

38. ______

For #39-40, simplify: -12 45 2 39. ______39.) 40.) -6� (8) - 4(3)( 3) 6 4

40. ______21 Graph points A, B, and C of the given special quadrilateral. Find the coordinates of D. 41.) Trapezoid ABCD: 42.) Parallelogram ABCD: A (-3, 1) B(-6, 4) C(6, 4) D(___, ___) A (2, 0) B(-8, 0) C(-4, 7) D(___, ___) y y 10 10 9 9 8 8 7 7 6 6 5 5 4 4 3 3 2 2 1 1 x x -10 -9 -8 -7 -6 -5 -4 -3 -2 -1 1 2 3 4 5 6 7 8 9 10 -10 -9 -8 -7 -6 -5 -4 -3 -2 -1 1 2 3 4 5 6 7 8 9 10 -1 -1 -2 -2 -3 -3 -4 -4 -5 -5 -6 -6 -7 -7 -8 -8 -9 -9 -10 -10 Give coordinates for points D and S without using any new variables. 43.) parallelogram 44.) rhombus

y y D (c + a, b)

(0, d)

D x O S (c, 0) O x (c, 0) S

45.) Complete the plan for the coordinate proof y for the following theorem:

The diagonals of a parallelogram bisect each B (2b, 2c) C (2a + 2b, 2c) other.

E Given: ABCD is a parallelogram

A Prove: AC bisects BD , and BD bisects AC x D (2a, 0)

Place the parallelogram in the coordinate plane with a vertex at the (a) ______and a side along the (b) ______. Since midpoints will be involved, name coordinates using multiples of (c) ______. To show that the segments bisect each other, show that the midpoints have the same (d)______. 22

46.) Now use coordinate Geometry to complete the proof for #45 above.

Given: ABCD is a parallelogram B (2b, 2c) C (2a + 2b, 2c)

Prove: AC bisects BD , and BD bisects AC A x D (2a, 0) a) Find the coordinates of the midpoint of AC . How do the multiples of 2 help?

b) Find the coordinates of the midpoint of BD . How do the multiples of 2 help?