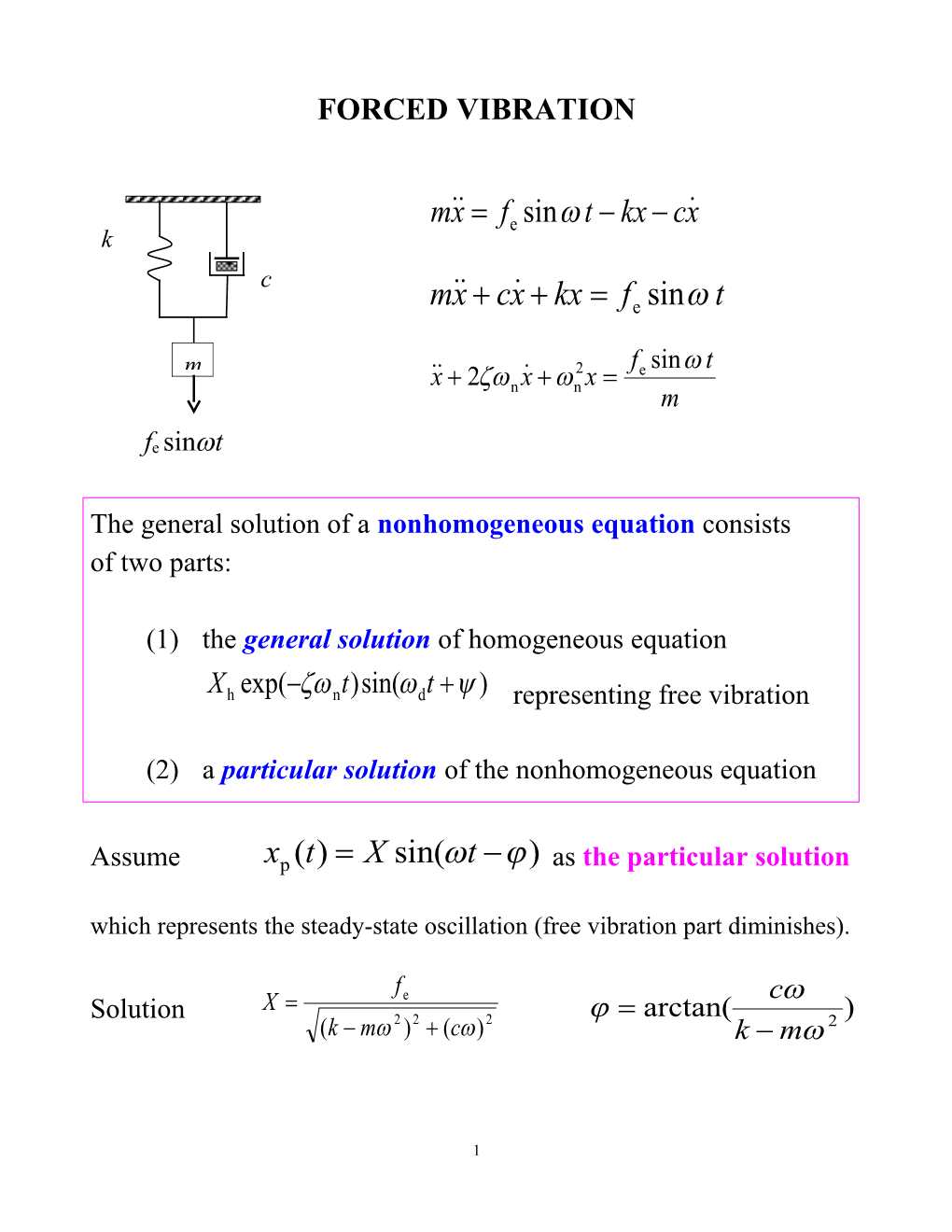
FORCED VIBRATION
m˙x˙ fe sin t kx cx˙ k c m˙x˙ cx˙ kx fe sin t
m 2 f sin t ˙x˙ 2 x˙ x e n n m
fe sint
The general solution of a nonhomogeneous equation consists of two parts:
(1) the general solution of homogeneous equation
X h exp(nt)sin(dt ) representing free vibration
(2) a particular solution of the nonhomogeneous equation
Assume xp (t) X sin(t ) as the particular solution which represents the steady-state oscillation (free vibration part diminishes).
f e c Solution X arctan( ) (k m 2 ) 2 (c) 2 k m 2
1 free 3 particular 2
1
0 0 4 8 12 -1
-2
-3
Solution of homogenous equation (free vibration)
Particular solution of nonhomogenous solution
3 forced
2
1
0 0 4 8 12 -1
-2
-3
Complete solution (forced vibration) x(t) xh (t) xp (t)
2 c k kX 1 2 f arctan[ n ] e [1 ( )2 ]2 [2 ( )]2 1 ( )2 n n n kX/fe 10
8
6 4 2
0 /n nn 0 1 2 3 4 180
90
/n nn 0 0 1 2 3 4
3 kX These formulas indicate that the nondimensional amplitude and fe phase depend on the frequency ratio . n
The curves can be divided into three regions: (1) 1 (smaller than and not close to 1) ; (2) 1; and (3) ℏ 1. n n n
In the region of close to 1, the nondimensional amplitude n becomes very large.
kX 1 1 at fe 2 n
Damping has a great influence at resonance. If damping is absent, the amplitude becomes infinite at resonance in theory.
kX Where dose the maximum occur ( )? What is the maximum? fe n
Beyond 2 , the nondimensional amplitude is smaller than n one, that is, the amplitude is smaller than the static deflection.
The other thing to notice is that the response x(t) lags behind the ° ° excitation force by a phase angle 90 for n and 90 for n . At n , there is a steep change of phase angle.
The natural frequency n (internal) and (external) should not be confused. 4 Machines with Rotating Parts
Suppose the center of mass is away from the e centre of rotation. The off-centred mass will create an unbalanced force of me 2 cost in horizontal direction me 2 sint in vertical direction
(Complex) Frequency Response Function (information only)
The excitation can be a sinusoidal or co-sinusoidal function of time. Both cases can be represented by a single function of time.
m˙x˙ cx˙ kx fe exp(i t) (i 1 )
The steady-state solution is assumed as x(t) X exp(it)
2 (k ic m )X exp(it) fe exp(i t)
f f X e x(t) e exp(it) k ic m 2 k ic m 2
The frequency response function is defined as X 1 2 f e k ic m
5 Support Motion and Vibration Isolation
Sometimes a vibration is initiated by an oscillatory motion, from ground (earthquake) or an adjacent connection, rather than by an oscillatory force. Theses cases can be considered as support motion.
Equation of motion x m m˙x˙ k(x y) c(x˙ y˙ ) k c let z x y y m˙z˙ cz˙ kz m˙y˙ y(t) Y exp(it)
Suppose z(t) Z exp[i(t )] and x(t) X exp[i(t )]. Z and , and X and can be found from the above equation.
2 2 2 X k (c) 1[2 ( /n )] 2 2 2 2 2 2 Y (k m ) (c) [1 ( /n ) ] [2 ( /n )]
3 2 ( /n ) tan 2 2 1 ( /n ) [2 ( /n )]
6 18 0 10 X/Y 12 0 8
6 0 Series1
0 Series2 6 0 1 2 3 4 5 Series3 Series4 4 Series5 Series6 2
0 / n 0 1 2 2 3 4
X From the above graph of , one can see for good isolation, k must be Y X selected such that 2 (then 1). Such a device is called a Y n vibration isolator.
7 Transfer Function
When the excitation is a harmonic function of time, it is easy to find the response. For a general excitation of f (t) , determining the response in the time-domain can be difficult.
The equation of motion of a mass-spring-damper system under a general excitation is m˙x˙ cx˙ kx f (t)
Taking the Laplace transform and assuming the initial response is zero, yields
1 X (s) G(s)F(s) G(s) ms 2 cs k and
X (s) G(s) transfer function. F(s)
It can be noticed that G(i) is the frequency response function defined in a previous section.
Once the excitation f (t) is given in a known system, F(s) can be found and X (s) can also be found from the system’s transfer function. By means of the inverse Laplace transform of X (s) , the system’s response to f (t) , x(t) can be determined.
Example:
8 Suppose the excitation to a mass-spring-damper system is shown below
f(t)
f 0
t
a
f exp(sa) F(s) f (t)exp(st)dt f exp(st)dt 0 1. 0 0 a s
1 2. G(s) ms 2 cs k
f exp(sa) 3. X (s) G(s)F(s) 0 s(ms2 cs k)
1 -1 f exp(sa) 4. x(t) L [X (s)] L [ 0 ] H (t a)u(t a) s(ms2 cs k) where H is a unit step function and u is the response of a unit step function.
9