IB Math Studies – Chapter 3 – Sets and Venn Diagrams – Review Questions
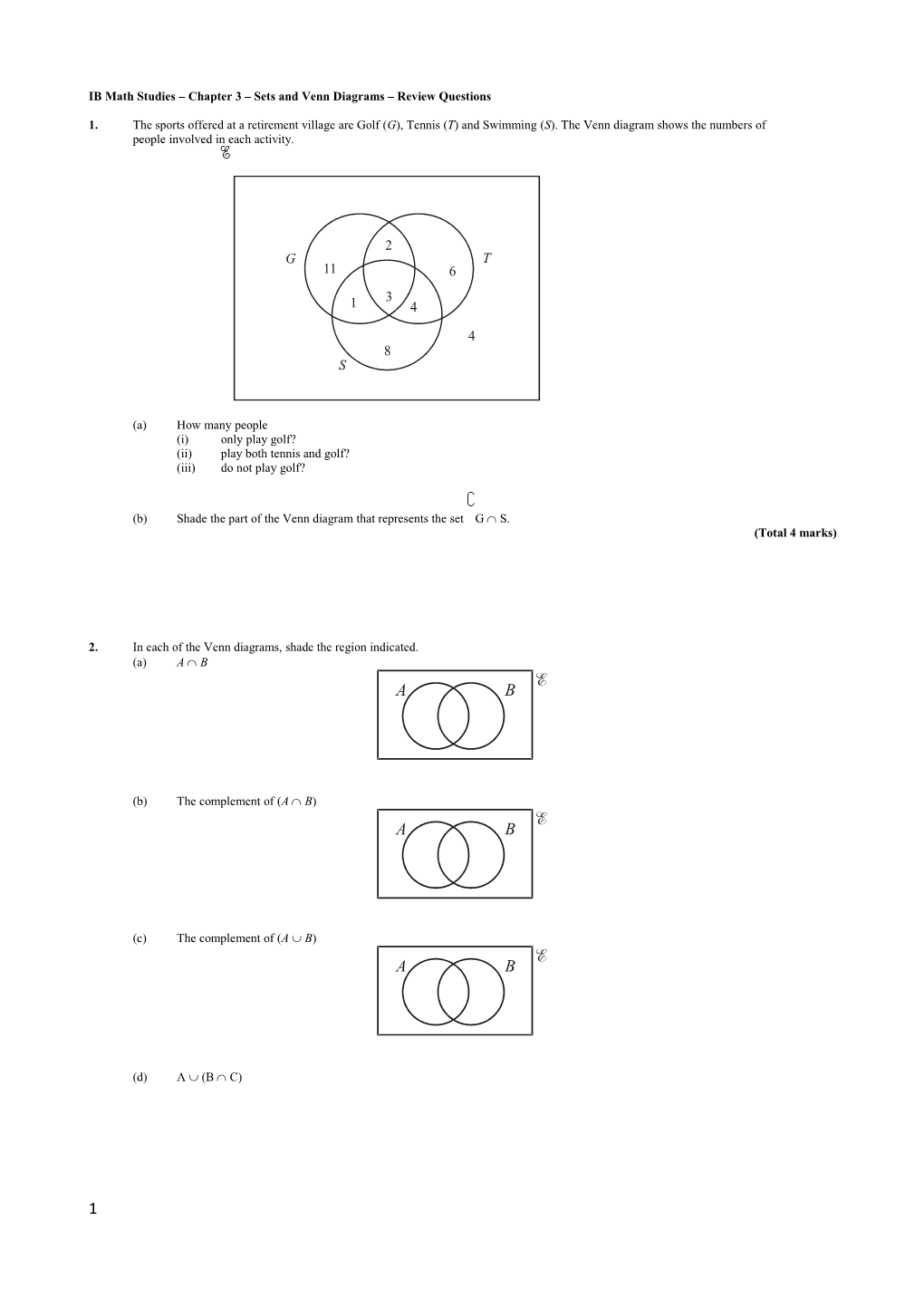
1. The sports offered at a retirement village are Golf (G), Tennis (T) and Swimming (S). The Venn diagram shows the numbers of people involved in each activity.
2 G T 11 6 3 1 4
4 8 S
(a) How many people (i) only play golf? (ii) play both tennis and golf? (iii) do not play golf?
(b) Shade the part of the Venn diagram that represents the set G S. (Total 4 marks)
2. In each of the Venn diagrams, shade the region indicated. (a) A B A B
(b) The complement of (A B) A B
(c) The complement of (A B) A B
(d) A (B C)
1 A B
C
(Total 4 marks)
3. Let
= {positive integers less than 15}; X= {multiples of 2}; Y = {multiples of 3}.
(a) Show, in a Venn diagram, the relationship between the sets , X and Y. (1) (b) List the elements of: (i) X Y (1)
(ii) X Y. (2) (c) Find the number of elements in the complement of (X Y). (2) (Total 6 marks)
4. A group of 30 children are surveyed to find out which of the three sports cricket (C), basketball (B) or volleyball (V) they play. The results are as follows: 3 children do not play any of these sports 2 children play all three sports 6 play volleyball and basketball 3 play cricket and basketball 6 play cricket and volleyball 16 play basketball 12 play volleyball. (a) Draw a Venn diagram to illustrate the relationship between the three sports played. (1)
(b) On your Venn diagram indicate the number of children that belong to each region. (3)
(c) How many children play only cricket? (2) (Total 6 marks)
5. The universal set U is defined as the set of positive integers less than 10. The subsets A and B are defined as: A = {integers that are multiples of 3} B = {integers that are factors of 30} (a) List the elements of (i) A; (ii) B.
(b) Place the elements of A and B in the appropriate region in the Venn diagram below.
2 U
A B
(Total 4 marks)
6. A committee U has three sub-committees: research R, finance F and purchasing P. No member belongs to both finance and purchasing sub-committees. Some members belong to both research and purchasing committees. All members of the finance sub- committee also belong to the research sub-committee. Draw a Venn diagram, showing the relationship between the sets U, R, F and P. (Total 4 marks)
7. (a) Shade (A B) C′ on the diagram below. U A B C
(2) (b) In the Venn diagram below, the number of elements in each region is given. Find n ((P Q) R).
U P 2 3 1 Q
6
4 5
9
R
(2)
+ (c) U is the set of positive integers, . E is the set of even numbers. M is the set of multiples of 3. (i) List the first six elements of the set M. (ii) List the first six elements of the set E′ M. (2)
(Total 6 marks)
8. At a certain school there are 90 students studying for their IB diploma. They are required to study at least one of the subjects: Physics, Biology or Chemistry. 50 students are studying Physics, 60 students are studying Biology, 55 students are studying Chemistry, 3 30 students are studying both Physics and Biology, 10 students are studying both Biology and Chemistry but not Physics, 20 students are studying all three subjects. Let x represent the number of students who study both Physics and Chemistry but not Biology. Then 25–x is the number who study Chemistry only. The figure below shows some of this information and can be used for working. U with n(U) 90
Physics x Chemistry 25–x 20 10
Biology 20
(a) Express the number of students who study Physics only, in terms of x. (b) Find x. (c) Determine the number of students studying at least two of the subjects.
(Total 6 marks) Mark Scheme
1. (a) (i) 11 (A1) (C1) (ii) 2 + 3 = 5
(A1)
(C1) (iii) 8 + 4 + 6 + 4 = 22
(A1)
(C1)
(b)
G T
S
(A1)
(C1) [4]
2. (a) A B
(A1)
4 ε A B
(b) The complement of (A B)
(A1) ε A B
(c) The complement of (A B)
(A1) ε A B
(d) A (B C)
(A1) ε A B
C
[4]
3. (a) X Y
(A1)
1
Note: Award (Al) for a diagram correctly labelled with X, Y and .
(b) (i) (X Y) = {6, 12}
(A1)
(ii) X Y = {2, 4, 8, 10, 14}
(A2)
3 5
(c) (X Y) = (X Y) = {l, 5, 7, 11, 13}
(A1) n(X Y) = 5
(A1)
2 [6]
4. (a)
(A1) Award (A1) for a rectangle containing 3 intersecting circles. (b)
(A3)
4
C B 1 9 4 2 4
2 3 V
Notes: (b) Award (A3) for 6 or 7 correct numbers in the regions. (A2) for 4 or 5 correct, (A1) for 2 or 3 correct.
(c) 1 + 9 + 4 + 2 + 4 + 2 + 3 = 25
(M1) n(C) = 30 – 25 = 5
(A1) OR n(C) = 5
(C2)
2 [6]
5. (a) (i) A = {3, 6, 9} (A1) (C1) (ii) B = {1, 2, 3, 5, 6}
(A1)
(C1) Note: Candidates must list all the elements and no extra elements for each (A1)
(b) U A B 3 1, 2 9 6 5
(A2) 6 (C2) Notes: Follow through from (a). Award (A1) for 3 and 6 in the intersection. Award (A1) for other values correctly positioned [4]
6. U R P F
(A4) Note: Award (A1) for rectangle, (A1) for F entirely within R, (A1) for F disjoint from P, (A1) for P R non-empty. [4]
7. (a)
not shading C or shading A B (A1) correct shading (A1) (C2)
(b) Identifying the correct 5 numbers 3, 4, 5, 6, 9 (A1) 27 (A1) (C2)
(c) (i) M = {3, 6, 9, 12, 15, 18} brackets not required. (A1) (ii) E′ M = {3, 9, 15, 21, 27, 33} (ft) from (i). (A1)(ft) (C2) [6]
8. The full diagram is as follows, but need not be fully filled in.
(a) 50 – (30 + x) = 20 – x (M1) (A1) (C2) Notes: Award (C2) for either of these as final answer. Can award (M1) for 50 minus a sum of numbers intended to count the entries in all the 7 Physics intersections. Also award (M1)(A0) if the sign is distributed incorrectly, giving answers such as 50 – 30 + x or 20 + x.
(b) 60 + x + (20 – x) + (25 – x) = 90 (M1) (M1) Note: Award (M1) for 90 seen on one side of the equation, (M1) for a reasonable attempt to order the entries. Therefore x = 15. (A1) (ft) (C3)
(c) Number studying at least two subjects is 55. (A1) (ft) (C1) Note: Allow correct (ft) with no marking shown [6]
8