QQPLOT Statement
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

The Statistical Analysis of Distributions, Percentile Rank Classes and Top-Cited
How to analyse percentile impact data meaningfully in bibliometrics: The statistical analysis of distributions, percentile rank classes and top-cited papers Lutz Bornmann Division for Science and Innovation Studies, Administrative Headquarters of the Max Planck Society, Hofgartenstraße 8, 80539 Munich, Germany; [email protected]. 1 Abstract According to current research in bibliometrics, percentiles (or percentile rank classes) are the most suitable method for normalising the citation counts of individual publications in terms of the subject area, the document type and the publication year. Up to now, bibliometric research has concerned itself primarily with the calculation of percentiles. This study suggests how percentiles can be analysed meaningfully for an evaluation study. Publication sets from four universities are compared with each other to provide sample data. These suggestions take into account on the one hand the distribution of percentiles over the publications in the sets (here: universities) and on the other hand concentrate on the range of publications with the highest citation impact – that is, the range which is usually of most interest in the evaluation of scientific performance. Key words percentiles; research evaluation; institutional comparisons; percentile rank classes; top-cited papers 2 1 Introduction According to current research in bibliometrics, percentiles (or percentile rank classes) are the most suitable method for normalising the citation counts of individual publications in terms of the subject area, the document type and the publication year (Bornmann, de Moya Anegón, & Leydesdorff, 2012; Bornmann, Mutz, Marx, Schier, & Daniel, 2011; Leydesdorff, Bornmann, Mutz, & Opthof, 2011). Until today, it has been customary in evaluative bibliometrics to use the arithmetic mean value to normalize citation data (Waltman, van Eck, van Leeuwen, Visser, & van Raan, 2011). -

A Logistic Regression Equation for Estimating the Probability of a Stream in Vermont Having Intermittent Flow
Prepared in cooperation with the Vermont Center for Geographic Information A Logistic Regression Equation for Estimating the Probability of a Stream in Vermont Having Intermittent Flow Scientific Investigations Report 2006–5217 U.S. Department of the Interior U.S. Geological Survey A Logistic Regression Equation for Estimating the Probability of a Stream in Vermont Having Intermittent Flow By Scott A. Olson and Michael C. Brouillette Prepared in cooperation with the Vermont Center for Geographic Information Scientific Investigations Report 2006–5217 U.S. Department of the Interior U.S. Geological Survey U.S. Department of the Interior DIRK KEMPTHORNE, Secretary U.S. Geological Survey P. Patrick Leahy, Acting Director U.S. Geological Survey, Reston, Virginia: 2006 For product and ordering information: World Wide Web: http://www.usgs.gov/pubprod Telephone: 1-888-ASK-USGS For more information on the USGS--the Federal source for science about the Earth, its natural and living resources, natural hazards, and the environment: World Wide Web: http://www.usgs.gov Telephone: 1-888-ASK-USGS Any use of trade, product, or firm names is for descriptive purposes only and does not imply endorsement by the U.S. Government. Although this report is in the public domain, permission must be secured from the individual copyright owners to reproduce any copyrighted materials contained within this report. Suggested citation: Olson, S.A., and Brouillette, M.C., 2006, A logistic regression equation for estimating the probability of a stream in Vermont having intermittent -

Integration of Grid Maps in Merged Environments
Integration of grid maps in merged environments Tanja Wernle1, Torgeir Waaga*1, Maria Mørreaunet*1, Alessandro Treves1,2, May‐Britt Moser1 and Edvard I. Moser1 1Kavli Institute for Systems Neuroscience and Centre for Neural Computation, Norwegian University of Science and Technology, Trondheim, Norway; 2SISSA – Cognitive Neuroscience, via Bonomea 265, 34136 Trieste, Italy * Equal contribution Corresponding author: Tanja Wernle [email protected]; Edvard I. Moser, [email protected] Manuscript length: 5719 words, 6 figures,9 supplemental figures. 1 Abstract (150 words) Natural environments are represented by local maps of grid cells and place cells that are stitched together. How transitions between map fragments are generated is unknown. Here we recorded grid cells while rats were trained in two rectangular compartments A and B (each 1 m x 2 m) separated by a wall. Once distinct grid maps were established in each environment, we removed the partition and allowed the rat to explore the merged environment (2 m x 2 m). The grid patterns were largely retained along the distal walls of the box. Nearer the former partition line, individual grid fields changed location, resulting almost immediately in local spatial periodicity and continuity between the two original maps. Grid cells belonging to the same grid module retained phase relationships during the transformation. Thus, when environments are merged, grid fields reorganize rapidly to establish spatial periodicity in the area where the environments meet. Introduction Self‐location is dynamically represented in multiple functionally dedicated cell types1,2 . One of these is the grid cells of the medial entorhinal cortex (MEC)3. The multiple spatial firing fields of a grid cell tile the environment in a periodic hexagonal pattern, independently of the speed and direction of a moving animal. -

How to Use MGMA Compensation Data: an MGMA Research & Analysis Report | JUNE 2016
How to Use MGMA Compensation Data: An MGMA Research & Analysis Report | JUNE 2016 1 ©MGMA. All rights reserved. Compensation is about alignment with our philosophy and strategy. When someone complains that they aren’t earning enough, we use the surveys to highlight factors that influence compensation. Greg Pawson, CPA, CMA, CMPE, chief financial officer, Women’s Healthcare Associates, LLC, Portland, Ore. 2 ©MGMA. All rights reserved. Understanding how to utilize benchmarking data can help improve operational efficiency and profits for medical practices. As we approach our 90th anniversary, it only seems fitting to celebrate MGMA survey data, the gold standard of the industry. For decades, MGMA has produced robust reports using the largest data sets in the industry to help practice leaders make informed business decisions. The MGMA DataDive® Provider Compensation 2016 remains the gold standard for compensation data. The purpose of this research and analysis report is to educate the reader on how to best use MGMA compensation data and includes: • Basic statistical terms and definitions • Best practices • A practical guide to MGMA DataDive® • Other factors to consider • Compensation trends • Real-life examples When you know how to use MGMA’s provider compensation and production data, you will be able to: • Evaluate factors that affect compensation andset realistic goals • Determine alignment between medical provider performance and compensation • Determine the right mix of compensation, benefits, incentives and opportunities to offer new physicians and nonphysician providers • Ensure that your recruitment packages keep pace with the market • Understand the effects thatteaching and research have on academic faculty compensation and productivity • Estimate the potential effects of adding physicians and nonphysician providers • Support the determination of fair market value for professional services and assess compensation methods for compliance and regulatory purposes 3 ©MGMA. -
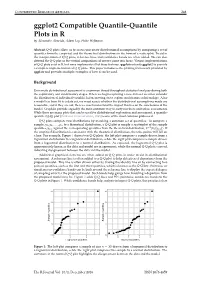
Ggplot2 Compatible Quantile-Quantile Plots in R by Alexandre Almeida, Adam Loy, Heike Hofmann
CONTRIBUTED RESEARCH ARTICLES 248 ggplot2 Compatible Quantile-Quantile Plots in R by Alexandre Almeida, Adam Loy, Heike Hofmann Abstract Q-Q plots allow us to assess univariate distributional assumptions by comparing a set of quantiles from the empirical and the theoretical distributions in the form of a scatterplot. To aid in the interpretation of Q-Q plots, reference lines and confidence bands are often added. We can also detrend the Q-Q plot so the vertical comparisons of interest come into focus. Various implementations of Q-Q plots exist in R, but none implements all of these features. qqplotr extends ggplot2 to provide a complete implementation of Q-Q plots. This paper introduces the plotting framework provided by qqplotr and provides multiple examples of how it can be used. Background Univariate distributional assessment is a common thread throughout statistical analyses during both the exploratory and confirmatory stages. When we begin exploring a new data set we often consider the distribution of individual variables before moving on to explore multivariate relationships. After a model has been fit to a data set, we must assess whether the distributional assumptions made are reasonable, and if they are not, then we must understand the impact this has on the conclusions of the model. Graphics provide arguably the most common way to carry out these univariate assessments. While there are many plots that can be used for distributional exploration and assessment, a quantile- quantile (Q-Q) plot (Wilk and Gnanadesikan, 1968) is one of the most common plots used. Q-Q plots compare two distributions by matching a common set of quantiles. -
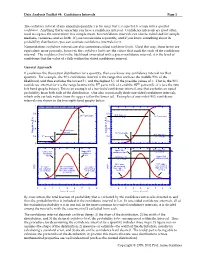
Data Analysis Toolkit #4: Confidence Intervals Page 1 Copyright © 1995
Data Analysis Toolkit #4: Confidence Intervals Page 1 The confidence interval of any uncertain quantity x is the range that x is expected to occupy with a specified confidence. Anything that is uncertain can have a confidence interval. Confidence intervals are most often used to express the uncertainty in a sample mean, but confidence intervals can also be calculated for sample medians, variances, and so forth. If you can calculate a quantity, and if you know something about its probability distribution, you can estimate confidence intervals for it. Nomenclature: confidence intervals are also sometimes called confidence limits. Used this way, these terms are equivalent; more precisely, however, the confidence limits are the values that mark the ends of the confidence interval. The confidence level is the likelihood associated with a given confidence interval; it is the level of confidence that the value of x falls within the stated confidence interval. General Approach If you know the theoretical distribution for a quantity, then you know any confidence interval for that quantity. For example, the 90% confidence interval is the range that encloses the middle 90% of the likelihood, and thus excludes the lowest 5% and the highest 5% of the possible values of x. That is, the 90% confidence interval for x is the range between the 5th percentile of x and the 95th percentile of x (see the two left-hand graphs below). This is an example of a two-tailed confidence interval, one that excludes an equal probability from both tails of the distribution. One also occasionally finds one-sided confidence intervals, which only exclude values from the upper tail or the lower tail. -

Control Chart Based on the Mann-Whitney Statistic
IMS Collections Beyond Parametrics in Interdisciplinary Research: Festschrift in Honor of Professor Pranab K. Sen Vol. 1 (2008) 156–172 c Institute of Mathematical Statistics, 2008 DOI: 10.1214/193940307000000112 A nonparametric control chart based on the Mann-Whitney statistic Subhabrata Chakraborti1 and Mark A. van de Wiel2 University of Alabama and Vrije Universiteit Amsterdam Abstract: Nonparametric or distribution-free charts can be useful in statisti- cal process control problems when there is limited or lack of knowledge about the underlying process distribution. In this paper, a phase II Shewhart-type chart is considered for location, based on reference data from phase I analysis and the well-known Mann-Whitney statistic. Control limits are computed us- ing Lugannani-Rice-saddlepoint, Edgeworth, and other approximations along with Monte Carlo estimation. The derivations take account of estimation and the dependence from the use of a reference sample. An illustrative numeri- cal example is presented. The in-control performance of the proposed chart is shown to be much superior to the classical Shewhart X¯ chart. Further com- parisons on the basis of some percentiles of the out-of-control conditional run length distribution and the unconditional out-of-control ARL show that the proposed chart is almost as good as the Shewhart X¯ chart for the normal distribution, but is more powerful for a heavy-tailed distribution such as the Laplace, or for a skewed distribution such as the Gamma. Interactive soft- ware, enabling a complete implementation of the chart, is made available on a website. 1. Introduction Control charts are most widely used in statistical process control (SPC) to detect changes in a production process. -

JMASM25: Computing Percentiles of Skew-Normal Distributions," Journal of Modern Applied Statistical Methods: Vol
Journal of Modern Applied Statistical Methods Volume 5 | Issue 2 Article 31 11-1-2005 JMASM25: Computing Percentiles of Skew- Normal Distributions Sikha Bagui The University of West Florida, Pensacola, [email protected] Subhash Bagui The University of West Florida, Pensacola, [email protected] Follow this and additional works at: http://digitalcommons.wayne.edu/jmasm Part of the Applied Statistics Commons, Social and Behavioral Sciences Commons, and the Statistical Theory Commons Recommended Citation Bagui, Sikha and Bagui, Subhash (2005) "JMASM25: Computing Percentiles of Skew-Normal Distributions," Journal of Modern Applied Statistical Methods: Vol. 5 : Iss. 2 , Article 31. DOI: 10.22237/jmasm/1162355400 Available at: http://digitalcommons.wayne.edu/jmasm/vol5/iss2/31 This Algorithms and Code is brought to you for free and open access by the Open Access Journals at DigitalCommons@WayneState. It has been accepted for inclusion in Journal of Modern Applied Statistical Methods by an authorized editor of DigitalCommons@WayneState. Journal of Modern Applied Statistical Methods Copyright © 2006 JMASM, Inc. November, 2006, Vol. 5, No. 2, 575-588 1538 – 9472/06/$95.00 JMASM25: Computing Percentiles of Skew-Normal Distributions Sikha Bagui Subhash Bagui The University of West Florida An algorithm and code is provided for computing percentiles of skew-normal distributions with parameter λ using Monte Carlo methods. A critical values table was created for various parameter values of λ at various probability levels of α . The table will be useful to practitioners as it is not available in the literature. Key words: Skew normal distribution, critical values, visual basic. Introduction distribution, and for λ < 0 , one gets the negatively skewed distribution. -

Guidance for Comparing Background and Chemical Concentrations in Soil for CERCLA Sites
EPA 540-R-01-003 OSWER 9285.7-41 September 2002 Guidance for Comparing Background and Chemical Concentrations in Soil for CERCLA Sites Office of Emergency and Remedial Response U.S. Environmental Protection Agency Washington, DC 20460 Page ii PREFACE This document provides guidance to the U.S. Environmental Protection Agency Regions concerning how the Agency intends to exercise its discretion in implementing one aspect of the CERCLA remedy selection process. The guidance is designed to implement national policy on these issues. Some of the statutory provisions described in this document contain legally binding requirements. However, this document does not substitute for those provisions or regulations, nor is it a regulation itself. Thus, it cannot impose legally binding requirements on EPA, States, or the regulated community, and may not apply to a particular situation based upon the circumstances. Any decisions regarding a particular remedy selection decision will be made based on the statute and regulations, and EPA decision makers retain the discretion to adopt approaches on a case-by-case basis that differ from this guidance where appropriate. EPA may change this guidance in the future. ACKNOWLEDGMENTS The EPA working group, chaired by Jayne Michaud (Office of Emergency and Remedial Response), included TomBloomfield (Region 9), Clarence Callahan (Region 9), Sherri Clark (Office of Emergency and Remedial Response), Steve Ells (Office of Emergency and Remedial Response), Audrey Galizia (Region 2), Cynthia Hanna (Region 1), Jennifer Hubbard (Region 3), Dawn Ioven (Region 3), Julius Nwosu (Region 10), Sophia Serda (Region 9), Ted Simon (Region 4), and Paul White (Office of Research and Development). -

4. Descriptive Statistics
4. Descriptive statistics Any time that you get a new data set to look at one of the first tasks that you have to do is find ways of summarising the data in a compact, easily understood fashion. This is what descriptive statistics (as opposed to inferential statistics) is all about. In fact, to many people the term “statistics” is synonymous with descriptive statistics. It is this topic that we’ll consider in this chapter, but before going into any details, let’s take a moment to get a sense of why we need descriptive statistics. To do this, let’s open the aflsmall_margins file and see what variables are stored in the file. In fact, there is just one variable here, afl.margins. We’ll focus a bit on this variable in this chapter, so I’d better tell you what it is. Unlike most of the data sets in this book, this is actually real data, relating to the Australian Football League (AFL).1 The afl.margins variable contains the winning margin (number of points) for all 176 home and away games played during the 2010 season. This output doesn’t make it easy to get a sense of what the data are actually saying. Just “looking at the data” isn’t a terribly effective way of understanding data. In order to get some idea about what the data are actually saying we need to calculate some descriptive statistics (this chapter) and draw some nice pictures (Chapter 5). Since the descriptive statistics are the easier of the two topics I’ll start with those, but nevertheless I’ll show you a histogram of the afl.margins data since it should help you get a sense of what the data we’re trying to describe actually look like, see Figure 4.2. -

Chapter 5: Spatial Autocorrelation Statistics
Chapter 5: Spatial Autocorrelation Statistics Ned Levine1 Ned Levine & Associates Houston, TX 1 The author would like to thank Dr. David Wong for help with the Getis-Ord >G= and local Getis-Ord statistics. Table of Contents Spatial Autocorrelation 5.1 Spatial Autocorrelation Statistics for Zonal Data 5.3 Indices of Spatial Autocorrelation 5.3 Assigning Point Data to Zones 5.3 Spatial Autocorrelation Statistics for Attribute Data 5.5 Moran=s “I” Statistic 5.5 Adjust for Small Distances 5.6 Testing the Significance of Moran’s “I” 5.7 Example: Testing Houston Burglaries with Moran’s “I” 5.8 Comparing Moran’s “I” for Two Distributions 5.10 Geary=s “C” Statistic 5.10 Adjusted “C” 5.13 Adjust for Small Distances 5.13 Testing the Significance of Geary’s “C” 5.14 Example: Testing Houston Burglaries with Geary’s “C” 5.14 Getis-Ord “G” Statistic 5.16 Testing the Significance of “G” 5.18 Simulating Confidence Intervals for “G” 5.20 Example: Testing Simulated Data with the Getis-Ord AG@ 5.20 Example: Testing Houston Burglaries with the Getis-Ord AG@ 5.25 Use and Limitations of the Getis-Ord AG@ 5.25 Moran Correlogram 5.26 Adjust for Small Distances 5.27 Simulation of Confidence Intervals 5.27 Example: Moran Correlogram of Baltimore County Vehicle Theft and Population 5.27 Uses and Limitations of the Moran Correlogram 5.30 Geary Correlogram 5.34 Adjust for Small Distances 5.34 Geary Correlogram Simulation of Confidence Intervals 5.34 Example: Geary Correlogram of Baltimore County Vehicle Thefts 5.34 Uses and Limitations of the Geary Correlogram 5.35 Table of Contents (continued) Getis-Ord Correlogram 5.35 Getis-Ord Simulation of Confidence Intervals 5.37 Example: Getis-Ord Correlogram of Baltimore County Vehicle Thefts 5.37 Uses and Limitations of the Getis-Ord Correlogram 5.39 Running the Spatial Autocorrelation Routines 5.39 Guidelines for Examining Spatial Autocorrelation 5.39 References 5.42 Attachments 5.44 A. -

Gaussian Copula Vs. Loans Loss Assessment: a Simplified and Easy-To-Use Model Viviane Y
Journal of Business Case Studies – September/October 2012 Volume 8, Number 5 Gaussian Copula Vs. Loans Loss Assessment: A Simplified And Easy-To-Use Model Viviane Y. Naïmy, Ph.D., Notre Dame University, Louaize, Lebanon ABSTRACT The copula theory is a fundamental instrument used in modeling multivariate distributions. It defines the joint distribution via the marginal distributions together with the dependence between variables. Copulas can also model dynamic structures. This paper offers a brief description of the copulas’ statistical procedures implemented on real market data. A direct application of the Gaussian copula to the assessment of a portfolio of loans belonging to one of the banks operating in Lebanon is illustrated in order to make the implementation of the copula simple and straightforward. Keywords: Gaussian Copula Theory; Modeling Multivariate Distributions; Loans Assessment INTRODUCTION he concept of “copulas1” was named by Sklar (1959). In statistics, the word copula describes the function that “joins” one dimensional distribution functions to form multivariate ones, and may serve to characterize several dependence concepts. It was initiated in the context of probabilistic metric Tspaces. Copulas function became a popular multivariate modeling tool in financial applications since 1999 (Embrechts, McNeil and Straumann (1999)). They are used for asset allocation, credit scoring, default risk modeling, derivative pricing, and risk management (Bouyè, Durrleman, Bikeghbali, Riboulet, and Roncalli 2000; Cherubini, Luciano, and Vecchiato 2004). They became more and more popular because as proven, the returns of financial assets are non-Gaussian and show nonlinearities; therefore, copulas became an imperative modeling device in a non-Gaussian world. They implement algorithms to simulate asset return distributions in a realistic way by modeling a multivariate dependence structure separately from the marginal distributions.