Exact Inference for Categorical Data
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Logrank Tests (Freedman)
PASS Sample Size Software NCSS.com Chapter 702 Logrank Tests (Freedman) Introduction This module allows the sample size and power of the logrank test to be analyzed under the assumption of proportional hazards. Time periods are not stated. Rather, it is assumed that enough time elapses to allow for a reasonable proportion of responses to occur. If you want to study the impact of accrual and follow-up time, you should use the one of the other logrank modules available in PASS. The formulas used in this module come from Machin et al. (2018). They are also given in Fayers and Machin (2016) where they are applied to sizing quality of life studies. They were originally published in Freedman (1982) and are often referred to by that name. A clinical trial is often employed to test the equality of survival distributions for two treatment groups. For example, a researcher might wish to determine if Beta-Blocker A enhances the survival of newly diagnosed myocardial infarction patients over that of the standard Beta-Blocker B. The question being considered is whether the pattern of survival is different. The two-sample t-test is not appropriate for two reasons. First, the data consist of the length of survival (time to failure), which is often highly skewed, so the usual normality assumption cannot be validated. Second, since the purpose of the treatment is to increase survival time, it is likely (and desirable) that some of the individuals in the study will survive longer than the planned duration of the study. The survival times of these individuals are then unobservable and are said to be censored. -

Overview-Of-Statistical-Analytics-And
Brief Overview of Statistical Analytics and Machine Learning tools for Data Scientists Tom Breur 17 January 2017 It is often said that Excel is the most commonly used analytics tool, and that is hard to argue with: it has a Billion users worldwide. Although not everybody thinks of Excel as a Data Science tool, it certainly is often used for “data discovery”, and can be used for many other tasks, too. There are two “old school” tools, SPSS and SAS, that were founded in 1968 and 1976 respectively. These products have been the hallmark of statistics. Both had early offerings of data mining suites (Clementine, now called IBM SPSS Modeler, and SAS Enterprise Miner) and both are still used widely in Data Science, today. They have evolved from a command line only interface, to more user-friendly graphic user interfaces. What they also share in common is that in the core SPSS and SAS are really COBOL dialects and are therefore characterized by row- based processing. That doesn’t make them inherently good or bad, but it is principally different from set-based operations that many other tools offer nowadays. Similar in functionality to the traditional leaders SAS and SPSS have been JMP and Statistica. Both remarkably user-friendly tools with broad data mining and machine learning capabilities. JMP is, and always has been, a fully owned daughter company of SAS, and only came to the fore when hardware became more powerful. Its initial “handicap” of storing all data in RAM was once a severe limitation, but since computers now have large enough internal memory for most data sets, its computational power and intuitive GUI hold their own. -
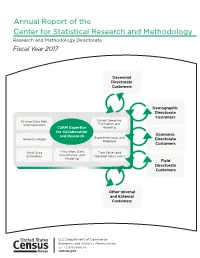
Annual Report of the Center for Statistical Research and Methodology Research and Methodology Directorate Fiscal Year 2017
Annual Report of the Center for Statistical Research and Methodology Research and Methodology Directorate Fiscal Year 2017 Decennial Directorate Customers Demographic Directorate Customers Missing Data, Edit, Survey Sampling: and Imputation Estimation and CSRM Expertise Modeling for Collaboration Economic and Research Experimentation and Record Linkage Directorate Modeling Customers Small Area Simulation, Data Time Series and Estimation Visualization, and Seasonal Adjustment Modeling Field Directorate Customers Other Internal and External Customers ince August 1, 1933— S “… As the major figures from the American Statistical Association (ASA), Social Science Research Council, and new Roosevelt academic advisors discussed the statistical needs of the nation in the spring of 1933, it became clear that the new programs—in particular the National Recovery Administration—would require substantial amounts of data and coordination among statistical programs. Thus in June of 1933, the ASA and the Social Science Research Council officially created the Committee on Government Statistics and Information Services (COGSIS) to serve the statistical needs of the Agriculture, Commerce, Labor, and Interior departments … COGSIS set … goals in the field of federal statistics … (It) wanted new statistical programs—for example, to measure unemployment and address the needs of the unemployed … (It) wanted a coordinating agency to oversee all statistical programs, and (it) wanted to see statistical research and experimentation organized within the federal government … In August 1933 Stuart A. Rice, President of the ASA and acting chair of COGSIS, … (became) assistant director of the (Census) Bureau. Joseph Hill (who had been at the Census Bureau since 1900 and who provided the concepts and early theory for what is now the methodology for apportioning the seats in the U.S. -

Fibrinogen Levels Are Associated with Lymph Node Involvement And
ANTICANCER RESEARCH 38 : 1097-1104 (2018) doi:10.21873/anticanres.12328 Fibrinogen Levels Are Associated with Lymph Node Involvement and Overall Survival in Gastric Cancer Patients JÚLIUS PALAJ 1, ŠTEFAN KEČKÉŠ 2, VÍTĚZSLAV MAREK 1, DANIEL DYTTERT 1, IVETA WACZULÍKOVÁ 3 and ŠTEFAN DURDÍK 1 1Department of Oncological Surgery, St. Elizabeth Cancer Institute, Slovak Republic and Faculty of Medicine in Bratislava of the Comenius University, Bratislava, Slovak Republic; 2Department of Immunodiagnostics, St. Elizabeth Cancer Institute, Bratislava, Slovak Republic; 3Department of Nuclear Physics and Biophysics, Comenius University, Faculty of Mathematics, Physics and Informatics, Bratislava, Slovak Republic Abstract. Background/Aim: Combination of perioperative accounting for 6.8% of all diagnosed cancers and making this chemotherapy with gastrectomy with D2 lymphadenectomy cancer the 5th most common malignancy globally (2). improves long-term survival in patients with gastric cancer. Moreover, it is the third leading cause of death in both sexes The aim of this study was to investigate the predictive value accounting for 8.8% of the total deaths from cancer (3). of preoperative levels of CRP, albumin, fibrinogen, In spite of advancements in chemotherapy and local neutrophil-to-lymphocyte ratio and routinely used tumor control of GC, prognosis remains poor, mainly because of markers (CEA, CA 19-9, CA 72-4) for lymph node the advancement of the disease at the time of diagnosis. involvement. Materials and Methods: This retrospective Approximately 50% patients in western countries have study was conducted in 136 patients who underwent surgery metastases at the time of diagnosis, and from those without between 2007 and 2015. Bivariable and multivariable metastatic disease only 50% are eligible for gastric resection analyses were performed in order to identify important (4). -

Towards a Fully Automated Extraction and Interpretation of Tabular Data Using Machine Learning
UPTEC F 19050 Examensarbete 30 hp August 2019 Towards a fully automated extraction and interpretation of tabular data using machine learning Per Hedbrant Per Hedbrant Master Thesis in Engineering Physics Department of Engineering Sciences Uppsala University Sweden Abstract Towards a fully automated extraction and interpretation of tabular data using machine learning Per Hedbrant Teknisk- naturvetenskaplig fakultet UTH-enheten Motivation A challenge for researchers at CBCS is the ability to efficiently manage the Besöksadress: different data formats that frequently are changed. Significant amount of time is Ångströmlaboratoriet Lägerhyddsvägen 1 spent on manual pre-processing, converting from one format to another. There are Hus 4, Plan 0 currently no solutions that uses pattern recognition to locate and automatically recognise data structures in a spreadsheet. Postadress: Box 536 751 21 Uppsala Problem Definition The desired solution is to build a self-learning Software as-a-Service (SaaS) for Telefon: automated recognition and loading of data stored in arbitrary formats. The aim of 018 – 471 30 03 this study is three-folded: A) Investigate if unsupervised machine learning Telefax: methods can be used to label different types of cells in spreadsheets. B) 018 – 471 30 00 Investigate if a hypothesis-generating algorithm can be used to label different types of cells in spreadsheets. C) Advise on choices of architecture and Hemsida: technologies for the SaaS solution. http://www.teknat.uu.se/student Method A pre-processing framework is built that can read and pre-process any type of spreadsheet into a feature matrix. Different datasets are read and clustered. An investigation on the usefulness of reducing the dimensionality is also done. -

An Example of Statistical Data Analysis Using the R Environment for Statistical Computing
Tutorial: An example of statistical data analysis using the R environment for statistical computing D G Rossiter Version 1.4; May 6, 2017 Subsoil vs. topsoil clay, by zone Regression Residuals vs. Fitted Values, subsoil clay % 128 80 15 138 ● 17119 137 1 ● 139 70 2 ● 3 10 ● 4 ● 60 ● ● 5 50 0 Slopes: Residual 40 zone 1 : 0.834 Subsoil clay % Subsoil clay ● ● zone 2 : 0.739 zone 3 : 0.564 −5 30 zone 4 : 1.081 overall: 0.829 −10 20 81 −15 10 145 10 20 30 40 50 60 70 80 20 30 40 50 60 70 Topsoil clay % Fitted GLS 2nd−order trend surface, subsoil clay % 340000 335000 330000 N 325000 320000 315000 660000 670000 680000 690000 700000 E Copyright © D G Rossiter 2008 { 2010, 2014, 2017 All rights reserved. Repro- duction and dissemination of the work as a whole (not parts) freely permitted if this original copyright notice is included. Sale or placement on a web site where payment must be made to access this document is strictly prohibited. To adapt or translate please contact the author ([email protected]). Contents 1 Introduction1 2 Example Data Set2 2.1 Loading the dataset...........................3 2.2 A normalized database structure*...................5 3 Research questions8 4 Univariarte Analysis9 4.1 Univariarte Exploratory Data Analysis................9 4.2 Point estimation; inference of the mean............... 14 4.3 Answers.................................. 15 5 Bivariate correlation and regression 16 5.1 Conceptual issues in correlation and regression........... 16 5.2 Bivariate Exploratory Data Analysis................. 18 5.3 Bivariate Correlation Analysis..................... 22 5.4 Fitting a regression line........................ -

Randomization-Based Test for Censored Outcomes: a New Look at the Logrank Test
Randomization-based Test for Censored Outcomes: A New Look at the Logrank Test Xinran Li and Dylan S. Small ∗ Abstract Two-sample tests have been one of the most classical topics in statistics with wide appli- cation even in cutting edge applications. There are at least two modes of inference used to justify the two-sample tests. One is usual superpopulation inference assuming the units are independent and identically distributed (i.i.d.) samples from some superpopulation; the other is finite population inference that relies on the random assignments of units into different groups. When randomization is actually implemented, the latter has the advantage of avoiding distribu- tional assumptions on the outcomes. In this paper, we will focus on finite population inference for censored outcomes, which has been less explored in the literature. Moreover, we allow the censoring time to depend on treatment assignment, under which exact permutation inference is unachievable. We find that, surprisingly, the usual logrank test can also be justified by ran- domization. Specifically, under a Bernoulli randomized experiment with non-informative i.i.d. censoring within each treatment arm, the logrank test is asymptotically valid for testing Fisher's null hypothesis of no treatment effect on any unit. Moreover, the asymptotic validity of the lo- grank test does not require any distributional assumption on the potential event times. We further extend the theory to the stratified logrank test, which is useful for randomized blocked designs and when censoring mechanisms vary across strata. In sum, the developed theory for the logrank test from finite population inference supplements its classical theory from usual superpopulation inference, and helps provide a broader justification for the logrank test. -

Using SPSS to Analyze Complex Survey Data: a Primer
Journal of Modern Applied Statistical Methods Volume 18 Issue 1 Article 16 4-6-2020 Using SPSS to Analyze Complex Survey Data: A Primer Danjie Zou University of British Columbia, [email protected] Jennifer E. V. Lloyd University of British Columbia, [email protected] Jennifer L. Baumbusch University of British Columbia, [email protected] Follow this and additional works at: https://digitalcommons.wayne.edu/jmasm Part of the Applied Statistics Commons, Social and Behavioral Sciences Commons, and the Statistical Theory Commons Recommended Citation Zou, D., Lloyd, J. E. V., & Baumbusch, J. L. (2019). Using SPSS to analyze complex survey data: A primer Journal of Modern Applied Statistical Methods, 18(1), eP3253. doi: 10.22237/jmasm/1556670300 This Regular Article is brought to you for free and open access by the Open Access Journals at DigitalCommons@WayneState. It has been accepted for inclusion in Journal of Modern Applied Statistical Methods by an authorized editor of DigitalCommons@WayneState. Using SPSS to Analyze Complex Survey Data: A Primer Cover Page Footnote Thank you to the McCreary Centre Society (https://www.mcs.bc.ca/), who collects and owns the British Columbia Adolescent Health Survey data. Thanks also to Dr. Colleen Poon, Allysha Ram, Dr. Elizabeth Saewyc, and Annie Smith for their guidance as we worked with the data. We also thank the Social Sciences and Humanities Research Council of Canada (SSHRC) for an Insight Development grant awarded to Dr. Baumbusch. Finally, thanks to blind reviewers for their comments that improved the paper. An SPSS syntax file with the commands outlined in this paper is va ailable for download at: http://blogs.ubc.ca/jenniferlloyd/ This regular article is available in Journal of Modern Applied Statistical Methods: https://digitalcommons.wayne.edu/ jmasm/vol18/iss1/16 Journal of Modern Applied Statistical Methods May 2019, Vol. -

Survival Analysis Using a 5‐Step Stratified Testing and Amalgamation
Received: 13 March 2020 Revised: 25 June 2020 Accepted: 24 August 2020 DOI: 10.1002/sim.8750 RESEARCH ARTICLE Survival analysis using a 5-step stratified testing and amalgamation routine (5-STAR) in randomized clinical trials Devan V. Mehrotra Rachel Marceau West Biostatistics and Research Decision Sciences, Merck & Co., Inc., North Wales, Randomized clinical trials are often designed to assess whether a test treatment Pennsylvania, USA prolongs survival relative to a control treatment. Increased patient heterogene- ity, while desirable for generalizability of results, can weaken the ability of Correspondence Devan V. Mehrotra, Biostatistics and common statistical approaches to detect treatment differences, potentially ham- Research Decision Sciences, Merck & Co., pering the regulatory approval of safe and efficacious therapies. A novel solution Inc.,NorthWales,PA,USA. Email: [email protected] to this problem is proposed. A list of baseline covariates that have the poten- tial to be prognostic for survival under either treatment is pre-specified in the analysis plan. At the analysis stage, using all observed survival times but blinded to patient-level treatment assignment, “noise” covariates are removed with elastic net Cox regression. The shortened covariate list is used by a condi- tional inference tree algorithm to segment the heterogeneous trial population into subpopulations of prognostically homogeneous patients (risk strata). After patient-level treatment unblinding, a treatment comparison is done within each formed risk stratum and stratum-level results are combined for overall statis- tical inference. The impressive power-boosting performance of our proposed 5-step stratified testing and amalgamation routine (5-STAR), relative to that of the logrank test and other common approaches that do not leverage inherently structured patient heterogeneity, is illustrated using a hypothetical and two real datasets along with simulation results. -

Real-Time Process Monitoring and Statistical Process Control for an Automated Casting Facility
Project Number: SYS-SYS7 Real-Time Process Monitoring And Statistical Process Control For an Automated Casting Facility A Major Qualifying Project Report Submitted to the Faculty Of WORCESTER POLYTECHNIC INSTITUTE In partial fulfillment of the requirements for the Degree of Bachelor of Science In Mechanical Engineering By Daniel Lettiere Date: June 2012 Approved: Prof. Satya Shivkumar, Advisor 1 Contents Abstract ......................................................................................................................................4 1. Introduction ............................................................................................................................5 2. Background .............................................................................................................................7 2.1 Manufacturing of Investment Castings .............................................................................7 2.1.1 Origins ........................................................................................................................7 2.1.2 Defects .......................................................................................................................9 2.1.3 Effects of Humidity .....................................................................................................9 2.1.4 Effects of Temperature .............................................................................................10 2.1.5 Effects of Time ..........................................................................................................10 -

Statistics with Free and Open-Source Software
Free and Open-Source Software • the four essential freedoms according to the FSF: • to run the program as you wish, for any purpose • to study how the program works, and change it so it does Statistics with Free and your computing as you wish Open-Source Software • to redistribute copies so you can help your neighbor • to distribute copies of your modified versions to others • access to the source code is a precondition for this Wolfgang Viechtbauer • think of ‘free’ as in ‘free speech’, not as in ‘free beer’ Maastricht University http://www.wvbauer.com • maybe the better term is: ‘libre’ 1 2 General Purpose Statistical Software Popularity of Statistical Software • proprietary (the big ones): SPSS, SAS/JMP, • difficult to define/measure (job ads, articles, Stata, Statistica, Minitab, MATLAB, Excel, … books, blogs/posts, surveys, forum activity, …) • FOSS (a selection): R, Python (NumPy/SciPy, • maybe the most comprehensive comparison: statsmodels, pandas, …), PSPP, SOFA, Octave, http://r4stats.com/articles/popularity/ LibreOffice Calc, Julia, … • for programming languages in general: TIOBE Index, PYPL, GitHut, Language Popularity Index, RedMonk Rankings, IEEE Spectrum, … • note that users of certain software may be are heavily biased in their opinion 3 4 5 6 1 7 8 What is R? History of S and R • R is a system for data manipulation, statistical • … it began May 5, 1976 at: and numerical analysis, and graphical display • simply put: a statistical programming language • freely available under the GNU General Public License (GPL) → open-source -

Applied Biostatistics Applied Biostatistics for the Pulmonologist
APPLIED BIOSTATISTICS FOR THE PULMONOLOGIST DR. VISHWANATH GELLA • Statistics is a way of thinking about the world and decision making-By Sir RA Fisher Why do we need statistics? • A man with one watch always knows what time it is • A man with two watches always searches to identify the correct one • A man with ten watches is always reminded of the difficu lty in measuri ng ti me Objectives • Overview of Biostatistical Terms and Concepts • Application of Statistical Tests Types of statistics • Descriptive Statistics • identify patterns • leads to hypothesis generation • Inferential Statistics • distinguish true differences from random variation • allows hypothesis testing Study design • Analytical studies Case control study(Effect to cause) Cohort study(Cause to effect) • Experimental studies Randomized controlled trials Non-randomized trials Sample size estimation • ‘Too small’ or ‘Too large’ • Sample size depends upon four critical quantities: Type I & II error stat es ( al ph a & b et a errors) , th e vari abilit y of th e d at a (S.D)2 and the effect size(d) • For two group parallel RCT with a continuous outcome - sample size(n) per group = 16(S.D)2/d2 for fixed alpha and beta values • Anti hypertensive trial- effect size= 5 mmHg, S.D of the data- 10 mm Hggp. n= 16 X 100/25= 64 patients per group in the study • Statistical packages - PASS in NCSS, n query or sample power TYPES OF DATA • Quant itat ive (“how muc h?”) or categor ica l variable(“what type?”) • QiiiblQuantitative variables 9 continuous- Blood pressure, height, weight or age 9 Discrete- No.