Circle Drawing Algorithms Third Class
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Models of 2-Dimensional Hyperbolic Space and Relations Among Them; Hyperbolic Length, Lines, and Distances
Models of 2-dimensional hyperbolic space and relations among them; Hyperbolic length, lines, and distances Cheng Ka Long, Hui Kam Tong 1155109623, 1155109049 Course Teacher: Prof. Yi-Jen LEE Department of Mathematics, The Chinese University of Hong Kong MATH4900E Presentation 2, 5th October 2020 Outline Upper half-plane Model (Cheng) A Model for the Hyperbolic Plane The Riemann Sphere C Poincar´eDisc Model D (Hui) Basic properties of Poincar´eDisc Model Relation between D and other models Length and distance in the upper half-plane model (Cheng) Path integrals Distance in hyperbolic geometry Measurements in the Poincar´eDisc Model (Hui) M¨obiustransformations of D Hyperbolic length and distance in D Conclusion Boundary, Length, Orientation-preserving isometries, Geodesics and Angles Reference Upper half-plane model H Introduction to Upper half-plane model - continued Hyperbolic geometry Five Postulates of Hyperbolic geometry: 1. A straight line segment can be drawn joining any two points. 2. Any straight line segment can be extended indefinitely in a straight line. 3. A circle may be described with any given point as its center and any distance as its radius. 4. All right angles are congruent. 5. For any given line R and point P not on R, in the plane containing both line R and point P there are at least two distinct lines through P that do not intersect R. Some interesting facts about hyperbolic geometry 1. Rectangles don't exist in hyperbolic geometry. 2. In hyperbolic geometry, all triangles have angle sum < π 3. In hyperbolic geometry if two triangles are similar, they are congruent. -

More on Parallel and Perpendicular Lines
More on Parallel and Perpendicular Lines By Ma. Louise De Las Peñas et’s look at more problems on parallel and perpendicular lines. The following results, presented Lin the article, “About Slope” will be used to solve the problems. Theorem 1. Let L1 and L2 be two distinct nonvertical lines with slopes m1 and m2, respectively. Then L1 is parallel to L2 if and only if m1 = m2. Theorem 2. Let L1 and L2 be two distinct nonvertical lines with slopes m1 and m2, respectively. Then L1 is perpendicular to L2 if and only if m1m2 = -1. Example 1. The perpendicular bisector of a segment is the line which is perpendicular to the segment at its midpoint. Find equations of the three perpendicular bisectors of the sides of a triangle with vertices at A(-4,1), B(4,5) and C(4,-3). Solution: Consider the triangle with vertices A(-4,1), B(4,5) and C(4,-3), and the midpoints E, F, G of sides AB, BC, and AC, respectively. TATSULOK FirstSecond Year Year Vol. Vol. 12 No.12 No. 1a 2a e-Pages 1 In this problem, our aim is to fi nd the equations of the lines which pass through the midpoints of the sides of the triangle and at the same time are perpendicular to the sides of the triangle. Figure 1 The fi rst step is to fi nd the midpoint of every side. The next step is to fi nd the slope of the lines containing every side. The last step is to obtain the equations of the perpendicular bisectors. -

A Survey on the Square Peg Problem
A survey on the Square Peg Problem Benjamin Matschke∗ March 14, 2014 Abstract This is a short survey article on the 102 years old Square Peg Problem of Toeplitz, which is also called the Inscribed Square Problem. It asks whether every continuous simple closed curve in the plane contains the four vertices of a square. This article first appeared in a more compact form in Notices Amer. Math. Soc. 61(4), 2014. 1 Introduction In 1911 Otto Toeplitz [66] furmulated the following conjecture. Conjecture 1 (Square Peg Problem, Toeplitz 1911). Every continuous simple closed curve in the plane γ : S1 ! R2 contains four points that are the vertices of a square. Figure 1: Example for Conjecture1. A continuous simple closed curve in the plane is also called a Jordan curve, and it is the same as an injective map from the unit circle into the plane, or equivalently, a topological embedding S1 ,! R2. Figure 2: We do not require the square to lie fully inside γ, otherwise there are counter- examples. ∗Supported by Deutsche Telekom Stiftung, NSF Grant DMS-0635607, an EPDI-fellowship, and MPIM Bonn. This article is licensed under a Creative Commons BY-NC-SA 3.0 License. 1 In its full generality Toeplitz' problem is still open. So far it has been solved affirmatively for curves that are \smooth enough", by various authors for varying smoothness conditions, see the next section. All of these proofs are based on the fact that smooth curves inscribe generically an odd number of squares, which can be measured in several topological ways. -

Essential Concepts of Projective Geomtry
Essential Concepts of Projective Geomtry Course Notes, MA 561 Purdue University August, 1973 Corrected and supplemented, August, 1978 Reprinted and revised, 2007 Department of Mathematics University of California, Riverside 2007 Table of Contents Preface : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : i Prerequisites: : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : :iv Suggestions for using these notes : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : :v I. Synthetic and analytic geometry: : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : :1 1. Axioms for Euclidean geometry : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : 1 2. Cartesian coordinate interpretations : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : 2 2 3 3. Lines and planes in R and R : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : 3 II. Affine geometry : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : 7 1. Synthetic affine geometry : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : 7 2. Affine subspaces of vector spaces : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : 13 3. Affine bases: : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : :19 4. Properties of coordinate -

Cyclic Quadrilaterals — the Big Picture Yufei Zhao [email protected]
Winter Camp 2009 Cyclic Quadrilaterals Yufei Zhao Cyclic Quadrilaterals | The Big Picture Yufei Zhao [email protected] An important skill of an olympiad geometer is being able to recognize known configurations. Indeed, many geometry problems are built on a few common themes. In this lecture, we will explore one such configuration. 1 What Do These Problems Have in Common? 1. (IMO 1985) A circle with center O passes through the vertices A and C of triangle ABC and intersects segments AB and BC again at distinct points K and N, respectively. The circumcircles of triangles ABC and KBN intersects at exactly two distinct points B and M. ◦ Prove that \OMB = 90 . B M N K O A C 2. (Russia 1995; Romanian TST 1996; Iran 1997) Consider a circle with diameter AB and center O, and let C and D be two points on this circle. The line CD meets the line AB at a point M satisfying MB < MA and MD < MC. Let K be the point of intersection (different from ◦ O) of the circumcircles of triangles AOC and DOB. Show that \MKO = 90 . C D K M A O B 3. (USA TST 2007) Triangle ABC is inscribed in circle !. The tangent lines to ! at B and C meet at T . Point S lies on ray BC such that AS ? AT . Points B1 and C1 lies on ray ST (with C1 in between B1 and S) such that B1T = BT = C1T . Prove that triangles ABC and AB1C1 are similar to each other. 1 Winter Camp 2009 Cyclic Quadrilaterals Yufei Zhao A B S C C1 B1 T Although these geometric configurations may seem very different at first sight, they are actually very related. -
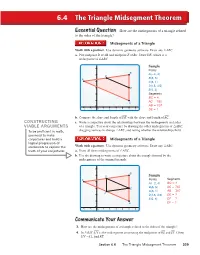
The Triangle Midsegment Theorem
6.4 The Triangle Midsegment Theorem EEssentialssential QQuestionuestion How are the midsegments of a triangle related to the sides of the triangle? Midsegments of a Triangle △ Work with a partner.— Use dynamic geometry— software.— Draw any ABC. a. Plot midpoint D of AB and midpoint E of BC . Draw DE , which is a midsegment of △ABC. Sample 6 Points B A − 5 D ( 2, 4) A B(5, 5) 4 C(5, 1) D(1.5, 4.5) 3 E E(5, 3) 2 Segments BC = 4 1 C AC = 7.62 0 AB = 7.07 −2 −1 0 123456 DE = ? — — b. Compare the slope and length of DE with the slope and length of AC . CONSTRUCTING c. Write a conjecture about the relationships between the midsegments and sides VIABLE ARGUMENTS of a triangle. Test your conjecture by drawing the other midsegments of △ABC, △ To be profi cient in math, dragging vertices to change ABC, and noting whether the relationships hold. you need to make conjectures and build a Midsegments of a Triangle logical progression of △ statements to explore the Work with a partner. Use dynamic geometry software. Draw any ABC. truth of your conjectures. a. Draw all three midsegments of △ABC. b. Use the drawing to write a conjecture about the triangle formed by the midsegments of the original triangle. 6 B 5 D Sample A Points Segments 4 A(−2, 4) BC = 4 B AC = 3 E (5, 5) 7.62 C(5, 1) AB = 7.07 F 2 D(1.5, 4.5) DE = ? E(5, 3) DF = ? 1 C EF = ? 0 −2 −1 0 123456 CCommunicateommunicate YourYour AnswerAnswer 3. -

Plant Leaf Image Detection Method Using a Midpoint Circle Algorithm for Shape-Based Feature Extraction B
Journal of Modern Applied Statistical Methods Volume 16 | Issue 1 Article 26 5-1-2017 Plant Leaf Image Detection Method Using a Midpoint Circle Algorithm for Shape-Based Feature Extraction B. Vijaya Lakshmi K.L.N. College of Engineering, Tamil Nadu, India, [email protected] V. Mohan Thiagarajar College of Engineering, Madurai, Tamil Nadu, India, [email protected] Follow this and additional works at: http://digitalcommons.wayne.edu/jmasm Part of the Applied Statistics Commons, Social and Behavioral Sciences Commons, and the Statistical Theory Commons Recommended Citation Lakshmi, B. V. & Mohan, V. (2017). Plant leaf image detection method using a midpoint circle algorithm for shape-based feature extraction. Journal of Modern Applied Statistical Methods, 16(1), 461-480. doi: 10.22237/jmasm/1493598420 This Regular Article is brought to you for free and open access by the Open Access Journals at DigitalCommons@WayneState. It has been accepted for inclusion in Journal of Modern Applied Statistical Methods by an authorized editor of DigitalCommons@WayneState. Journal of Modern Applied Statistical Methods Copyright © 2017 JMASM, Inc. May 2017, Vol. 16, No. 1, 461-480. ISSN 1538 − 9472 doi: 10.22237/jmasm/1493598420 Plant Leaf Image Detection Method Using a Midpoint Circle Algorithm for Shape-Based Feature Extraction B. Vijaya Lakshmi V. Mohan K.L.N. College of Engineering Thiagarajar College of Engineering Tamil Nadu, India Tamil Nadu, India Shape-based feature extraction in content-based image retrieval is an important research area at present. An algorithm is presented, based on shape features, to enhance the set of features useful in a leaf identification system. -
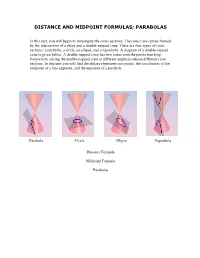
Distance and Midpoint Formulas; Parabolas
DISTANCE AND MIDPOINT FORMULAS; PARABOLAS In this unit, you will begin to investigate the conic sections. The conics are curves formed by the intersection of a plane and a double-napped cone. There are four types of conic sections: a parabola, a circle, an ellipse, and a hyperbola. A diagram of a double-napped cone is given below. A double napped-cone has two cones with the points touching. Notice how slicing the double-napped cone at different angles produces different conic sections. In this unit you will find the distance between two points, the coordinates of the midpoint of a line segment, and the equation of a parabola. Parabola Circle Ellipse Hyperbola Distance Formula Midpoint Formula Parabolas Distance Formula The distance between two points, A( x1,y 1 ) and B( x22, y ), on a coordinate plane is as follows: 22 dxxyy()()21 21 *the order of x and y does not matter. Example #1: Find the distance between point S which is located at (3, 5) and point T which is located at (–4, –2). d (4 3)22 (2 5) d (7)22 (7) d 49 49 d 98 d 49 2 d 72 The distance between S(3, 5) and T(–4, –2) is 72. Midpoint Formula The coordinates of the midpoint, M, between two points A(,x y ) and B (,x y ) can be 11 22 found using the following formula: x1212 xy y M , 22 Example #1: Find the coordinates of the midpoint between point P which is located at (–3, 2) and point Q which is located at (5, –2). -

Determine Whether Each Quadrilateral Is a Parallelogram. Justify Your
6-3 Tests for Parallelograms Determine whether each quadrilateral is a 3. KITES Charmaine is building the kite shown below. parallelogram. Justify your answer. She wants to be sure that the string around her frame forms a parallelogram before she secures the material to it. How can she use the measures of the wooden portion of the frame to prove that the string forms a parallelogram? Explain your reasoning. 1. SOLUTION: From the figure, all 4 angles are congruent. Since each pair of opposite angles are congruent, the quadrilateral is a parallelogram by Theorem 6.10. ANSWER: Yes; each pair of opposite angles are congruent. SOLUTION: Charmaine can use Theorem 6.11 to determine if the string forms a parallelogram. If the diagonals of a 2. quadrilateral bisect each other, then the quadrilateral is a parallelogram, so if AP = CP and BP = DP, then SOLUTION: the string forms a parallelogram. We cannot get any information on the angles, so we cannot meet the conditions of Theorem 6.10. We ANSWER: cannot get any information on the sides, so we cannot AP = CP, BP = DP; Sample answer: If the diagonals meet the conditions of Theorems 6.9 or 6.12. One of of a quadrilateral bisect each other, then the the diagonals is bisected, but the other diagonal is not quadrilateral is a parallelogram, so if AP = CP and because it is split into unequal sides. So, the BP = DP, then the string forms a parallelogram. conditions of Theorem 6.11 are not met. Therefore, the figure is not a parallelogram. -

Exploring Cyclic Quadrilaterals with Perpendicular Diagonals
North American GeoGebra Journal Volume 4, Number 1, ISSN 2162-3856 EXPLORING CYCLIC QUADRILATERALS WITH PERPENDICULAR DIAGONALS Alfinio Flores University of Delaware Abstract After a brief discussion of two preliminary activities, the author presents three student explo- rations about cyclic quadrilaterals with perpendicular diagonals and an extension to cyclical quadrilaterals. In the first exploration, students explore the relationships among the intersection of the segments joining midpoints of opposite sides, the intersection of the diagonals, and the center of the circle. In the second, the relationship between the sums of squares of opposite sides and the square of the radius is examined. In the third, students explore properties of a line per- pendicular to a side through the intersection of the diagonals. Lastly, students are introduced to the concept of anticenter as they extend one of the results to cyclic quadrilaterals in general. Keywords: Cyclic Quadrilaterals 1 INTRODUCTION 1.1 Overview Students explore quadrilaterals that satisfy two conditions - namely, 1) they are cyclical, that is, their four vertices lie on a circle, and 2) their diagonals are perpendicular to each other. With GeoGebra [2] it is straightforward to construct such quadrilaterals using the coordinate axes and the circle tool, as suggested in Figure 1). In two preliminary activities, students explore Varignon’s theorem for quadrilaterals and a result about the intersection of lines that connect midpoints of opposite sides of a quadrilateral. After three follow-up explorations, students extend one of the results to a general cyclical quadrilateral. 1.2 Background knowledge Students only need basic knowledge of GeoGebra to explore and discover the results discussed in this paper. -

The Rectangular Peg Problem
The rectangular peg problem joint work with Andrew Lobb (Durham / OIST) Josh Greene (Boston College) BIRS June 11, 2020 Josh Greene The rectangular peg problem Motivation. In 1911, Otto Toeplitz posed the following question: Problem 1 (The Square Peg Problem) Does every continuous Jordan curve in the Euclidean plane contain four points at the vertices of a square? It posits a striking connection between the topology and the geometry of the Euclidean plane. It remains open to this day. Josh Greene The rectangular peg problem Jordan curves. Josh Greene The rectangular peg problem Inscribed squares. Josh Greene The rectangular peg problem Why squares / quadrilaterals? I Three points are ubiquitous: 8 triangle T and 8 Jordan curve γ, γ inscribes a triangle similar to T . (Exercise.) I Five points are not: dissimilar ellipses inscribe dissimilar pentagons. (Distinct ellipses meet in at most four points.) I Four is where things get interesting: a recurring theme in low-dimensional topology / geometry. Josh Greene The rectangular peg problem Early progress. I Emch (1913) solved the problem for smooth convex curves. (Ideas involving configuration spaces, homology) I Schnirelman (1929) solved it for smooth Jordan curves. In fact, a generic smooth Jordan curve contains an odd number of \inscribed" squares. (Bordism argument) Tempting approach to original problem: a limiting argument. Any continuous Jordan curve is a limit of smooth ones, so take a limiting sequence of squares. Problem: the squares may shrink to points. Josh Greene The rectangular peg problem Variations. I Varying regularity condition on curve (e.g. recent work of Feller-Golla, Schwartz, Tao). -

Segment Length and Midpoint
Segment Length and Midpoint The most basic figures in geometry are undefined terms, which cannot be defined using other figures. When you name a plane, does the order of the letters matter? The word between is another undefined term, but its meaning is understood from its use in everyday language. Example 1: Draw two points J and K. Then draw a line through them. Example 2: Draw two points J and K. Then draw a line segment with endpoints J and K. Example 3: Draw point K and draw a ray from endpoint K. Plot a point J along the ray. Example 4: Draw three points J, K, and M so that they are not all on the same line. Then draw the plane that contains the three points. Example 5: Give a name for each of the figures you drew. Then tell if the figure is an undefined term or a defined term. Point _________________ Line __________________ Segment _______________ Ray __________________ Plane __________________ Would be the same as ? If and are different names for the same line, what must be true about points P, Q, R, and S? Points that lie in the same plane are coplanar. Lines that lie in the same plane but do not intersect are parallel. Points that lie on the same line are collinear. A postulate is a statement that is accepted as true without proof. A construction is a geometric drawing that produces an accurate representation without using numbers or measures. Example 6: Use a compass and straightedge to construct a segments whose length is AB + CD Distance Formula: From the picture, what other methods can you come up with to determine the distance between two points? Example 7: Determine whether the given segments have the same length.