Inscribed Rectangles in a Kite and a Solution to 2017-1 Problem 5
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Models of 2-Dimensional Hyperbolic Space and Relations Among Them; Hyperbolic Length, Lines, and Distances
Models of 2-dimensional hyperbolic space and relations among them; Hyperbolic length, lines, and distances Cheng Ka Long, Hui Kam Tong 1155109623, 1155109049 Course Teacher: Prof. Yi-Jen LEE Department of Mathematics, The Chinese University of Hong Kong MATH4900E Presentation 2, 5th October 2020 Outline Upper half-plane Model (Cheng) A Model for the Hyperbolic Plane The Riemann Sphere C Poincar´eDisc Model D (Hui) Basic properties of Poincar´eDisc Model Relation between D and other models Length and distance in the upper half-plane model (Cheng) Path integrals Distance in hyperbolic geometry Measurements in the Poincar´eDisc Model (Hui) M¨obiustransformations of D Hyperbolic length and distance in D Conclusion Boundary, Length, Orientation-preserving isometries, Geodesics and Angles Reference Upper half-plane model H Introduction to Upper half-plane model - continued Hyperbolic geometry Five Postulates of Hyperbolic geometry: 1. A straight line segment can be drawn joining any two points. 2. Any straight line segment can be extended indefinitely in a straight line. 3. A circle may be described with any given point as its center and any distance as its radius. 4. All right angles are congruent. 5. For any given line R and point P not on R, in the plane containing both line R and point P there are at least two distinct lines through P that do not intersect R. Some interesting facts about hyperbolic geometry 1. Rectangles don't exist in hyperbolic geometry. 2. In hyperbolic geometry, all triangles have angle sum < π 3. In hyperbolic geometry if two triangles are similar, they are congruent. -

Build a Tetrahedral Kite
Aeronautics Research Mission Directorate Build a Tetrahedral Kite Suggested Grades: 8-12 Activity Overview Time: 90-120 minutes In this activity, you will build a tetrahedral kite from Materials household supplies. • 24 straws (8 inches or less) - NOTE: The straws need to be Steps straight and the same length. If only flexible straws are available, 1. Cut a length of yarn/string 4 feet long. then cut off the flexible portion. • Two or three large spools of 2. Take six straws and place them on a flat surface. cotton string or yarn (approximately 100 feet total) 3. Use your piece of string to join three straws • Scissors together in a triangular shape. On the side where • Hot glue gun and hot glue sticks the two strings are extending from it, one end • Ruler or dowel rod for kite bridle should be approximately 20 inches long, and the • Four pieces of tissue paper (24 x other should be approximately 4 inches long. 18 inches or larger) See Figure 1. • All-purpose glue stick Figure 1 4. Tie these two ends of the string tightly together. Make sure there is no room for the triangle to wiggle. 5. The three straws should form a tight triangle. 6. Cut another 4-inch piece of string. 7. Take one end of the 4-inch string, and tie that end to a corner of the triangle that does not have the string ends extending from it. Figure 2. 8. Add two more straws onto the longest piece of string. 9. Next, take the string that holds the two additional straws and tie it to the end of one of the 4-inch strings to make another tight triangle. -

More on Parallel and Perpendicular Lines
More on Parallel and Perpendicular Lines By Ma. Louise De Las Peñas et’s look at more problems on parallel and perpendicular lines. The following results, presented Lin the article, “About Slope” will be used to solve the problems. Theorem 1. Let L1 and L2 be two distinct nonvertical lines with slopes m1 and m2, respectively. Then L1 is parallel to L2 if and only if m1 = m2. Theorem 2. Let L1 and L2 be two distinct nonvertical lines with slopes m1 and m2, respectively. Then L1 is perpendicular to L2 if and only if m1m2 = -1. Example 1. The perpendicular bisector of a segment is the line which is perpendicular to the segment at its midpoint. Find equations of the three perpendicular bisectors of the sides of a triangle with vertices at A(-4,1), B(4,5) and C(4,-3). Solution: Consider the triangle with vertices A(-4,1), B(4,5) and C(4,-3), and the midpoints E, F, G of sides AB, BC, and AC, respectively. TATSULOK FirstSecond Year Year Vol. Vol. 12 No.12 No. 1a 2a e-Pages 1 In this problem, our aim is to fi nd the equations of the lines which pass through the midpoints of the sides of the triangle and at the same time are perpendicular to the sides of the triangle. Figure 1 The fi rst step is to fi nd the midpoint of every side. The next step is to fi nd the slope of the lines containing every side. The last step is to obtain the equations of the perpendicular bisectors. -

A Survey on the Square Peg Problem
A survey on the Square Peg Problem Benjamin Matschke∗ March 14, 2014 Abstract This is a short survey article on the 102 years old Square Peg Problem of Toeplitz, which is also called the Inscribed Square Problem. It asks whether every continuous simple closed curve in the plane contains the four vertices of a square. This article first appeared in a more compact form in Notices Amer. Math. Soc. 61(4), 2014. 1 Introduction In 1911 Otto Toeplitz [66] furmulated the following conjecture. Conjecture 1 (Square Peg Problem, Toeplitz 1911). Every continuous simple closed curve in the plane γ : S1 ! R2 contains four points that are the vertices of a square. Figure 1: Example for Conjecture1. A continuous simple closed curve in the plane is also called a Jordan curve, and it is the same as an injective map from the unit circle into the plane, or equivalently, a topological embedding S1 ,! R2. Figure 2: We do not require the square to lie fully inside γ, otherwise there are counter- examples. ∗Supported by Deutsche Telekom Stiftung, NSF Grant DMS-0635607, an EPDI-fellowship, and MPIM Bonn. This article is licensed under a Creative Commons BY-NC-SA 3.0 License. 1 In its full generality Toeplitz' problem is still open. So far it has been solved affirmatively for curves that are \smooth enough", by various authors for varying smoothness conditions, see the next section. All of these proofs are based on the fact that smooth curves inscribe generically an odd number of squares, which can be measured in several topological ways. -

Performance Based Learning and Assessment Task Kite Project
Performance Based Learning and Assessment Task Kite Project I. ASSESSSMENT TASK OVERVIEW & PURPOSE: The students are instructed to: research the history, science, and design of kites; design a blueprint of their kite and find the measurements, scale factor, area, and perimeter of their blueprint; and construct and fly their kite. II. UNIT AUTHOR: Leslie Hindman, Washington-Lee High School, Arlington Public Schools III. COURSE: Geometry IV. CONTENT STRAND: Geometry, Measurement V. OBJECTIVES: Students will be able to • Design a scale model of a kite • Measure the dimensions and angles of the scale model • Determine the scale factor of the scale model • Compute the area and perimeter of the scale model • Construct and fly a kite VI. REFERENCE/RESOURCE MATERIALS: For Research: computer access For Scale Model Drawing: ruler, protractor, graph paper, calculator, Geometry SOL formula sheet For Kites: tissue paper, plastic table cloths, small wooden dowels, straws, yarn, fishing wire, markers, scissors, tape, glue VII. PRIMARY ASSESSMENT STRATEGIES: The task includes an assessment component that performs two functions: (1) for the student it will be a checklist and provide a self-assessment and (2) for the teacher it will be used as a rubric. The attached assessment list will assess the research section, scale model drawing, and kite construction. VIII. EVALUATION CRITERIA: Assessment List, corresponding rubric. IX. INSTRUCTIONAL TIME: 2 ninety minute class periods for research, scale model drawings, and kite construction. 1/2 ninety minute class period for flying kites. Kite Project Strand Geometry, Measurement Mathematical Objective(s) Students will be able to: • Design a scale model of a kite • Find the measures of the sides and angles of the scale model • Determine the scale factor of the scale model • Compute the area and perimeter of the scale model Related SOL • G.12 The student will make a model of a three-dimensional figure from a two- dimensional drawing and make a two-dimensional representation of a three- dimensional object. -

Essential Concepts of Projective Geomtry
Essential Concepts of Projective Geomtry Course Notes, MA 561 Purdue University August, 1973 Corrected and supplemented, August, 1978 Reprinted and revised, 2007 Department of Mathematics University of California, Riverside 2007 Table of Contents Preface : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : i Prerequisites: : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : :iv Suggestions for using these notes : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : :v I. Synthetic and analytic geometry: : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : :1 1. Axioms for Euclidean geometry : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : 1 2. Cartesian coordinate interpretations : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : 2 2 3 3. Lines and planes in R and R : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : 3 II. Affine geometry : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : 7 1. Synthetic affine geometry : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : 7 2. Affine subspaces of vector spaces : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : 13 3. Affine bases: : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : :19 4. Properties of coordinate -

INTRODUCTION to QUADRILATERALS Square Rectangle Rhombus Parallelogram
INTRODUCTION TO QUADRILATERALS square rectangle rhombus parallelogram trapezoid kite Mathematicians define regular quadrilaterals according to their attributes. a) Quadrilaterals are two-dimensional closed figures that have four sides and four angles. b) The sum of their four angles is 360 degrees. c) When we trace diagonals from one opposite corner to another in a quadrilateral, these lines always intersect (pass it through) and in some cases they bisect (cut the other line in half). d) Regular quadrilaterals are named square, rectangle, parallelogram, rhombus, trapezoid, and kite. e) VERY IMPORTANT TO REMEMBER THIS! : Although these are the names of the quadrilaterals, these words are also the names of groups of quadrilaterals. Each group has its own characteristics or attributes that distinguish them from the others. For instance, the figure square belongs obviously to the group of squares, but also belongs to the groups of trapezoids, parallelograms, rectangles, rhombuses, and kites, because it shares similar attributes with them. However, the group of squares has only one figure: square. This is because no other quadrilateral shares the attributes of the squares, which are having four equal sides and four right angles. TRAPEZOIDS a) Trapezoids form the largest group of quadrilaterals. They include the figures of square, rectangle, parallelogram, rhombus, and of course, trapezoid. (the figure kite does not belong to the group of trapezoids) b) Trapezoids have only one attribute: they have at least one parallel line. Also, a. They may or may not have two or even four equal in length sides. b. They may or may not have opposite sides of the same length c. -

Cyclic Quadrilaterals — the Big Picture Yufei Zhao [email protected]
Winter Camp 2009 Cyclic Quadrilaterals Yufei Zhao Cyclic Quadrilaterals | The Big Picture Yufei Zhao [email protected] An important skill of an olympiad geometer is being able to recognize known configurations. Indeed, many geometry problems are built on a few common themes. In this lecture, we will explore one such configuration. 1 What Do These Problems Have in Common? 1. (IMO 1985) A circle with center O passes through the vertices A and C of triangle ABC and intersects segments AB and BC again at distinct points K and N, respectively. The circumcircles of triangles ABC and KBN intersects at exactly two distinct points B and M. ◦ Prove that \OMB = 90 . B M N K O A C 2. (Russia 1995; Romanian TST 1996; Iran 1997) Consider a circle with diameter AB and center O, and let C and D be two points on this circle. The line CD meets the line AB at a point M satisfying MB < MA and MD < MC. Let K be the point of intersection (different from ◦ O) of the circumcircles of triangles AOC and DOB. Show that \MKO = 90 . C D K M A O B 3. (USA TST 2007) Triangle ABC is inscribed in circle !. The tangent lines to ! at B and C meet at T . Point S lies on ray BC such that AS ? AT . Points B1 and C1 lies on ray ST (with C1 in between B1 and S) such that B1T = BT = C1T . Prove that triangles ABC and AB1C1 are similar to each other. 1 Winter Camp 2009 Cyclic Quadrilaterals Yufei Zhao A B S C C1 B1 T Although these geometric configurations may seem very different at first sight, they are actually very related. -

When Is a Tangential Quadrilateral a Kite?
Forum Geometricorum b Volume 11 (2011) 165–174. b b FORUM GEOM ISSN 1534-1178 When is a Tangential Quadrilateral a Kite? Martin Josefsson Abstract. We prove 13 necessary and sufficient conditions for a tangential quadri- lateral to be a kite. 1. Introduction A tangential quadrilateral is a quadrilateral that has an incircle. A convex quadrilateral with the sides a, b, c, d is tangential if and only if a + c = b + d (1) according to the Pitot theorem [1, pp.65–67]. A kite is a quadrilateral that has two pairs of congruent adjacent sides. Thus all kites has an incircle since its sides satisfy (1). The question we will answer here concerns the converse, that is, what additional property a tangential quadrilateral must have to be a kite? We shall prove 13 such conditions. To prove two of them we will use a formula for the area of a tangential quadrilateral that is not so well known, so we prove it here first. It is given as a problem in [4, p.29]. Theorem 1. A tangential quadrilateral with sides a, b, c, d and diagonals p,q has the area 1 2 2 K = 2 (pq) − (ac − bd) . p Proof. A convex quadrilateral with sides a, b, c, d and diagonals p,q has the area 1 2 2 2 2 2 2 2 K = 4 4p q − (a − b + c − d ) (2) p according to [6] and [14]. Squaring the Pitot theorem (1) yields 2 2 2 2 a + c + 2ac = b + d + 2bd. (3) Using this in (2), we get 1 2 2 K = 4 4(pq) − (2bd − 2ac) p and the formula follows. -

Cyclic and Bicentric Quadrilaterals G
Cyclic and Bicentric Quadrilaterals G. T. Springer Email: [email protected] Hewlett-Packard Calculators and Educational Software Abstract. In this hands-on workshop, participants will use the HP Prime graphing calculator and its dynamic geometry app to explore some of the many properties of cyclic and bicentric quadrilaterals. The workshop will start with a brief introduction to the HP Prime and an overview of its features to get novice participants oriented. Participants will then use ready-to-hand constructions of cyclic and bicentric quadrilaterals to explore. Part 1: Cyclic Quadrilaterals The instructor will send you an HP Prime app called CyclicQuad for this part of the activity. A cyclic quadrilateral is a convex quadrilateral that has a circumscribed circle. 1. Press ! to open the App Library and select the CyclicQuad app. The construction consists DEGH, a cyclic quadrilateral circumscribed by circle A. 2. Tap and drag any of the points D, E, G, or H to change the quadrilateral. Which of the following can DEGH never be? • Square • Rhombus (non-square) • Rectangle (non-square) • Parallelogram (non-rhombus) • Isosceles trapezoid • Kite Just move the points of the quadrilateral around enough to convince yourself for each one. Notice HDE and HE are both inscribed angles that subtend the entirety of the circle; ≮ ≮ likewise with DHG and DEG. This leads us to a defining characteristic of cyclic ≮ ≮ quadrilaterals. Make a conjecture. A quadrilateral is cyclic if and only if… 3. Make DEGH into a kite, similar to that shown to the right. Tap segment HE and press E to select it. Now use U and D to move the diagonal vertically. -
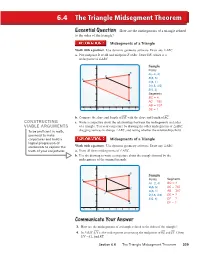
The Triangle Midsegment Theorem
6.4 The Triangle Midsegment Theorem EEssentialssential QQuestionuestion How are the midsegments of a triangle related to the sides of the triangle? Midsegments of a Triangle △ Work with a partner.— Use dynamic geometry— software.— Draw any ABC. a. Plot midpoint D of AB and midpoint E of BC . Draw DE , which is a midsegment of △ABC. Sample 6 Points B A − 5 D ( 2, 4) A B(5, 5) 4 C(5, 1) D(1.5, 4.5) 3 E E(5, 3) 2 Segments BC = 4 1 C AC = 7.62 0 AB = 7.07 −2 −1 0 123456 DE = ? — — b. Compare the slope and length of DE with the slope and length of AC . CONSTRUCTING c. Write a conjecture about the relationships between the midsegments and sides VIABLE ARGUMENTS of a triangle. Test your conjecture by drawing the other midsegments of △ABC, △ To be profi cient in math, dragging vertices to change ABC, and noting whether the relationships hold. you need to make conjectures and build a Midsegments of a Triangle logical progression of △ statements to explore the Work with a partner. Use dynamic geometry software. Draw any ABC. truth of your conjectures. a. Draw all three midsegments of △ABC. b. Use the drawing to write a conjecture about the triangle formed by the midsegments of the original triangle. 6 B 5 D Sample A Points Segments 4 A(−2, 4) BC = 4 B AC = 3 E (5, 5) 7.62 C(5, 1) AB = 7.07 F 2 D(1.5, 4.5) DE = ? E(5, 3) DF = ? 1 C EF = ? 0 −2 −1 0 123456 CCommunicateommunicate YourYour AnswerAnswer 3. -

Angle Bisectors in a Quadrilateral Are Concurrent
Angle Bisectors in a Quadrilateral in the classroom A Ramachandran he bisectors of the interior angles of a quadrilateral are either all concurrent or meet pairwise at 4, 5 or 6 points, in any case forming a cyclic quadrilateral. The situation of exactly three bisectors being concurrent is not possible. See Figure 1 for a possible situation. The reader is invited to prove these as well as observations regarding some of the special cases mentioned below. Start with the last observation. Assume that three angle bisectors in a quadrilateral are concurrent. Join the point of T D E H A F G B C Figure 1. A typical configuration, showing how a cyclic quadrilateral is formed Keywords: Quadrilateral, diagonal, angular bisector, tangential quadrilateral, kite, rhombus, square, isosceles trapezium, non-isosceles trapezium, cyclic, incircle 33 At Right Angles | Vol. 4, No. 1, March 2015 Vol. 4, No. 1, March 2015 | At Right Angles 33 D A D A D D E G A A F H G I H F F G E H B C E Figure 3. If is a parallelogram, then is a B C B C rectangle B C Figure 2. A tangential quadrilateral Figure 6. The case when is a non-isosceles trapezium: the result is that is a cyclic Figure 7. The case when has but A D quadrilateral in which : the result is that is an isosceles ∘ trapezium ( and ∠ ) E ∠ ∠ ∠ ∠ concurrence to the fourth vertex. Prove that this line indeed bisects the angle at the fourth vertex. F H Tangential quadrilateral A quadrilateral in which all the four angle bisectors G meet at a pointincircle is a — one which has an circle touching all the four sides.