Verification with Proof Score of Arithmetic Expression Compiler
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-
Process and Memory Management Commands
Process and Memory Management Commands This chapter describes the Cisco IOS XR software commands used to manage processes and memory. For more information about using the process and memory management commands to perform troubleshooting tasks, see Cisco ASR 9000 Series Aggregation Services Router Getting Started Guide. • clear context, on page 2 • dumpcore, on page 3 • exception coresize, on page 6 • exception filepath, on page 8 • exception pakmem, on page 12 • exception sparse, on page 14 • exception sprsize, on page 16 • follow, on page 18 • monitor threads, on page 25 • process, on page 29 • process core, on page 32 • process mandatory, on page 34 • show context, on page 36 • show dll, on page 39 • show exception, on page 42 • show memory, on page 44 • show memory compare, on page 47 • show memory heap, on page 50 • show processes, on page 54 Process and Memory Management Commands 1 Process and Memory Management Commands clear context clear context To clear core dump context information, use the clear context command in the appropriate mode. clear context location {node-id | all} Syntax Description location{node-id | all} (Optional) Clears core dump context information for a specified node. The node-id argument is expressed in the rack/slot/module notation. Use the all keyword to indicate all nodes. Command Default No default behavior or values Command Modes Administration EXEC EXEC mode Command History Release Modification Release 3.7.2 This command was introduced. Release 3.9.0 No modification. Usage Guidelines To use this command, you must be in a user group associated with a task group that includes appropriate task IDs. -

Process Management
Princeton University Computer Science 217: Introduction to Programming Systems Process Management 1 Goals of this Lecture Help you learn about: • Creating new processes • Waiting for processes to terminate • Executing new programs • Shell structure Why? • Creating new processes and executing new programs are fundamental tasks of many utilities and end-user applications • Assignment 7… 2 System-Level Functions As noted in the Exceptions and Processes lecture… Linux system-level functions for process management Function Description exit() Terminate the process fork() Create a child process wait() Wait for child process termination execvp() Execute a program in current process getpid() Return the process id of the current process 3 Agenda Creating new processes Waiting for processes to terminate Executing new programs Shell structure 4 Why Create New Processes? Why create a new process? • Scenario 1: Program wants to run an additional instance of itself • E.g., web server receives request; creates additional instance of itself to handle the request; original instance continues listening for requests • Scenario 2: Program wants to run a different program • E.g., shell receives a command; creates an additional instance of itself; additional instance overwrites itself with requested program to handle command; original instance continues listening for commands How to create a new process? • A “parent” process forks a “child” process • (Optionally) child process overwrites itself with a new program, after performing appropriate setup 5 fork System-Level -
How to Write a File Copy Program in Standard C? #Include <Stdio.H>
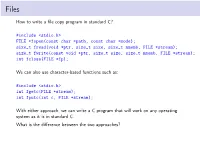
Files How to write a file copy program in standard C? #include <stdio.h> FILE *fopen(const char *path, const char *mode); size_t fread(void *ptr, size_t size, size_t nmemb, FILE *stream); size_t fwrite(const void *ptr, size_t size, size_t nmemb, FILE *stream); int fclose(FILE *fp); We can also use character-based functions such as: #include <stdio.h> int fgetc(FILE *stream); int fputc(int c, FILE *stream); With either approach, we can write a C program that will work on any operating system as it is in standard C. What is the difference between the two approaches? /* lab/stdc-mycp.c */ /* appropriate header files */ #define BUF_SIZE 65536 int main(int argc, char *argv[]) { FILE *src, *dst; size_t in, out; char buf[BUF_SIZE]; int bufsize; if (argc != 4) { fprintf(stderr, "Usage: %s <buffer size> <src> <dest>\n", argv[0]); exit(1); } bufsize = atoi(argv[1]); if (bufsize > BUF_SIZE) { fprintf(stderr,"Error: %s: max. buffer size is %d\n",argv[0], BUF_SIZE); exit(1); } src = fopen(argv[2], "r"); if (NULL == src) exit(2); dst = fopen(argv[3], "w"); if (dst < 0) exit(3); while (1) { in = fread(buf, 1, bufsize, src); if (0 == in) break; out = fwrite(buf, 1, in, dst); if (0 == out) break; } fclose(src); fclose(dst); exit(0); } POSIX/Unix File Interface The system call interface for files in POSIX systems like Linux and MacOSX. A file is a named, ordered stream of bytes. I open(..) Open a file for reading or writing. Also allows a file to be locked providing exclusive access. I close(..) I read(..) The read operation is normally blocking. -

Operating System Lab Manual
OPERATING SYSTEM LAB MANUAL BASICS OF UNIX COMMANDS Ex.No:1.a INTRODUCTION TO UNIX AIM: To study about the basics of UNIX UNIX: It is a multi-user operating system. Developed at AT & T Bell Industries, USA in 1969. Ken Thomson along with Dennis Ritchie developed it from MULTICS (Multiplexed Information and Computing Service) OS. By1980, UNIX had been completely rewritten using C langua ge. LINUX: It is similar to UNIX, which is created by Linus Torualds. All UNIX commands works in Linux. Linux is a open source software. The main feature of Linux is coexisting with other OS such as windows and UNIX. STRUCTURE OF A LINUXSYSTEM: It consists of three parts. a)UNIX kernel b) Shells c) Tools and Applications UNIX KERNEL: Kernel is the core of the UNIX OS. It controls all tasks, schedule all Processes and carries out all the functions of OS. Decides when one programs tops and another starts. SHELL: Shell is the command interpreter in the UNIX OS. It accepts command from the user and analyses and interprets them 1 | P a g e BASICS OF UNIX COMMANDS Ex.No:1.b BASIC UNIX COMMANDS AIM: To study of Basic UNIX Commands and various UNIX editors such as vi, ed, ex and EMACS. CONTENT: Note: Syn->Syntax a) date –used to check the date and time Syn:$date Format Purpose Example Result +%m To display only month $date+%m 06 +%h To display month name $date+%h June +%d To display day of month $date+%d O1 +%y To display last two digits of years $date+%y 09 +%H To display hours $date+%H 10 +%M To display minutes $date+%M 45 +%S To display seconds $date+%S 55 b) cal –used to display the calendar Syn:$cal 2 2009 c)echo –used to print the message on the screen. -

System Calls & Signals
CS345 OPERATING SYSTEMS System calls & Signals Panagiotis Papadopoulos [email protected] 1 SYSTEM CALL When a program invokes a system call, it is interrupted and the system switches to Kernel space. The Kernel then saves the process execution context (so that it can resume the program later) and determines what is being requested. The Kernel carefully checks that the request is valid and that the process invoking the system call has enough privilege. For instance some system calls can only be called by a user with superuser privilege (often referred to as root). If everything is good, the Kernel processes the request in Kernel Mode and can access the device drivers in charge of controlling the hardware (e.g. reading a character inputted from the keyboard). The Kernel can read and modify the data of the calling process as it has access to memory in User Space (e.g. it can copy the keyboard character into a buffer that the calling process has access to) When the Kernel is done processing the request, it restores the process execution context that was saved when the system call was invoked, and control returns to the calling program which continues executing. 2 SYSTEM CALLS FORK() 3 THE FORK() SYSTEM CALL (1/2) • A process calling fork()spawns a child process. • The child is almost an identical clone of the parent: • Program Text (segment .text) • Stack (ss) • PCB (eg. registers) • Data (segment .data) #include <sys/types.h> #include <unistd.h> pid_t fork(void); 4 THE FORK() SYSTEM CALL (2/2) • The fork()is one of the those system calls, which is called once, but returns twice! Consider a piece of program • After fork()both the parent and the child are .. -

Computer Systems II Behind the 'System(…)' Command Execv Execl
Computer Systems II Execung Processes 1 Behind the ‘system(…)’ Command execv execl 2 1 Recall: system() Example call: system(“mkdir systest”); • mkdir is the name of the executable program • systest is the argument passed to the executable mkdir.c int main(int argc, char * argv[]) { ... // create directory called argv[1] ... } Unix’s execv The system call execv executes a file, transforming the calling process into a new process. ADer a successful execv, there is no return to the calling process. execv(const char * path, const char * argv[]) • path is the full path for the file to be executed • argv is the argument array, starEng with the program name • each argument is a null-terminated string • the first argument is the name of the program • the last entry in argv is NULL 2 system() vs. execv system(“mkdir systest”); mkdir.c int main(int argc, char * argv[]) { ... // create directory called argv[1] ... } char * argv[] = {“/bin/mkdir”, “systest”, NULL}; execv(argv[0], argv); How execv Works (1) pid = 25 pid = 26 Data Resources Data Text Text Stack Stack PCB File PCB char * argv[ ] = {“/bin/ls”, 0}; cpid = 26 cpid = 0 char * argv[ ] = {“/bin/ls”, 0}; <…> <…> int cpid = fork( ); int cpid = fork( ); if (cpid = = 0) { if (cpid = = 0) { execv(argv[0], argv); execv(argv[0], argv); exit(0); exit(0); } } <parent code> <parent code> wait(&cpid); wait(&cpid); /bin/ls UNIX kernel 3 How execv Works (2) pid = 25 pid = 26 Data Resources Text Stack PCB File char * argv[ ] = {“/bin/ls”, 0}; cpid = 26 <…> Exec destroys the int cpid = fork( ); if (cpid = = 0) { process image of the execv(argv[0], argv); calling process. -

Optimizing Latency and Throughput for Spawning Processes on Massively Multicore Processors
Optimizing Latency and Throughput for Spawning Processes on Massively Multicore Processors Abhishek Kulkarni*, Michael Lang¶, Latchesar Ionkov¶ and Andrew Lumsdaine* *Center for Research in Extreme Scale Technologies (CREST) Indiana University, Bloomington ¶ Ultrascale Systems Research Center New Mexico Consortium Los Alamos National Laboratory June 29 2012 1 The Exascale Era • “Going to the exascale” is a challenging venture • Clock rates and ILP have reached points of diminishing returns • Memory and Power wall limits performance • Higher soA and hard error rates at smaller feature sizes • Massive intra-node parallelism • Manycore processors and integrated accelerators • Intel MIC (Knights Ferry, Knights Corner) • Tilera Tile Gx 2 We need transformation, not evolution • Emerging hardware will drive the transformaon of the tradiKonal soAware stack • New programming models, execuKon models, runKme systems and operang systems Applications Applications Compilers Libraries Compilers Libraries Runtime System Operating System Execution Model Virtual Machine Host OS Lightweight Kernel HW Abstraction Layer HW Abstraction Layer Hardware Hardware 3 Challenges • New operang systems and lightweight kernels • Tessellaon, Barrelfish, KiOen, fos • Nave operang system (OS) support for accelerators • EvoluKonary approaches • IdenKfying potenKal bo+lenecks in exisKng operang systems (Linux) • OS scalability efforts such as parKKoning, many-core inter-processor communicaon, symbioKc execuKon, virtualizaon. 4 Optimizing process management • Reducing the latency to spawn new processes locally results in faster global job launch • Emerging dynamic and resilient execuKon models are considering the feasibility of maintaining process pools for fault isolaon • Higher throughput makes such runKme systems viable • Memory overcomming can lead to unpredictable behavior including excessive swapping or OOM killing random processes • OpKmizing memory locality and NUMA-aware process spawning 5 “Process control in its modern form was designed and implemented within a couple of days. -

Unix Login Profile
Unix login Profile A general discussion of shell processes, shell scripts, shell functions and aliases is a natural lead in for examining the characteristics of the login profile. The term “shell” is used to describe the command interpreter that a user runs to interact with the Unix operating system. When you login, a shell process is initiated for you, called your login shell. There are a number of "standard" command interpreters available on most Unix systems. On the UNF system, the default command interpreter is the Korn shell which is determined by the user’s entry in the /etc/passwd file. From within the login environment, the user can run Unix commands, which are just predefined processes, most of which are within the system directory named /usr/bin. A shell script is just a file of commands, normally executed at startup for a shell process that was spawned to run the script. The contents of this file can just be ordinary commands as would be entered at the command prompt, but all standard command interpreters also support a scripting language to provide control flow and other capabilities analogous to those of high level languages. A shell function is like a shell script in its use of commands and the scripting language, but it is maintained in the active shell, rather than in a file. The typically used definition syntax is: <function-name> () { <commands> } It is important to remember that a shell function only applies within the shell in which it is defined (not its children). Functions are usually defined within a shell script, but may also be entered directly at the command prompt. -

Operating Systems Homework Assignment 2
Operating Systems Homework Assignment 2 Preparation For this homework assignment, you need to get familiar with a Linux system (Ubuntu, Fedora, CentOS, etc.). There are two options to run Linux on your Desktop (or Laptop) computer: 1. Run a copy of a virtual machine freely available on-line in your own PC environment using Virtual Box. Create your own Linux virtual machine (Linux as a guest operating system) in Windows. You may consider installing MS Windows as a guest OS in Linux host. OS-X can host Linux and/or Windows as guest Operating systems by installing Virtual Box. 2. Or on any hardware system that you can control, you need to install a Linux system (Fedora, CentOS Server, Ubuntu, Ubuntu Server). Tasks to Be Performed • Write the programs listed (questions from Q1 to Q6), run the program examples, and try to answer the questions. Reference for the Assignment Some useful shell commands for process control Command Descriptions & When placed at the end of a command, execute that command in the background. Interrupt and stop the currently running process program. The program remains CTRL + "Z" stopped and waiting in the background for you to resume it. Bring a command in the background to the foreground or resume an interrupted program. fg [%jobnum] If the job number is omitted, the most recently interrupted or background job is put in the foreground. Place an interrupted command into the background. bg [%jobnum] If the job number is omitted, the most recently interrupted job is put in the background. jobs List all background jobs. -

User's Guide and Reference
IBM Compiler and Library for REXX on IBM Z Version 1 Release 4 User’s Guide and Reference IBM SH19-8160-06 Note Before using this information and the product it supports, be sure to read the general information under Appendix G, “Notices,” on page 267. Seventh Edition, August 2013 This edition applies to version 1 release 4 of IBM Compiler for REXX on IBM Z (product number 5695-013) and the IBM Library for REXX on IBM Z (product number 5695-014), and to all subsequent releases and modifications until otherwise indicated in new editions. This edition replaces SH19-8160-04. © Copyright International Business Machines Corporation 1991, 2013. US Government Users Restricted Rights – Use, duplication or disclosure restricted by GSA ADP Schedule Contract with IBM Corp. Contents About This Book..................................................................................................xix How to Read the Syntax Notation............................................................................................................. xix How This Book Is Organized..................................................................................................................... xix How to Send Your Comments.................................................................................................................... xx What's New in Release 4..................................................................................... xxi IBM Compiler for REXX on IBM Z..............................................................................................................xxi -

Lecture 22 Systems Programming Process Control
Lecture 22 Systems Programming Process Control A process is defined as an instance of a program that is currently running. A uni processor system can still execute multiple processes giving the appearance of a multi- processor machine. A call to a program spawns a process. If a mail program is called by n users then n processes or instances are created and executed by the unix system. Many operating systems including windows and unix executes many processes at the same time. When a program is called, a process is created and a process ID is issued. The process ID is given by the function getpid() defined in <unistd.h>. The prototype for pid( ) is given by #include < unistd.h > pid_t getpid(void); In a uni-processor machine, each process takes turns running and for a short duration, a process takes time interval called a timeslice. The unix command ps can be used to list all current process status. ps PID TTY TIME CMD 10150 pts/16 00:00:00 csh 31462 pts/16 00:00:00 ps The command ps lists the process ID (PID), the terminal name(TTY), the amount of time the process has used so far(TIME) and the command it is executing(CMD). Ps command only displays the current user processes. But we can get all the processes with the flag (- a) and in long format with flag (-l) ps –a ps -l ps -al Information provided by each process may include the following. PID The process ID in integer form PPID The parent process ID in integer form STAT The state of the process TIME CPU time used by the process (in seconds) TT Control terminal of the process COMMAND The user command that started the process Copyright @ 2008 Ananda Gunawardena Each process has a process ID that can be obtained using the getpid() a system call declared in unistd.h. -
Bash Redirections Cheat Sheet
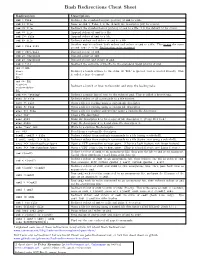
Bash Redirections Cheat Sheet Redirection Description cmd > file Redirect the standard output (stdout) of cmd to a file. cmd 1> file Same as cmd > file. 1 is the default file descriptor (fd) for stdout. cmd 2> file Redirect the standard error (stderr) of cmd to a file. 2 is the default fd for stderr. cmd >> file Append stdout of cmd to a file. cmd 2>> file Append stderr of cmd to a file. cmd &> file Redirect stdout and stderr of cmd to a file. Another way to redirect both stdout and stderr of cmd to a file. This is not the same cmd > file 2>&1 as cmd 2>&1 > file. Redirection order matters! cmd > /dev/null Discard stdout of cmd. cmd 2> /dev/null Discard stderr of cmd. cmd &> /dev/null Discard stdout and stderr of cmd. cmd < file Redirect the contents of the file to the standard input (stdin) of cmd. cmd << EOL line1 Redirect a bunch of lines to the stdin. If 'EOL' is quoted, text is treated literally. This line2 is called a here-document. EOL cmd <<- EOL <tab>foo Redirect a bunch of lines to the stdin and strip the leading tabs. <tab><tab>bar EOL cmd <<< "string" Redirect a single line of text to the stdin of cmd. This is called a here-string. exec 2> file Redirect stderr of all commands to a file forever. exec 3< file Open a file for reading using a custom file descriptor. exec 3> file Open a file for writing using a custom file descriptor. exec 3<> file Open a file for reading and writing using a custom file descriptor.