DOCSLIB.ORG

V. Graph Sketching and Max-Min Problems

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
V. Graph Sketching and Max-Min Problems V. Graph Sketching and Max-Min Problems The signs of the first and second derivatives of a function tell us something about the shape of its graph. In this chapter we learn how to find that information. 30. Tangent and Normal lines to a graph The slope of the tangent the tangent to the graph of f at the point (a, f(a)) is (29) m = f 0(a) and hence the equation for the tangent is (30) y = f(a) + f 0(a)(x − a). The slope of the normal line to the graph is −1/m and thus one could write the equation for the normal as x − a (31) y = f(a) − . f 0(a) When f 0(a) = 0 the tangent is horizontal, and hence the normal is vertical. In this case the equation for the normal cannot be written as in (31), but instead one gets the simpler equation y = f(a). Both cases are covered by this form of the equation for the normal (32) x = a + f 0(a)(f(a) − y). Both (32) and (31) are formulas that you shouldn’t try to remember. It is easier to remember that if the slope of the tangent is m = f 0(a), then the slope of the normal is −1/m. y m 1 = m/ m /run= rise rise 1 / run= −1 − 1 /m m x Figure 14. Why the slope of the normal is −1/(the slope of the tangent). 75 76 31. The intermediate value theorem You could say that a function is continuous if you can draw its graph with out taking your pencil off the paper. A more precise version is the intermediate value theorem: Theorem 31.1. If f is a continuous function on an interval a ≤ x ≤ b, and if y is some number between f(a) and f(b), then there is a number c with a ≤ c ≤ b such that f(c) = y. Here “y between f(a) and f(b)” means that f(a) ≤ y ≤ f(b) if f(a) ≤ f(b), and f(b) ≤ y ≤ f(a) if f(b) ≤ f(a). Example – Square root of 2 Consider the function f(x) = x2. Since f(1) < 2 and f(2) = 4 > 2 the intermediate value theorem with a = 1, b = 2, y = 2 tells us that there is a number c between 1 and 2 such that f(c) = 2, i.e. for which c2 = 2. So the theorem tells us that the square root of 2 exists. π Example – The equation θ + sin θ = 2 Consider the function f(x) = x + sin x. It is a continuous function at all x, so from f(0) = 0 and f(π) = π it follows that there is a number θ between 0 and π such that f(θ) = π/2. In other words, the equation π (33) θ + sin θ = 2 has a solution√ θ with 0 ≤ θ ≤ π/2. Unlike the previous example, where we knew the solution was 2, there is no simple formula for the solution to (33). Example – Solving 1/x = 0 If we apply the intermediate value theorem to the function f(x) = 1/x on the interval [a, b] = [−1, 1], then we see that for any y between f(a) = f(−1) = −1 and f(b) = f(1) = 1 there is a number c in the interval [−1, 1] such that 1/c = y. For instance, we could choose y = 0 (that’s between −1 and +1), and conclude that there is some c with −1 ≤ c ≤ 1 and 1/c = 0. But there is no such c, because 1/c is never zero! So we have done something wrong, and the mistake we made is that we overlooked that our function f(x) = 1/x is not defined on the whole interval −1 ≤ x ≤ 1 because it is not defined at x = 0. The moral: always check the hypotheses of a theorem before you use it! 32. Finding sign changes of a function The intermediate value theorem implies the following very useful fact. Theorem 32.1. If f is continuous function on some interval a < x < b, and if f(x) 6= 0 for all x in this interval, then f(x) is either positive for all a < x < b or else it is negative for all a < x < b. Proof. The theorem says that there can’t be two numbers a < x1 < x2 < b such that f(x1) and f(x2) have opposite signs. If there were two such numbers then the intermediate value theorem would imply that somewhere between x1 and x2 there was a c with f(c) = 0. But we are assuming that f(c) 6= 0 whenever a < c < b. 77 32.1. Example Consider f(x) = (x − 3)(x − 1)2(2x + 1)3. The zeros of f (i.e. the solutions of f(x) = 0) are 1 − , 1, 3. 2 Theorem 32.1 tells us that f(x) must have the same sign for all x between these zeros. We can find those signs by computing f(x) for one x from each interval between two consecutive zeros. We find 2 3 1 f(−1) = (−4)(−2) (−3) > 0 =⇒ f(x) > 0 for x < − 2 2 3 1 f(0) = (−3)(−1) (1) < 0 =⇒ f(x) < 0 for − 2 < x < 1 f(2) = (−1)(1)2(5)3 < 0 =⇒ f(x) < 0 for 1 < x < 3 f(4) = (1)(3)2(9)3 > 0 =⇒ f(x) > 0 for x > 3. When the given function is factored into simple functions, as in this example, there is a different way of finding out where f is positive, and where f is negative. For each of the factors x − 3, (x − 1)2 and (2x + 1)3 it is easy to determine the sign, for any given x. These signs can only change at a zero of the factor. Thus we have • x − 3 is positive for x > 3 and negative for x < 3; • (x − 1)2 is always positive (except at x = 1); 3 1 1 • (2x + 1) is positive for x > − 2 and negative for x < − 2 . Multiplying these signs we get the same conclusions as above. We can summarize this computation in the following diagram: − − − − − − − − −+ + x−3 +++++ ++++++ 2 (x−1) − − + + + + + + + + + 3 (2x+1) + + − − − − − − − + + + f(x) −1/21 3 33. Increasing and decreasing functions Here are four very similar definitions – look closely to see how they differ. • A function is called increasing if a < b implies f(a) < f(b) for all numbers a and b in the domain of f. • A function is called decreasing if a < b implies f(a) > f(b) for all numbers a and b in the domain of f. • The function f is called non-increasing if a < b implies f(a) ≤ f(b) for all numbers a and b in the domain of f. • The function f is called non-decreasing if a < b implies f(b) ≥ f(b) for all numbers a and b in the domain of f. 78 You can summarize these definitions as follows: f is . if for all a and b one has. Increasing: a < b =⇒ f(a) < f(b) Decreasing: a < b =⇒ f(a) > f(b) Non-increasing: a < b =⇒ f(a) ≥ f(b) Non-decreasing: a < b =⇒ f(a) ≤ f(b) The sign of the derivaitve of f tells you if f is increasing or not. More precisely: Theorem 33.1. If a function is non-decreasing on an interval a < x < b then f 0(x) ≥ 0 for all x in that interval. If a function is non-increasing on an interval a < x < b then f 0(x) ≤ 0 for all x in that interval. For instance, if f is non-decreasing, then for any given x and any positive ∆x one has f(x + ∆x) ≥ f(x) and hence f(x + ∆x) − f(x) ≥ 0. ∆x now let ∆x & 0 and you find that f(x + ∆x) − f(x) f 0(x) = lim ≥ 0. ∆x&0 ∆x What about the converse, i.e. if you know the sign of f 0 then what can you say about f? For this we have the following Theorem 33.2. Suppose f is a differentiable function on an interval (a, b). If f 0(x) > 0 for all a < x < b, then f is increasing. If f 0(x) < 0 for all a < x < b, then f is decreasing. a bc Figure 15. According to the Mean Value Theorem there always is some number c between a and b such that the tangent to the graph of f is parallel to the line segment connecting the two points (a, f(a)) and (b, f(b)). This is true for any choice of a and b; c depends on a and b of course. 79 The proof is based on the Mean Value theorem which also finds use in many other situations: Theorem 33.3 (The Mean Value Theorem). If f is a differentiable function on the interval a ≤ x ≤ b, then there is some number c, with a < c < b such that f(b) − f(a) f 0(c) = . b − a Proof of theorem 33.2. We show that f 0(x) > 0 for all x implies that f is increasing. Let x1 < x2 be two numbers between a and b. Then the Mean Value Theorem implies that there is some c between x1 and x2 such that f(x ) − f(x ) f 0(c) = 2 1 , x2 − x1 or 0 f(x2) − f(x1) = f (c)(x2 − x1).
Load more

Recommended publications
  • Plotting, Derivatives, and Integrals for Teaching Calculus in R
    Plotting, Derivatives, and Integrals for Teaching Calculus in R Daniel Kaplan, Cecylia Bocovich, & Randall Pruim July 3, 2012 The mosaic package provides a command notation in R designed to make it easier to teach and to learn introductory calculus, statistics, and modeling. The principle behind mosaic is that a notation can more effectively support learning when it draws clear connections between related concepts, when it is concise and consistent, and when it suppresses extraneous form. At the same time, the notation needs to mesh clearly with R, facilitating students' moving on from the basics to more advanced or individualized work with R. This document describes the calculus-related features of mosaic. As they have developed histori- cally, and for the main as they are taught today, calculus instruction has little or nothing to do with statistics. Calculus software is generally associated with computer algebra systems (CAS) such as Mathematica, which provide the ability to carry out the operations of differentiation, integration, and solving algebraic expressions. The mosaic package provides functions implementing he core operations of calculus | differen- tiation and integration | as well plotting, modeling, fitting, interpolating, smoothing, solving, etc. The notation is designed to emphasize the roles of different kinds of mathematical objects | vari- ables, functions, parameters, data | without unnecessarily turning one into another. For example, the derivative of a function in mosaic, as in mathematics, is itself a function. The result of fitting a functional form to data is similarly a function, not a set of numbers. Traditionally, the calculus curriculum has emphasized symbolic algorithms and rules (such as xn ! nxn−1 and sin(x) ! cos(x)).
    [Show full text]
  • Tutorial 8: Solutions
    Tutorial 8: Solutions Applications of the Derivative 1. We are asked to find the absolute maximum and minimum values of f on the given interval, and state where those values occur: (a) f(x) = 2x3 + 3x2 12x on [1; 4]. − The absolute extrema occur either at a critical point (stationary point or point of non-differentiability) or at the endpoints. The stationary points are given by f 0(x) = 0, which in this case gives 6x2 + 6x 12 = 0 = x = 1; x = 2: − ) − Checking the values at the critical points (only x = 1 is in the interval [1; 4]) and endpoints: f(1) = 7; f(4) = 128: − Therefore the absolute maximum occurs at x = 4 and is given by f(4) = 124 and the absolute minimum occurs at x = 1 and is given by f(1) = 7. − (b) f(x) = (x2 + x)2=3 on [ 2; 3] − As before, we find the critical points. The derivative is given by 2 2x + 1 f 0(x) = 3 (x2 + x)1=2 and hence we have a stationary point when 2x + 1 = 0 and points of non- differentiability whenever x2 + x = 0. Solving these, we get the three critical points, x = 1=2; and x = 0; 1: − − Checking the value of the function at these critical points and the endpoints: f( 2) = 22=3; f( 1) = 0; f( 1=2) = 2−4=3; f(0) = 0; f(3) = (12)2=3: − − − Hence the absolute minimum occurs at either x = 1 or x = 0 since in both − these cases the minimum value is 0, while the absolute maximum occurs at x = 3 and is f(3) = (12)2=3.
    [Show full text]
  • Lecture Notes – 1
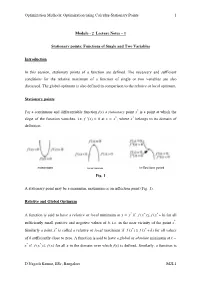
    Optimization Methods: Optimization using Calculus-Stationary Points 1 Module - 2 Lecture Notes – 1 Stationary points: Functions of Single and Two Variables Introduction In this session, stationary points of a function are defined. The necessary and sufficient conditions for the relative maximum of a function of single or two variables are also discussed. The global optimum is also defined in comparison to the relative or local optimum. Stationary points For a continuous and differentiable function f(x) a stationary point x* is a point at which the slope of the function vanishes, i.e. f ’(x) = 0 at x = x*, where x* belongs to its domain of definition. minimum maximum inflection point Fig. 1 A stationary point may be a minimum, maximum or an inflection point (Fig. 1). Relative and Global Optimum A function is said to have a relative or local minimum at x = x* if f ()xfxh**≤+ ( )for all sufficiently small positive and negative values of h, i.e. in the near vicinity of the point x*. Similarly a point x* is called a relative or local maximum if f ()xfxh**≥+ ( )for all values of h sufficiently close to zero. A function is said to have a global or absolute minimum at x = x* if f ()xfx* ≤ ()for all x in the domain over which f(x) is defined. Similarly, a function is D Nagesh Kumar, IISc, Bangalore M2L1 Optimization Methods: Optimization using Calculus-Stationary Points 2 said to have a global or absolute maximum at x = x* if f ()xfx* ≥ ()for all x in the domain over which f(x) is defined.
    [Show full text]
  • Calculus Terminology
    AP Calculus BC Calculus Terminology Absolute Convergence Asymptote Continued Sum Absolute Maximum Average Rate of Change Continuous Function Absolute Minimum Average Value of a Function Continuously Differentiable Function Absolutely Convergent Axis of Rotation Converge Acceleration Boundary Value Problem Converge Absolutely Alternating Series Bounded Function Converge Conditionally Alternating Series Remainder Bounded Sequence Convergence Tests Alternating Series Test Bounds of Integration Convergent Sequence Analytic Methods Calculus Convergent Series Annulus Cartesian Form Critical Number Antiderivative of a Function Cavalieri’s Principle Critical Point Approximation by Differentials Center of Mass Formula Critical Value Arc Length of a Curve Centroid Curly d Area below a Curve Chain Rule Curve Area between Curves Comparison Test Curve Sketching Area of an Ellipse Concave Cusp Area of a Parabolic Segment Concave Down Cylindrical Shell Method Area under a Curve Concave Up Decreasing Function Area Using Parametric Equations Conditional Convergence Definite Integral Area Using Polar Coordinates Constant Term Definite Integral Rules Degenerate Divergent Series Function Operations Del Operator e Fundamental Theorem of Calculus Deleted Neighborhood Ellipsoid GLB Derivative End Behavior Global Maximum Derivative of a Power Series Essential Discontinuity Global Minimum Derivative Rules Explicit Differentiation Golden Spiral Difference Quotient Explicit Function Graphic Methods Differentiable Exponential Decay Greatest Lower Bound Differential
    [Show full text]
  • The Theory of Stationary Point Processes By
    THE THEORY OF STATIONARY POINT PROCESSES BY FREDERICK J. BEUTLER and OSCAR A. Z. LENEMAN (1) The University of Michigan, Ann Arbor, Michigan, U.S.A. (3) Table of contents Abstract .................................... 159 1.0. Introduction and Summary ......................... 160 2.0. Stationarity properties for point processes ................... 161 2.1. Forward recurrence times and points in an interval ............. 163 2.2. Backward recurrence times and stationarity ................ 167 2.3. Equivalent stationarity conditions .................... 170 3.0. Distribution functions, moments, and sample averages of the s.p.p ......... 172 3.1. Convexity and absolute continuity .................... 172 3.2. Existence and global properties of moments ................ 174 3.3. First and second moments ........................ 176 3.4. Interval statistics and the computation of moments ............ 178 3.5. Distribution of the t n .......................... 182 3.6. An ergodic theorem ........................... 184 4.0. Classes and examples of stationary point processes ............... 185 4.1. Poisson processes ............................ 186 4.2. Periodic processes ........................... 187 4.3. Compound processes .......................... 189 4.4. The generalized skip process ....................... 189 4.5. Jitte processes ............................ 192 4.6. ~deprendent identically distributed intervals ................ 193 Acknowledgments ............................... 196 References ................................... 196 Abstract An axiomatic formulation is presented for point processes which may be interpreted as ordered sequences of points randomly located on the real line. Such concepts as forward recurrence times and number of points in intervals are defined and related in set-theoretic Q) Presently at Massachusetts Institute of Technology, Lexington, Mass., U.S.A. (2) This work was supported by the National Aeronautics and Space Administration under research grant NsG-2-59. 11 - 662901. Aeta mathematica. 116. Imprlm$ le 19 septembre 1966.
    [Show full text]
  • The First Derivative and Stationary Points
    Mathematics Learning Centre The first derivative and stationary points Jackie Nicholas c 2004 University of Sydney Mathematics Learning Centre, University of Sydney 1 The first derivative and stationary points dy The derivative of a function y = f(x) tell us a lot about the shape of a curve. In this dx section we will discuss the concepts of stationary points and increasing and decreasing functions. However, we will limit our discussion to functions y = f(x) which are well behaved. Certain functions cause technical difficulties so we will concentrate on those that don’t! The first derivative dy The derivative, dx ,isthe slope of the tangent to the curve y = f(x)atthe point x.Ifwe know about the derivative we can deduce a lot about the curve itself. Increasing functions dy If > 0 for all values of x in an interval I, then we know that the slope of the tangent dx to the curve is positive for all values of x in I and so the function y = f(x)isincreasing on the interval I. 3 For example, let y = x + x, then y dy 1 =3x2 +1> 0 for all values of x. dx That is, the slope of the tangent to the x curve is positive for all values of x. So, –1 0 1 y = x3 + x is an increasing function for all values of x. –1 The graph of y = x3 + x. We know that the function y = x2 is increasing for x>0. We can work this out from the derivative. 2 If y = x then y dy 2 =2x>0 for all x>0.
    [Show full text]
  • EE2 Maths: Stationary Points
    EE2 Maths: Stationary Points df Univariate case: When we maximize f(x) (solving for the x0 such that dx = 0) the d df gradient is zero at these points. What about the rate of change of gradient: dx ( dx ) at the minimum x0? For a minimum the gradient increases as x0 ! x0 + ∆x (∆x > 0). It follows d2f d2f that dx2 > 0. The opposite is true for a maximum: dx2 < 0, the gradient decreases upon d2f positive steps away from x0. For a point of inflection dx2 = 0. r @f @f Multivariate case: Stationary points occur when f = 0. In 2-d this is ( @x ; @y ) = 0, @f @f namely, a generalization of the univariate case. Recall that df = @x dx + @y dy can be written as df = ds · rf where ds = (dx; dy). If rf = 0 at (x0; y0) then any infinitesimal step ds away from (x0; y0) will still leave f unchanged, i.e. df = 0. There are three types of stationary points of f(x; y): Maxima, Minima and Saddle Points. We'll draw some of their properties on the board. We will now attempt to find ways of identifying the character of each of the stationary points of f(x; y). Consider a Taylor expansion about a stationary point (x0; y0). We know that rf = 0 at (x0; y0) so writing (∆x; ∆y) = (x − x0; y − y0) we find: − ∆f = f(x; y)[ f(x0; y0) ] 1 @2f @2f @2f ' 0 + (∆x)2 + 2 ∆x∆y + (∆y)2 : (1) 2! @x2 @x@y @y2 Maxima: At a maximum all small steps away from (x0; y0) lead to ∆f < 0.
    [Show full text]
  • 5 Graph Theory
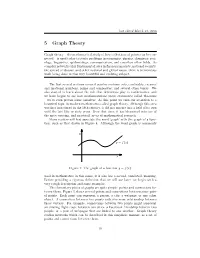
    last edited March 21, 2016 5 Graph Theory Graph theory – the mathematical study of how collections of points can be con- nected – is used today to study problems in economics, physics, chemistry, soci- ology, linguistics, epidemiology, communication, and countless other fields. As complex networks play fundamental roles in financial markets, national security, the spread of disease, and other national and global issues, there is tremendous work being done in this very beautiful and evolving subject. The first several sections covered number systems, sets, cardinality, rational and irrational numbers, prime and composites, and several other topics. We also started to learn about the role that definitions play in mathematics, and we have begun to see how mathematicians prove statements called theorems – we’ve even proven some ourselves. At this point we turn our attention to a beautiful topic in modern mathematics called graph theory. Although this area was first introduced in the 18th century, it did not mature into a field of its own until the last fifty or sixty years. Over that time, it has blossomed into one of the most exciting, and practical, areas of mathematical research. Many readers will first associate the word ‘graph’ with the graph of a func- tion, such as that drawn in Figure 4. Although the word graph is commonly Figure 4: The graph of a function y = f(x). used in mathematics in this sense, it is also has a second, unrelated, meaning. Before providing a rigorous definition that we will use later, we begin with a very rough description and some examples.
    [Show full text]
  • Lecture 11: Graphs of Functions Definition If F Is a Function With
    Lecture 11: Graphs of Functions Definition If f is a function with domain A, then the graph of f is the set of all ordered pairs f(x; f(x))jx 2 Ag; that is, the graph of f is the set of all points (x; y) such that y = f(x). This is the same as the graph of the equation y = f(x), discussed in the lecture on Cartesian co-ordinates. The graph of a function allows us to translate between algebra and pictures or geometry. A function of the form f(x) = mx+b is called a linear function because the graph of the corresponding equation y = mx + b is a line. A function of the form f(x) = c where c is a real number (a constant) is called a constant function since its value does not vary as x varies. Example Draw the graphs of the functions: f(x) = 2; g(x) = 2x + 1: Graphing functions As you progress through calculus, your ability to picture the graph of a function will increase using sophisticated tools such as limits and derivatives. The most basic method of getting a picture of the graph of a function is to use the join-the-dots method. Basically, you pick a few values of x and calculate the corresponding values of y or f(x), plot the resulting points f(x; f(x)g and join the dots. Example Fill in the tables shown below for the functions p f(x) = x2; g(x) = x3; h(x) = x and plot the corresponding points on the Cartesian plane.
    [Show full text]
  • Maximum and Minimum Definition
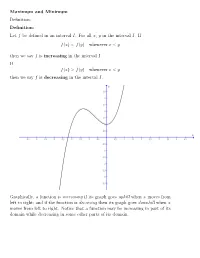
    Maximum and Minimum Definition: Definition: Let f be defined in an interval I. For all x, y in the interval I. If f(x) < f(y) whenever x < y then we say f is increasing in the interval I. If f(x) > f(y) whenever x < y then we say f is decreasing in the interval I. Graphically, a function is increasing if its graph goes uphill when x moves from left to right; and if the function is decresing then its graph goes downhill when x moves from left to right. Notice that a function may be increasing in part of its domain while decreasing in some other parts of its domain. For example, consider f(x) = x2. Notice that the graph of f goes downhill before x = 0 and it goes uphill after x = 0. So f(x) = x2 is decreasing on the interval (−∞; 0) and increasing on the interval (0; 1). Consider f(x) = sin x. π π 3π 5π 7π 9π f is increasing on the intervals (− 2 ; 2 ), ( 2 ; 2 ), ( 2 ; 2 )...etc, while it is de- π 3π 5π 7π 9π 11π creasing on the intervals ( 2 ; 2 ), ( 2 ; 2 ), ( 2 ; 2 )...etc. In general, f = sin x is (2n+1)π (2n+3)π increasing on any interval of the form ( 2 ; 2 ), where n is an odd integer. (2m+1)π (2m+3)π f(x) = sin x is decreasing on any interval of the form ( 2 ; 2 ), where m is an even integer. What about a constant function? Is a constant function an increasing function or decreasing function? Well, it is like asking when you walking on a flat road, as you going uphill or downhill? From our definition, a constant function is neither increasing nor decreasing.
    [Show full text]
  • Chapter 3. Linearization and Gradient Equation Fx(X, Y) = Fxx(X, Y)
    Oliver Knill, Harvard Summer School, 2010 An equation for an unknown function f(x, y) which involves partial derivatives with respect to at least two variables is called a partial differential equation. If only the derivative with respect to one variable appears, it is called an ordinary differential equation. Examples of partial differential equations are the wave equation fxx(x, y) = fyy(x, y) and the heat Chapter 3. Linearization and Gradient equation fx(x, y) = fxx(x, y). An other example is the Laplace equation fxx + fyy = 0 or the advection equation ft = fx. Paul Dirac once said: ”A great deal of my work is just playing with equations and see- Section 3.1: Partial derivatives and partial differential equations ing what they give. I don’t suppose that applies so much to other physicists; I think it’s a peculiarity of myself that I like to play about with equations, just looking for beautiful ∂ mathematical relations If f(x, y) is a function of two variables, then ∂x f(x, y) is defined as the derivative of the function which maybe don’t have any physical meaning at all. Sometimes g(x) = f(x, y), where y is considered a constant. It is called partial derivative of f with they do.” Dirac discovered a PDE describing the electron which is consistent both with quan- respect to x. The partial derivative with respect to y is defined similarly. tum theory and special relativity. This won him the Nobel Prize in 1933. Dirac’s equation could have two solutions, one for an electron with positive energy, and one for an electron with ∂ antiparticle One also uses the short hand notation fx(x, y)= ∂x f(x, y).
    [Show full text]
  • Applications of Differentiation Applications of Differentiation– a Guide for Teachers (Years 11–12)
    1 Supporting Australian Mathematics Project 2 3 4 5 6 12 11 7 10 8 9 A guide for teachers – Years 11 and 12 Calculus: Module 12 Applications of differentiation Applications of differentiation – A guide for teachers (Years 11–12) Principal author: Dr Michael Evans, AMSI Peter Brown, University of NSW Associate Professor David Hunt, University of NSW Dr Daniel Mathews, Monash University Editor: Dr Jane Pitkethly, La Trobe University Illustrations and web design: Catherine Tan, Michael Shaw Full bibliographic details are available from Education Services Australia. Published by Education Services Australia PO Box 177 Carlton South Vic 3053 Australia Tel: (03) 9207 9600 Fax: (03) 9910 9800 Email: [email protected] Website: www.esa.edu.au © 2013 Education Services Australia Ltd, except where indicated otherwise. You may copy, distribute and adapt this material free of charge for non-commercial educational purposes, provided you retain all copyright notices and acknowledgements. This publication is funded by the Australian Government Department of Education, Employment and Workplace Relations. Supporting Australian Mathematics Project Australian Mathematical Sciences Institute Building 161 The University of Melbourne VIC 3010 Email: [email protected] Website: www.amsi.org.au Assumed knowledge ..................................... 4 Motivation ........................................... 4 Content ............................................. 5 Graph sketching ....................................... 5 More graph sketching ..................................
    [Show full text]