DOCSLIB.ORG

Chapter 0 0-2 Chapter 0 Mathematical Background CS 341: Foundations of CS II Contents • Overview of Course • Alphabets, Strings, and Languages Marvin K

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Chapter 0 0-2 Chapter 0 Mathematical Background CS 341: Foundations of CS II Contents • Overview of Course • Alphabets, Strings, and Languages Marvin K CS 341: Chapter 0 0-2 Chapter 0 Mathematical Background CS 341: Foundations of CS II Contents • Overview of course • Alphabets, Strings, and Languages Marvin K. Nakayama • Set Relations and Operations Computer Science Department • Functions and Operations New Jersey Institute of Technology Newark, NJ 07102 • Graphs • Boolean Logic CS 341: Chapter 0 0-3 CS 341: Chapter 0 0-4 Overview of Course Automata Theory • Finite automata and regular expressions • Automata Theory: String matching (grep in Unix) What is a computer? Circuit design • Computability Theory Communication protocols What can and cannot be computed? • Context-free grammars and pushdown automata Compilers • Complexity Theory Programming languages What can and cannot be computed efficiently? • Turing machines Computers Algorithms • Why study different models of computation? CS 341: Chapter 0 0-5 CS 341: Chapter 0 0-6 Computability Theory Complexity Theory • For a solvable problem, is there an efficient algorithm to solve it? • There are algorithms to solve many problems. • Some problems can be solved efficiently: • But there are some problems for which there is no algorithm. Is there a path from A to H with total cost at most 20? 11 • F These are called undecidable problems: 6 6 B 5 edge labels are costs 6 D Does a program run forever? 3 8 A 2 H Is a program correct? 2 6 C E 6 Are two programs equivalent? 5 16 G • Some problems have no known efficient algorithm: Is there a path from A to H with total cost at least 50? CS 341: Chapter 0 0-7 CS 341: Chapter 0 0-8 Alphabets, Strings, and Languages Sets Definition: A set is an unordered collection of objects or elements. Examples: • Sets are written with curly braces {}. • The set {a, b, c} has elements a, b,andc. • The elements in the set are written within the curly braces. • The sets {a, b, c} and {b, c, b, a, a} are the same. Order and redundancy do not matter in a set. Definition: • The set {a} has element a. • For any set S,“x ∈ S” denotes that x is an element of the set S. {a} and a are different things. • Also, “y ∈ S” denotes that y is not an element of the set S. {a} is a set with one element a. Remark: We often specify a set using set notation, e.g., • The set Z of integers is { | ∈R 2 − 4=0} x x ,x {...,−2, −1, 0, 1, 2,...}. •R denotes the set of real numbers. • The set Z+ of nonnegative integers is • | “ ” means “such that” {0, 1, 2, 3,...}. • Comma means “and” CS 341: Chapter 0 0-9 CS 341: Chapter 0 0-10 Sets Alphabets Examples: An alphabet is a finite set of fundamental units (called letters or symbols). • The set of even numbers is {0, 2, 4, 6, 8, 10, 12,...}, Remark: We typically denote an alphabet by a capital Greek letter { 2 | =0 1 2 } which we can also write as n n , , ,... • e.g., Σ or Γ (i.e., Sigma or Gamma) In particular, 0 is an even number. • The set of positive even numbers is Examples: {2, 4, 6, 8, 10, 12,...} • The alphabet of lower-case Roman letters is • The set of odd numbers Σ={ a, b, c,...,z }. {1, 3, 5, 7, 9, 11, 13,...} There are 26 lower-case Roman letters. can also be written as { 2n +1| n =0, 1, 2,...}. • The alphabet of upper-case Roman letters is Γ={ A, B, C,...,Z }. Example: If A is the set { 2n | n =0, 1, 2,...}, then 4 ∈ A, but 5 ∈ A. There are 26 upper-case Roman letters. CS 341: Chapter 0 0-11 CS 341: Chapter 0 0-12 Alphabets Sequences and Strings Definition: Sequence of objects is a list of these objects in some order. • The alphabet of Arabic numerals is • Σ={ 0, 1, 2,...,9 }. Order and redundancy matter in a sequence, unlike in a set. • There are 10 Arabic numerals. a, b, c and b, c, b, a, a are different sequences. •{a, b, c} and {b, c, b, a, a} are the same set. • In this class we will often use the alphabets Definition: A string over an alphabet is a finite sequence of Σ={a, b}, symbols from the alphabet (written without commas or spaces between Σ={0 1} , . the symbols). Examples: • x, cromulent, embiggen,andkwyjibo are strings over the alphabet Σ={a,b,c,...,z}. • 0131 is a string over the alphabet Σ={0, 1, 2,...,9}. CS 341: Chapter 0 0-13 CS 341: Chapter 0 0-14 String Length Kleene Star ∗ Definition: The length of a string w is the number of symbols in w. Definition: For a given alphabet Σ,letΣ denote the set of all possible strings (including ε)overΣ. • Sometimes denote length of w by length(w) or |w|. Example: If Σ={a, b},then ( )=| | =3 ∗ Example: length mom mom . Σ = { ε, a, b, aa, ab, ba, bb, aaa, aab, aba, abb, . }. Definition: The empty string or null string, denoted by ε (i.e., epsilon), is the string consisting of no symbols, i.e., |ε| =0. CS 341: Chapter 0 0-15 CS 341: Chapter 0 0-16 String Ordering Concatenation Definition: A list of strings w1,w2,... over an alphabet Σ is in Definition: The concatenation of strings x and y is the string xy. string order (also called shortlex order)if 1. shorter strings always appear before longer strings, and Examples: 2. strings of the same length appear in alphabetical order. • If x = cat and y = dog,thenxy = catdog and yx = dogcat. • = = = = ∗ If x ε and y ab,thenxy ab yx. Example: If Σ={0, 1}, the string ordering of the strings in Σ is ε, 0, 1, 00, 01, 10, 11, 000, 001, 010, 011,... • If x = ε and y = ε,thenxy = ε = yx; i.e., εε = ε. Remarks: • Previous editions (before the 3rd) of Sipser’s book instead called this lexicographic order. • String ordering is not the same as dictionary ordering. Why? CS 341: Chapter 0 0-17 CS 341: Chapter 0 0-18 Substring Definition: For string w,wedefinewn for n ≥ 0 inductively as • 0 = w ε; Definition: A substring of a string w is any contiguous part of w. −1 • wn = wn w for any n ≥ 1. • i.e., y is a substring of w if there exist strings x and z (eitherorboth possibly empty) such that w = xyz. Example: If w = dog,then 0 w = ε, 1 0 Examples: w = w w = εdog = dog, 2 1 • =47 = 472 = =2 w = w w = dogdog, y is a substring of w since letting x ε and z 3 2 gives w = xyz. w = w w = dogdogdog, • 472 4 7 2 47 72 472 . The string has substrings ε, , , , , ,and . • 42 is not a substring of 472. Example: Can also apply this to a single symbol 3 • a = aaa 0 • a = ε. CS 341: Chapter 0 0-19 CS 341: Chapter 0 0-20 Languages Examples of Languages Definition: A (formal) language is a set of strings over an alphabet. Example: Alphabet Σ={a}. • Language typically denoted by capital Roman letter, e.g., A, B,orL. Language = { } Examples: L0 ε, a, aa, aaa, aaaa, . = { an | n =0, 1, 2, 3 ...} • Computer languages, e.g., C, C++, or Java, are languages with alphabet Note that 0 Σ={ a, b,...,z, A, B,...,Z,,0, 1, 2,...,9, , • a = ε,soε ∈ L0. >, <, =, +, -, *, /, (, ), ., ,, &, !, %, |, ’, ", • there are different ways we can specify a language. :, ;,ˆ, {, }, @, #, \, ?, $, ~, ‘, CR, FF}. Another language The rules of syntax define the rules for the language. L1 = { an | n ≥ 1 } • The set of valid variable names in C++ is a language. What are the has ε ∈ L1. alphabet and rules defining valid variable names in C++? CS 341: Chapter 0 0-21 CS 341: Chapter 0 0-22 Examples of Languages Examples of Languages Example: Alphabet Σ={a}. Example: Let Σ={a, b}, and we can define a language L consisting Language of all strings that begin with a followed by zero or more b’s; i.e., L2 = { a, aaa, aaaaa, aaaaaaa, . } L = { a, ab, abb, abbb, . } 2 +1 = { a n | n =0, 1, 2, 3,...} = { abn | n =0, 1, 2,...}. Is L the language of strings beginning with a? Example: Alphabet Σ={0, 1, 2,...,9}. Language Definition: The set ∅, which is called the empty set,istheset L3 = { any string of symbols that does not start with symbol “0”} consisting of no elements. = { ε, 1, 2, 3,...,9, 10, 11,...} Remarks: • ε ∈∅since ∅ has no elements. •∅= { ε } since ∅ has no elements. CS 341: Chapter 0 0-23 CS 341: Chapter 0 0-24 Set Relations and Operations Equal Sets Definition: If S and T are sets, then S ⊆ T (S is a subset of T )if Definition: Two sets S and T are equal, written S = T ,if x ∈ S implies that x ∈ T . S ⊆ T and T ⊆ S. • Each element of S is also an element of T . Examples: Examples: • Suppose S = { ab, ba } and T = { ba, ab }. • Suppose S = { ab, ba } and T = { ab, ba, aaa }. Then S ⊆ T and T ⊆ S. ⊆ Then S T . So S = T . But T ⊆ S. • Suppose S = { ab, ba } and T = { ba, ab, aaa }. • Suppose S = { ba, ab } and T = { aa, ba }. Then S ⊆ T , but T ⊆ S. ⊆ ⊆ Then S T and T S. So S = T . CS 341: Chapter 0 0-25 CS 341: Chapter 0 0-26 Union Intersection Definition: The union of two sets S and T is Definition: The intersection of two sets S and T is S ∪ T = { x | x ∈ S or x ∈ T } S ∩ T = { x | x ∈ S and x ∈ T }, • S ∪ T consists of all elements in S or in T (or in both).
Load more

Recommended publications
  • Metaobject Protocols: Why We Want Them and What Else They Can Do
    Metaobject protocols: Why we want them and what else they can do Gregor Kiczales, J.Michael Ashley, Luis Rodriguez, Amin Vahdat, and Daniel G. Bobrow Published in A. Paepcke, editor, Object-Oriented Programming: The CLOS Perspective, pages 101 ¾ 118. The MIT Press, Cambridge, MA, 1993. © Massachusetts Institute of Technology All rights reserved. No part of this book may be reproduced in any form by any electronic or mechanical means (including photocopying, recording, or information storage and retrieval) without permission in writing from the publisher. Metaob ject Proto cols WhyWeWant Them and What Else They Can Do App ears in Object OrientedProgramming: The CLOS Perspective c Copyright 1993 MIT Press Gregor Kiczales, J. Michael Ashley, Luis Ro driguez, Amin Vahdat and Daniel G. Bobrow Original ly conceivedasaneat idea that could help solve problems in the design and implementation of CLOS, the metaobject protocol framework now appears to have applicability to a wide range of problems that come up in high-level languages. This chapter sketches this wider potential, by drawing an analogy to ordinary language design, by presenting some early design principles, and by presenting an overview of three new metaobject protcols we have designed that, respectively, control the semantics of Scheme, the compilation of Scheme, and the static paral lelization of Scheme programs. Intro duction The CLOS Metaob ject Proto col MOP was motivated by the tension b etween, what at the time, seemed liketwo con icting desires. The rst was to have a relatively small but p owerful language for doing ob ject-oriented programming in Lisp. The second was to satisfy what seemed to b e a large numb er of user demands, including: compatibility with previous languages, p erformance compara- ble to or b etter than previous implementations and extensibility to allow further exp erimentation with ob ject-oriented concepts see Chapter 2 for examples of directions in which ob ject-oriented techniques might b e pushed.
    [Show full text]
  • C Strings and Pointers
    Software Design Lecture Notes Prof. Stewart Weiss C Strings and Pointers C Strings and Pointers Motivation The C++ string class makes it easy to create and manipulate string data, and is a good thing to learn when rst starting to program in C++ because it allows you to work with string data without understanding much about why it works or what goes on behind the scenes. You can declare and initialize strings, read data into them, append to them, get their size, and do other kinds of useful things with them. However, it is at least as important to know how to work with another type of string, the C string. The C string has its detractors, some of whom have well-founded criticism of it. But much of the negative image of the maligned C string comes from its abuse by lazy programmers and hackers. Because C strings are found in so much legacy code, you cannot call yourself a C++ programmer unless you understand them. Even more important, C++'s input/output library is harder to use when it comes to input validation, whereas the C input/output library, which works entirely with C strings, is easy to use, robust, and powerful. In addition, the C++ main() function has, in addition to the prototype int main() the more important prototype int main ( int argc, char* argv[] ) and this latter form is in fact, a prototype whose second argument is an array of C strings. If you ever want to write a program that obtains the command line arguments entered by its user, you need to know how to use C strings.
    [Show full text]
  • 250P: Computer Systems Architecture Lecture 10: Caches
    250P: Computer Systems Architecture Lecture 10: Caches Anton Burtsev April, 2021 The Cache Hierarchy Core L1 L2 L3 Off-chip memory 2 Accessing the Cache Byte address 101000 Offset 8-byte words 8 words: 3 index bits Direct-mapped cache: each address maps to a unique address Sets Data array 3 The Tag Array Byte address 101000 Tag 8-byte words Compare Direct-mapped cache: each address maps to a unique address Tag array Data array 4 Increasing Line Size Byte address A large cache line size smaller tag array, fewer misses because of spatial locality 10100000 32-byte cache Tag Offset line size or block size Tag array Data array 5 Associativity Byte address Set associativity fewer conflicts; wasted power because multiple data and tags are read 10100000 Tag Way-1 Way-2 Tag array Data array Compare 6 Example • 32 KB 4-way set-associative data cache array with 32 byte line sizes • How many sets? • How many index bits, offset bits, tag bits? • How large is the tag array? 7 Types of Cache Misses • Compulsory misses: happens the first time a memory word is accessed – the misses for an infinite cache • Capacity misses: happens because the program touched many other words before re-touching the same word – the misses for a fully-associative cache • Conflict misses: happens because two words map to the same location in the cache – the misses generated while moving from a fully-associative to a direct-mapped cache • Sidenote: can a fully-associative cache have more misses than a direct-mapped cache of the same size? 8 Reducing Miss Rate • Large block
    [Show full text]
  • Chapter 2 Basics of Scanning And
    Chapter 2 Basics of Scanning and Conventional Programming in Java In this chapter, we will introduce you to an initial set of Java features, the equivalent of which you should have seen in your CS-1 class; the separation of problem, representation, algorithm and program – four concepts you have probably seen in your CS-1 class; style rules with which you are probably familiar, and scanning - a general class of problems we see in both computer science and other fields. Each chapter is associated with an animating recorded PowerPoint presentation and a YouTube video created from the presentation. It is meant to be a transcript of the associated presentation that contains little graphics and thus can be read even on a small device. You should refer to the associated material if you feel the need for a different instruction medium. Also associated with each chapter is hyperlinked code examples presented here. References to previously presented code modules are links that can be traversed to remind you of the details. The resources for this chapter are: PowerPoint Presentation YouTube Video Code Examples Algorithms and Representation Four concepts we explicitly or implicitly encounter while programming are problems, representations, algorithms and programs. Programs, of course, are instructions executed by the computer. Problems are what we try to solve when we write programs. Usually we do not go directly from problems to programs. Two intermediate steps are creating algorithms and identifying representations. Algorithms are sequences of steps to solve problems. So are programs. Thus, all programs are algorithms but the reverse is not true.
    [Show full text]
  • BALANCING the Eulisp METAOBJECT PROTOCOL
    LISP AND SYMBOLIC COMPUTATION An International Journal c Kluwer Academic Publishers Manufactured in The Netherlands Balancing the EuLisp Metaob ject Proto col y HARRY BRETTHAUER bretthauergmdde JURGEN KOPP koppgmdde German National Research Center for Computer Science GMD PO Box W Sankt Augustin FRG HARLEY DAVIS davisilogfr ILOG SA avenue Gal lieni Gentil ly France KEITH PLAYFORD kjpmathsbathacuk School of Mathematical Sciences University of Bath Bath BA AY UK Keywords Ob jectoriented Programming Language Design Abstract The challenge for the metaob ject proto col designer is to balance the con icting demands of eciency simplici ty and extensibil ity It is imp ossible to know all desired extensions in advance some of them will require greater functionality while oth ers require greater eciency In addition the proto col itself must b e suciently simple that it can b e fully do cumented and understo o d by those who need to use it This pap er presents the framework of a metaob ject proto col for EuLisp which provides expressiveness by a multileveled proto col and achieves eciency by static semantics for predened metaob jects and mo dularizin g their op erations The EuLisp mo dule system supp orts global optimizations of metaob ject applicati ons The metaob ject system itself is structured into mo dules taking into account the consequences for the compiler It provides introsp ective op erations as well as extension interfaces for various functionaliti es including new inheritance allo cation and slot access semantics While
    [Show full text]
  • MA/CSSE 473 Day 15 Return Exam
    MA/CSSE 473 Day 15 Return Exam Student questions Towers of Hanoi Subsets Ordered Permutations MA/CSSE 473 Day 13 • Student Questions on exam or anything else •Towers of Hanoi • Subset generation –Gray code • Permutations and order 1 Towers of Hanoi •Move all disks from peg A to peg B •One at a time • Never place larger disk on top of a smaller disk •Demo •Code • Recurrence and solution Towers of Hanoi code Recurrence for number of moves, and its solution? 2 Permutations and order number permutation number permutation •Given a permutation 0 0123 12 2013 of 0, 1, …, n‐1, can 1 0132 13 2031 2 0213 14 2103 we directly find the 3 0231 15 2130 next permutation in 4 0312 16 2301 the lexicographic 5 0321 17 2310 sequence? 6 1023 18 3012 7 1032 19 3021 •Given a permutation 8 1203 20 3102 of 0..n‐1, can we 9 1230 21 3120 determine its 10 1302 22 3201 11 1320 23 3210 permutation sequence number? •Given n and i, can we directly generate the ith permutation of 0, …, n‐1? Subset generation • Goal: generate all subsets of {0, 1, 2, …, N‐1} • Bottom‐up (decrease‐by‐one) approach •First generate Sn‐1, the collection of all subsets of {0, …, N‐2} •Then Sn = Sn‐1 { Sn‐1 {n‐1} : sSn‐1} 3 Subset generation • Numeric approach: Each subset of {0, …, N‐1} corresponds to an bit string of length N where the ith bit is 1 iff i is in the subset. •So each subset can be represented by N bits.
    [Show full text]
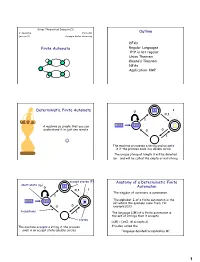
  • Deterministic Finite Automata 0 0,1 1
    Great Theoretical Ideas in CS V. Adamchik CS 15-251 Outline Lecture 21 Carnegie Mellon University DFAs Finite Automata Regular Languages 0n1n is not regular Union Theorem Kleene’s Theorem NFAs Application: KMP 11 1 Deterministic Finite Automata 0 0,1 1 A machine so simple that you can 0111 111 1 ϵ understand it in just one minute 0 0 1 The machine processes a string and accepts it if the process ends in a double circle The unique string of length 0 will be denoted by ε and will be called the empty or null string accept states (F) Anatomy of a Deterministic Finite start state (q0) 11 0 Automaton 0,1 1 The singular of automata is automaton. 1 The alphabet Σ of a finite automaton is the 0111 111 1 ϵ set where the symbols come from, for 0 0 example {0,1} transitions 1 The language L(M) of a finite automaton is the set of strings that it accepts states L(M) = {x∈Σ: M accepts x} The machine accepts a string if the process It’s also called the ends in an accept state (double circle) “language decided/accepted by M”. 1 The Language L(M) of Machine M The Language L(M) of Machine M 0 0 0 0,1 1 q 0 q1 q0 1 1 What language does this DFA decide/accept? L(M) = All strings of 0s and 1s The language of a finite automaton is the set of strings that it accepts L(M) = { w | w has an even number of 1s} M = (Q, Σ, , q0, F) Q = {q0, q1, q2, q3} Formal definition of DFAs where Σ = {0,1} A finite automaton is a 5-tuple M = (Q, Σ, , q0, F) q0 Q is start state Q is the finite set of states F = {q1, q2} Q accept states : Q Σ → Q transition function Σ is the alphabet : Q Σ → Q is the transition function q 1 0 1 0 1 0,1 q0 Q is the start state q0 q0 q1 1 q q1 q2 q2 F Q is the set of accept states 0 M q2 0 0 q2 q3 q2 q q q 1 3 0 2 L(M) = the language of machine M q3 = set of all strings machine M accepts EXAMPLE Determine the language An automaton that accepts all recognized by and only those strings that contain 001 1 0,1 0,1 0 1 0 0 0 1 {0} {00} {001} 1 L(M)={1,11,111, …} 2 Membership problem Determine the language decided by Determine whether some word belongs to the language.
    [Show full text]
  • 1 (15 Points) Lexicosort
    CS161 Homework 2 Due: 22 April 2016, 12 noon Submit on Gradescope Handed out: 15 April 2016 Instructions: Please answer the following questions to the best of your ability. If you are asked to show your work, please include relevant calculations for deriving your answer. If you are asked to explain your answer, give a short (∼ 1 sentence) intuitive description of your answer. If you are asked to prove a result, please write a complete proof at the level of detail and rigor expected in prior CS Theory classes (i.e. 103). When writing proofs, please strive for clarity and brevity (in that order). Cite any sources you reference. 1 (15 points) LexicoSort In class, we learned how to use CountingSort to efficiently sort sequences of values drawn from a set of constant size. In this problem, we will explore how this method lends itself to lexicographic sorting. Let S = `s1s2:::sa' and T = `t1t2:::tb' be strings of length a and b, respectively (we call si the ith letter of S). We say that S is lexicographically less than T , denoting S <lex T , if either • a < b and si = ti for all i = 1; 2; :::; a, or • There exists an index i ≤ min fa; bg such that sj = tj for all j = 1; 2; :::; i − 1 and si < ti. Lexicographic sorting algorithm aims to sort a given set of n strings into lexicographically ascending order (in case of ties due to identical strings, then in non-descending order). For each of the following, describe your algorithm clearly, and analyze its running time and prove cor- rectness.
    [Show full text]
  • Total Ordering on Subgroups and Cosets
    Total Ordering on Subgroups and Cosets ∗ Alexander Hulpke Steve Linton Department of Mathematics Centre for Interdisciplinary Research in Colorado State University Computational Algebra 1874 Campus Delivery University of St Andrews Fort Collins, CO 80523-1874 The North Haugh [email protected] St Andrews, Fife KY16 9SS, U.K. [email protected] ABSTRACT permutation is thus the identity element ( ).) In the sym- We show how to compute efficiently a lexicographic order- metric group Sn this comparison of elements takes at most ing for subgroups and cosets of permutation groups and, n point comparisons. In a similar way a total order on a field F induces a to- more generally, of finite groups with a faithful permutation n representation. tal lexicographic order on the n-dimensional row space F which in turn induces a total (again lexicographic) order on the set F n×n of n×n matrices with entries in F . A compar- Categories and Subject Descriptors ison of two matrices takes at most n2 comparisons of field F[2]: 2; G [2]: 1; I [1]: 2 elements. As a third case we consider the automorphism group G of a (finite) group A. A total order on the elements of A again General Terms induces a total order on the elements of G by lexicographic Algorithms comparison of the images of a generating list L of A. (It can be convenient to take L to be sorted as well. The most Keywords “generic” choice is probably L = A.) Comparison of two automorphisms will take at most |L| comparisons of images.
    [Show full text]
  • Implementing Language-Dependent Lexicographic Orders in Scheme
    Implementing Language-Dependent Lexicographic Orders in Scheme Jean-Michel HUFFLEN LIFC (EA CNRS 4157) — University of Franche-Comté 16, route de Gray — 25030 BESANÇON CEDEX — FRANCE Abstract algorithm related to Unicode, an industry standard designed to al- The lexicographical order relations used within dictionaries are low text and symbols from all of the writing systems of the world to language-dependent, and we explain how we implemented such be consistently represented [2006]. Our method can be generalised orders in Scheme. We show how our sorting orders are derived to other alphabets. In addition, let us mention that if a document from the Unicode collation algorithm. Since the result of a Scheme cites some works written using the Latin alphabet and some writ- function can be itself a function, we use generators of sorting ten using another alphabet (Arabic, Cyrillic, . ), they are usually orders. Specifying a sorting order for a new natural language has itemised in two separate bibliography sections. So this limitation is been made as easy as possible and can be done by a programmer not too restrictive within MlBIBTEX’s purpose. who just has basic knowledge of Scheme. We also show how The next section of this article is devoted to some examples Scheme data structures allow our functions to be programmed in order to give some idea of this task’s complexity. We briefly efficiently. recall the principles of the Unicode collation algorithm [2006a] in Section 3 and explain how we adapted it in Scheme in Section 4. Keywords Lexicographical order relations, collation algorithm, Section 5 discusses some points, gives some limitations of our Unicode, MlBIBTEX, Scheme.
    [Show full text]
  • 1 Alphabets and Languages
    1 Alphabets and Languages Look at handout 1 (inference rules for sets) and use the rules on some exam- ples like fag ⊆ ffagg fag 2 fa; bg, fag 2 ffagg, fag ⊆ ffagg, fag ⊆ fa; bg, a ⊆ ffagg, a 2 fa; bg, a 2 ffagg, a ⊆ fa; bg Example: To show fag ⊆ fa; bg, use inference rule L1 (first one on the left). This asks us to show a 2 fa; bg. To show this, use rule L5, which succeeds. To show fag 2 fa; bg, which rule applies? • The only one is rule L4. So now we have to either show fag = a or fag = b. Neither one works. • To show fag = a we have to show fag ⊆ a and a ⊆ fag by rule L8. The only rules that might work to show a ⊆ fag are L1, L2, and L3 but none of them match, so we fail. • There is another rule for this at the very end, but it also fails. • To show fag = b, we try the rules in a similar way, but they also fail. Therefore we cannot show that fag 2 fa; bg. This suggests that the state- ment fag 2 fa; bg is false. Suppose we have two set expressions only involving brackets, commas, the empty set, and variables, like fa; fb; cgg and fa; fc; bgg. Then there is an easy way to test if they are equal. If they can be made the same by • permuting elements of a set, and • deleting duplicate items of a set then they are equal, otherwise they are not equal.
    [Show full text]
  • Context Free Languages II Announcement Announcement
    Announcement • About homework #4 Context Free Languages II – The FA corresponding to the RE given in class may indeed already be minimal. – Non-regular language proofs CFLs and Regular Languages • Use Pumping Lemma • Homework session after lecture Announcement Before we begin • Note about homework #2 • Questions from last time? – For a deterministic FA, there must be a transition for every character from every state. Languages CFLs and Regular Languages • Recall. • Venn diagram of languages – What is a language? Is there – What is a class of languages? something Regular Languages out here? CFLs Finite Languages 1 Context Free Languages Context Free Grammars • Context Free Languages(CFL) is the next • Let’s formalize this a bit: class of languages outside of Regular – A context free grammar (CFG) is a 4-tuple: (V, Languages: Σ, S, P) where – Means for defining: Context Free Grammar • V is a set of variables Σ – Machine for accepting: Pushdown Automata • is a set of terminals • V and Σ are disjoint (I.e. V ∩Σ= ∅) •S ∈V, is your start symbol Context Free Grammars Context Free Grammars • Let’s formalize this a bit: • Let’s formalize this a bit: – Production rules – Production rules →β •Of the form A where • We say that the grammar is context-free since this ∈ –A V substitution can take place regardless of where A is. – β∈(V ∪∑)* string with symbols from V and ∑ α⇒* γ γ α • We say that γ can be derived from α in one step: • We write if can be derived from in zero –A →βis a rule or more steps.
    [Show full text]