19770013605.Pdf
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Light Interaction with Matter Lesson Plan
Penn State RET in Interdisciplinary Materials Teacher’s Preparatory Guide : GILBERT AMADI Lab Title: Interaction of Light with Matter Purpose: In this unit, students are expected to learn: • How the light can be absorbed or scattered by small objects such as nanoparticles; • How light can be used to monitor the absorption and scattering of solutions; • How to compare light absorption, fluorescence, and light scattering; and • Color sensitivity of the absorption, scattering and fluorescence of a materials. Learning objectives: To recognize the experimental evidence for the wave nature of light. To understand that light travels with different speeds in different media To know the difference between turbidity and light absorbance To explore how different wavelengths interfere with different solution media To understand how blue, green and red) light from hand-hold laser pointers interact with different materials, including nanoparticles, fluorescence dye and milk. To understand the difference between absorbance and fluorescence Time required: 2-3 periods Level: High school National Science Education Standards : 11-12th grade Content Standard A • Abilities necessary to do scientific inquiry Content Standard B • Structure and properties of Light • Light Interaction with matter • Transfer of Energy • Light transmission, absorption, and scattering. • Energy as a property of many substances and its association with heat. • Light, electricity, mechanical motion, sound, atomic, nuclei, and the nature of a chemical • Energy transfer. This -

15.3 Heterogeneous Aqueous Systems 15.3
chem_TE_ch15_PPL.fm Page 459 Wednesday, August 4, 2004 5:53 AM 15.3 Heterogeneous Aqueous Systems 15.3 1 FOCUS Connecting to Your World It wiggles and jiggles. It comes Guide for Reading in many colors and flavors. When you pop it in your mouth, it dissolves. It Key Concepts Objectives is gelatin, one of the most popular desserts in the United States. In fact, • What is the difference between 15.3.1 Distinguish between a suspen- more than a million packages of gelatin are purchased a suspension and a solution? or eaten every day. Gelatin has even traveled into • What distinguishes a colloid sion and a solution. space. In 1996, American astronaut Shannon from a suspension and a 15.3.2 Identify the distinguishing solution? Lucid shared a gelatin dessert with her characteristic of a colloid. Russian crewmates. Gelatin is a heteroge- Vocabulary neous mixture called a colloid. In this section, suspension colloid Guide for Reading you will learn more about the characteristics Tyndall effect of colloids and a related mixture called a Brownian motion Build Vocabulary L2 suspension. emulsion Reading Strategy Venn Diagram Have students make a Previewing Before you read, Venn diagram using the following rewrite the headings of this sec- vocabulary terms: solution, suspension, tion as questions. As you read, colloid, Tyndall effect, Brownian motion. Suspensions write answers to your questions. So far in this chapter, you have learned about homogeneous mixtures that Reading Strategy L2 are formed when compounds such as inorganic acids, bases, and ionic salts Predict Before students begin to read mix with water. -

Research Papers-Mechanics / Electrodynamics/Download/305
WHY IS THE SKY BLUE? by Miles Mathis for the world is hollow and I have touched the sky Abstract: I will show that the current explanation is upside down. In researching this topic, I was surprised to find two different answers from two of the top mouthpieces of current physics. The top answer on a Yahoo search is by Philip Gibbs at the University of California, Riverside 1. It is that blue light is bent more than other colors. Gibbs shows us this illustration: Problem there is that we can move the Sun a few degrees and switch that effect. Just take the Sun above the first guy and he sees an unbent blue ray. The other guy sees a bent red ray. Light must be coming from all directions, not just the direction of the Sun, so this illustration is more than useless, it is misleading. Gibbs then shows it is air molecules, not dust, that do the bending, and he tells us that Einstein calculated in 1911 the scattering by molecules. These equations of Einstein are said to be “in agreement with experiment.” We are told, “the electromagnetic field of the light waves induces electric dipole moments in the molecules.” Gibbs then asks the million dollar question: “Why not violet?” If short wavelengths are bent more than long, then violet should be bent even more than blue, and the sky should be violet. He says it is due to the cones in our eyes. He shows the figure here and says that violet light stimulates red as well, making us see blue. -

Gold and Silver Nanoparticles
Gold and Silver Nanoparticles Copyright © 2012 Board of Trustees, University of Illinois. All rights reserved. Objectives You will: • Make gold nanoparticles • Make silver nanoparticles • Determine the color of the nanoparticles • Determine the size of the nanoparticles 2 How Big is a Nanometer? • 1 meter (m): Doorway ~2 meters high • 1 millimeter (mm): Thickness of a dime • 1 micrometer (mm): Size of a bacterium • 1 nanometer (nm): Diameter of DNA ~2 nm 3 Nanoparticles • Nanoparticles of a material behave differently than larger amounts of the same material. 4 What Color is Gold? • For instance, a nugget of gold large enough to hold has the same chemical and electrical properties as another nugget. • But two nanoparticles of pure gold exhibit markedly different physical properties - such as different colors – at differing distances between particles. 5 How Big are the Nanoparticles? • How big are the particles of gold and silver we will make? • We can get idea by looking at three properties. – Settling – Tyndall effect – Filtering 6 Settling • Settle out – See particles on bottom – Large particles (more than 1000 nm) • Remain dispersed – Never see particles on bottom – Smaller particles (less than 1000 nm) – May be clear or cloudy 7 Tyndall Effect • Tyndall effect is based on light scattering when it hits the particles in the mixture. – Tyndall effect – light scattered Tyndall Effect by particles • See line of light • Particles larger than 1 nm – No Tyndall effect – light passes without scattering • No line • Particles less than 1 nm No Tyndall Effect 8 Classifying Mixtures Tyndall Settling Size effect Solution Doesn’t No Light Less than 1 Settle Scattering nm Colloid Doesn’t Light 1 to 1000 Settle Scattering nm Suspension Settles Light More than Scattering 1000 nm 9 Solutions • Particles in a solution are so small that they do not settle; the movement of molecules is enough to keep them dispersed. -

Why the Sky Is Blue Puthalath Koroth Raghuprasada) 2400 E
PHYSICS ESSAYS 30, 1 (2017) Why the sky is blue Puthalath Koroth Raghuprasada) 2400 E. 8th Sreet, Odessa, Texas 79761, USA (Received 13 April 2013; accepted 14 February 2017; published online 3 March 2017) Abstract: The “Tyndall effect” and “Rayleigh scattering” are the accepted explanations for the blue color of the sky. However, since heavy rainfall is known to remove particulates as well as the gases and yet the sky actually becomes a deeper blue in color, both explanations are probably invalid. The current author proposes the following explanation for the blue color of the sky: This is the pale blue of ozone gas, which will appear deeper blue when there are sufficient quantities of it. Further, ozone attains an even deeper blue color when it becomes a liquid at around a temperature of 161 K (-112 C) and a blue to violet-black solid at temperatures below 82 K (-193.2 C). The lat- ter is the case in the lower Stratosphere, especially near the poles. Also, since ozone absorbs ultra- violet radiations, it is likely that some of the spectra close to UV (such as violet, indigo, and blue) radiations are also absorbed or scattered by ozone and this may add to the blue color of the ozone layer. To an observer on the surface of the earth, the many layers of dust and other particulates in the intervening Troposphere, which dampen the deep blue of the ozone layer, will make the “sky” appear less blue. How much each of the above factors contributes to the color of the sky is not known but jointly, they can explain all the observed phenomena. -

7A.F.G.F. Colloids.Emuls.Pdf
Colloids 1.1. TerminologyTerminology ,, definitions,definitions, clasificationclasification Colloid systems (or simply colloids) – dispersions systems, mostly bi-components, looking as physically uniform, but if fact they are not molecularly dispersed. Thus, although colloid is a substance microscopically dispersed evenly throughout another one, it consists of two separate phases : a dispersed phase (or internal phase) and a continuous phase (or dispersion medium, solvent). The size of dispersed phase is between 1nm – 1000 nm (1µm). They are in the range between molecular size (that in solutions) and mechanical dispersions (suspensions). They can be mono-dispersed or poly-dispersed. Colloidal systems may be solid, liquid, or gaseous. They can be classified as shown in Table 1. Colloids Table 1 . Classification of colloid systems Continuous Internal Name Examples phase phase Gas Does not exist, all gases are mutually miscible Gas Liquid aerosol fog, mist, hair sprays Solid solid aerosol smoke, cloud, air particulates Gas foams, sols whipped cream, shaving cream, detergent Liquid foam Liquid lyosols, emulsoids milk, mayonnaise, hand cream, gelatins, proteins Solid lyosols, pigmented ink, blood, metal sols, sulfides, suspensoids Me(OH) y, Me xOy Gas solid foams aerogels, styrofoams, pumice, gas occlusions Solid in minerals Liquid solid foams, gels agar, gelatin, jelly, silicagel, opal Solid solid sols cranberry glasses, microcosmic salt bead, NaCl crystals impured with colloidal metallic Na particles. 2. Occurrence of colloid systems Colloids -

Web Pages-Optical Properties
Material Science Prof. Satish V. Kailas Associate Professor Dept. of Mechanical Engineering, Indian Institute of Science, Bangalore – 560012 India Chapter 17. Optical properties • Optical property of a material is defined as its interaction with electro-magnetic radiation in the visible. • Electromagnetic spectrum of radiation spans the wide range from γ-rays with wavelength as 10-12 m, through x-rays, ultraviolet, visible, infrared, and finally radio waves with wavelengths as along as 105 m. • Visible light is one form of electromagnetic radiation with wavelengths ranging from 0.39 to 0.77 μm. • Light can be considered as having waves and consisting of particles called photons. hc • Energy E of a photon hE ν == 0 λ o h – Planck’s constant (6.62x10-34 J.sec), o ν – frequency, 8 o c0 – speed of light in vacuum (3x10 m/sec), and o λ – wavelength. Electro-magnetic radiation Material – Light interaction • Interaction of photons with the electronic or crystal structure of a material leads to a number of phenomena. • The photons may give their energy to the material (absorption); photons give their energy, but photons of identical energy are immediately emitted by the material (reflection); photons may not interact with the material structure (transmission); or during transmission photons are changes in velocity (refraction). • At any instance of light interaction with a material, the total intensity of the incident light striking a surface is equal to sum of the absorbed, reflected, and transmitted intensities. 0 = + + IIII TRA • Where the intensity ‘I ‘is defined as the number of photons impinging on a surface per unit area per unit time. -

Subject: Chemistry Date -11/08/2021 1.What Is a Suspension?
Class: IX Topic: Is matter around us pure? Subject: Chemistry Date -11/08/2021 1.What is a suspension? A suspension is formed when two or more substances are mixed in a non-uniform manner. Heterogeneous mixtures are suspensions. The solute does not mix with the solvent and can be viewed through naked eyes. Properties of Suspensions: • A suspension is a heterogeneous mixture. • We can see the particles of suspensions through naked eyes. • We can see the path of light through the particles of a suspension..This is called Tyndall effect. • The particles of suspension tend to settle down when left undisturbed. Then, they can be separated using filtration. • The size of the particles of solute is more than 1000nm. • The suspension is unstable in nature. 2.What are colloids or colloidal solutions? A colloidal solution or a colloid is a uniform solution of two or more substances. The particles are relatively smaller than suspension .It appears as a homogeneous mixture but it is not. Properties of colloids: • Colloids are heterogeneous in nature. • The particles of a colloid cannot be seen through naked eyes. • The particles scatter a beam of light passed through a colloid and produce Tyndall effect. • Colloids are stable in nature. The particles of colloids do not settle down if left uninterrupted. • We cannot separate the particles of a colloid through filtration. We use a method called Centrifugation to separate the particles of a colloid. • The size of particles of colloid is 1to 1000 nm. 3.What is the Tyndall Effect? When a beam of light is passed through a colloid the particles of the colloid scatter the beam of light and we can see the path of light in the solution. -

Size Determination Via Dynamic Light Scattering
Size determination via dynamic light scattering Theory: Light scattering Colloidal particles when immersed in a fluid are able to scatter a beam of light (the Tyndall effect). The scattering pattern (i.e. the intensity of the scattered light as a function of θ, the angle between the incident beam and the scattered beam) depends very strongly on the particle size and on the wavelength of the light. The spectral colours that are sometimes generated have fascinated investigators since before the end of the nineteenth century. It is only very recently, that the full potentialities of the study of light scattering have been realized, with the introduction of lasers to give coherent, monochromatic, intense and narrow incident beams, together with sensitive and stable photon-detection apparatus and rapid data analysis by computer. Dynamic light scattering This procedure depends on the fact that, if the scattering particle is moving when the light photon hits it then the re-radiated light will have a slightly different frequency when viewed by a stationary observer. This is why it is called quasi-elastic or dynamic light scattering . The frequency is slightly increased or decreased depending on whether the particle is moving towards or away from the observer. This is called Doppler broadening and if it can be measured accurately it provides a means of determining the diffusion coefficient of the particle. The ZetaSizer can measure the size of particles with diameters from 3 to 1000 nm, using the method of photon correlation spectroscopy (PCS) or quasi-elastic light scattering (QELS) . Particles in this size range are called colloids. -
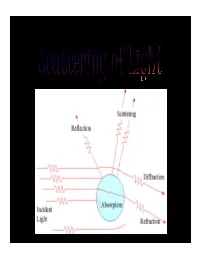
Scatteing of Light.Pdf
INTRODUCTION • Definition:- “ Light scattering is a form of scattering in which light is the form of propagating energy which is scattered. Light scattering can be thought of as the deflection of a ray from a straight path, for example by irregularities in the propagation medium, particles, or in the interface between two media.” “Scattering is a general physical process whereby some forms of radiation, such as light or moving particles, for example, are forced to deviate from a straight trajectory by one or more localized non-uniformities in the medium through which it passes.” • Most objects that one sees are visible due to light scattering from their surfaces. Indeed, this is our primary mechanism of physical observation. • Scattering of light depends on the wavelength or frequency of the light being scattered. Since visible light has wavelength on the order of a micrometre, objects much smaller than this cannot be seen, even with the aid of a microscope. • Colloidal particles as small as 1 µm have been observed directly in aqueous suspension. IMPORTANCE OF SCATTERING OF LIGHT • The interaction of light with matter give important information about the structure and dynamics of the material being examined. • If the scattering centres are in motion, then the scattered radiation is Doppler shifted. An analysis of the spectrum of scattered light can thus yield information regarding the motion of the scattering center. Periodicity or structural repetition in the scattering medium will cause interference in the spectrum of scattered light. • Thus, a study of the scattered light intensity as a function of scattering angle gives information about the structure, spatial configuration, or morphology of the scattering medium. -
Class : X Topic: SCATTERING of LIGHT,TYNDALL EFFECT, NATURAL Subject: PHYSICS PHENOMENON
CLASS NOTES Class : X Topic: SCATTERING OF LIGHT,TYNDALL EFFECT, NATURAL Subject: PHYSICS PHENOMENON Correction- In the previous uploaded content of physics, make a correction in page1 DISPERSION OF WHITE LIGHT BY GLASS PRISM TheThe phenomenon phenomenon of of splitting splitting of of white white light light into into its its seven seven constituent constituent colours colors when it passes throughthrough a a glass glass prism prism is is called called dispersion dispersion of of white white light. light. The The various various colours colors seen are Violet, Indigo,Indigo, Blue, Blue, Green, Green, Yellow, Yellow, Orange Orange and and Red. Red. The The sequence sequence of of colours colors remembers as VIBGYOR. TheVIBGYOR. band of The seven band colours of seven is called colors the is calledspectrum. the spectrum.The different The component different component colour of light colour bends atof a lightdifferent bends angle at a withdifferent respect angle to withthe incident respect angle.to the Theincide violetnt angle. light bendsThe violet the lightmost bends while the Red bends the least. the MOST while the Red bends the LEAST SCATTERING OF LIGHT Scattering of light is the phenomenon in which light rays get deviated from its straight path on striking an obstacle like dust or gas molecules, water vapours etc. Scattering of light gives rise to many spectacular phenomena such as Tyndall effect and the “red hues of sunrise and sunset”. The colors we see in the sky are due to scattering of light. Tyndall Effect Tyndall effect is the phenomenon of scattering of light by colloidal particles. -

Solutions and Colloids
SOLUTIONS AND COLLOIDS OBJECTIVES 1. To examine the influence of solvent and solute on solution formation 2. To prepare a solution for use in a later experiment 3. To make a colloid and demonstrate its properties INTRODUCTION Part I. Influence of solute and solvent on solubility Solutions are homogeneous mixtures of two or more chemical substances. The components can be gases, liquids, or solids, and they are uniformly distributed. As a result, the properties of a true solution are the same throughout the solution. The component of a solution that produces dissolution is called the solvent and is often present in greater proportion. The component that is dissolved is called the solute. The components of the solution are of atomic or molecular size. Thus they are too small to reflect light and solutions will be transparent, though they may be colored or colorless. Often, then, it becomes necessary to use chemical and physical tests to identify a substance as a solution rather than as pure solvent. Chemical tests, such as the formation of a precipitate (studied in the experiment on chemical reactions), are frequently used to identify ions or molecules in a solution. The solubility of a solute in a particular solvent is a property of that solute. Commonly, the solubility of a solute in a liquid is reported in grams of solute per 100 mL of solvent. Several factors may influence the solubility of a solute, including temperature, the nature of the solute, and the nature of the solvent. To understand how the nature of the solute and solvent affect solubility, the concept of intermolecular forces must be examined.