Applications of Single-Photon Two-Qubit Quantum Logic to the Quantum Information Science Taehyun
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

On the Lattice Structure of Quantum Logic
BULL. AUSTRAL. MATH. SOC. MOS 8106, *8IOI, 0242 VOL. I (1969), 333-340 On the lattice structure of quantum logic P. D. Finch A weak logical structure is defined as a set of boolean propositional logics in which one can define common operations of negation and implication. The set union of the boolean components of a weak logical structure is a logic of propositions which is an orthocomplemented poset, where orthocomplementation is interpreted as negation and the partial order as implication. It is shown that if one can define on this logic an operation of logical conjunction which has certain plausible properties, then the logic has the structure of an orthomodular lattice. Conversely, if the logic is an orthomodular lattice then the conjunction operation may be defined on it. 1. Introduction The axiomatic development of non-relativistic quantum mechanics leads to a quantum logic which has the structure of an orthomodular poset. Such a structure can be derived from physical considerations in a number of ways, for example, as in Gunson [7], Mackey [77], Piron [72], Varadarajan [73] and Zierler [74]. Mackey [77] has given heuristic arguments indicating that this quantum logic is, in fact, not just a poset but a lattice and that, in particular, it is isomorphic to the lattice of closed subspaces of a separable infinite dimensional Hilbert space. If one assumes that the quantum logic does have the structure of a lattice, and not just that of a poset, it is not difficult to ascertain what sort of further assumptions lead to a "coordinatisation" of the logic as the lattice of closed subspaces of Hilbert space, details will be found in Jauch [8], Piron [72], Varadarajan [73] and Zierler [74], Received 13 May 1969. -

Relational Quantum Mechanics
Relational Quantum Mechanics Matteo Smerlak† September 17, 2006 †Ecole normale sup´erieure de Lyon, F-69364 Lyon, EU E-mail: [email protected] Abstract In this internship report, we present Carlo Rovelli’s relational interpretation of quantum mechanics, focusing on its historical and conceptual roots. A critical analysis of the Einstein-Podolsky-Rosen argument is then put forward, which suggests that the phenomenon of ‘quantum non-locality’ is an artifact of the orthodox interpretation, and not a physical effect. A speculative discussion of the potential import of the relational view for quantum-logic is finally proposed. Figure 0.1: Composition X, W. Kandinski (1939) 1 Acknowledgements Beyond its strictly scientific value, this Master 1 internship has been rich of encounters. Let me express hereupon my gratitude to the great people I have met. First, and foremost, I want to thank Carlo Rovelli1 for his warm welcome in Marseille, and for the unexpected trust he showed me during these six months. Thanks to his rare openness, I have had the opportunity to humbly but truly take part in active research and, what is more, to glimpse the vivid landscape of scientific creativity. One more thing: I have an immense respect for Carlo’s plainness, unaltered in spite of his renown achievements in physics. I am very grateful to Antony Valentini2, who invited me, together with Frank Hellmann, to the Perimeter Institute for Theoretical Physics, in Canada. We spent there an incredible week, meeting world-class physicists such as Lee Smolin, Jeffrey Bub or John Baez, and enthusiastic postdocs such as Etera Livine or Simone Speziale. -

Why Feynman Path Integration?
Journal of Uncertain Systems Vol.5, No.x, pp.xx-xx, 2011 Online at: www.jus.org.uk Why Feynman Path Integration? Jaime Nava1;∗, Juan Ferret2, Vladik Kreinovich1, Gloria Berumen1, Sandra Griffin1, and Edgar Padilla1 1Department of Computer Science, University of Texas at El Paso, El Paso, TX 79968, USA 2Department of Philosophy, University of Texas at El Paso, El Paso, TX 79968, USA Received 19 December 2009; Revised 23 February 2010 Abstract To describe physics properly, we need to take into account quantum effects. Thus, for every non- quantum physical theory, we must come up with an appropriate quantum theory. A traditional approach is to replace all the scalars in the classical description of this theory by the corresponding operators. The problem with the above approach is that due to non-commutativity of the quantum operators, two math- ematically equivalent formulations of the classical theory can lead to different (non-equivalent) quantum theories. An alternative quantization approach that directly transforms the non-quantum action functional into the appropriate quantum theory, was indeed proposed by the Nobelist Richard Feynman, under the name of path integration. Feynman path integration is not just a foundational idea, it is actually an efficient computing tool (Feynman diagrams). From the pragmatic viewpoint, Feynman path integral is a great success. However, from the founda- tional viewpoint, we still face an important question: why the Feynman's path integration formula? In this paper, we provide a natural explanation for Feynman's path integration formula. ⃝c 2010 World Academic Press, UK. All rights reserved. Keywords: Feynman path integration, independence, foundations of quantum physics 1 Why Feynman Path Integration: Formulation of the Problem Need for quantization. -
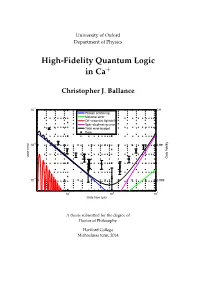
High-Fidelity Quantum Logic in Ca+
University of Oxford Department of Physics High-Fidelity Quantum Logic in Ca+ Christopher J. Ballance −1 10 0.9 Photon scattering Motional error Off−resonant lightshift Spin−dephasing error Total error budget Data −2 10 0.99 Gate error Gate fidelity −3 10 0.999 1 2 3 10 10 10 Gate time (µs) A thesis submitted for the degree of Doctor of Philosophy Hertford College Michaelmas term, 2014 Abstract High-Fidelity Quantum Logic in Ca+ Christopher J. Ballance A thesis submitted for the degree of Doctor of Philosophy Michaelmas term 2014 Hertford College, Oxford Trapped atomic ions are one of the most promising systems for building a quantum computer – all of the fundamental operations needed to build a quan- tum computer have been demonstrated in such systems. The challenge now is to understand and reduce the operation errors to below the ‘fault-tolerant thresh- old’ (the level below which quantum error correction works), and to scale up the current few-qubit experiments to many qubits. This thesis describes experimen- tal work concentrated primarily on the first of these challenges. We demonstrate high-fidelity single-qubit and two-qubit (entangling) gates with errors at or be- low the fault-tolerant threshold. We also implement an entangling gate between two different species of ions, a tool which may be useful for certain scalable architectures. We study the speed/fidelity trade-off for a two-qubit phase gate implemented in 43Ca+ hyperfine trapped-ion qubits. We develop an error model which de- scribes the fundamental and technical imperfections / limitations that contribute to the measured gate error. -

Analysis of Nonlinear Dynamics in a Classical Transmon Circuit
Analysis of Nonlinear Dynamics in a Classical Transmon Circuit Sasu Tuohino B. Sc. Thesis Department of Physical Sciences Theoretical Physics University of Oulu 2017 Contents 1 Introduction2 2 Classical network theory4 2.1 From electromagnetic fields to circuit elements.........4 2.2 Generalized flux and charge....................6 2.3 Node variables as degrees of freedom...............7 3 Hamiltonians for electric circuits8 3.1 LC Circuit and DC voltage source................8 3.2 Cooper-Pair Box.......................... 10 3.2.1 Josephson junction.................... 10 3.2.2 Dynamics of the Cooper-pair box............. 11 3.3 Transmon qubit.......................... 12 3.3.1 Cavity resonator...................... 12 3.3.2 Shunt capacitance CB .................. 12 3.3.3 Transmon Lagrangian................... 13 3.3.4 Matrix notation in the Legendre transformation..... 14 3.3.5 Hamiltonian of transmon................. 15 4 Classical dynamics of transmon qubit 16 4.1 Equations of motion for transmon................ 16 4.1.1 Relations with voltages.................. 17 4.1.2 Shunt resistances..................... 17 4.1.3 Linearized Josephson inductance............. 18 4.1.4 Relation with currents................... 18 4.2 Control and read-out signals................... 18 4.2.1 Transmission line model.................. 18 4.2.2 Equations of motion for coupled transmission line.... 20 4.3 Quantum notation......................... 22 5 Numerical solutions for equations of motion 23 5.1 Design parameters of the transmon................ 23 5.2 Resonance shift at nonlinear regime............... 24 6 Conclusions 27 1 Abstract The focus of this thesis is on classical dynamics of a transmon qubit. First we introduce the basic concepts of the classical circuit analysis and use this knowledge to derive the Lagrangians and Hamiltonians of an LC circuit, a Cooper-pair box, and ultimately we derive Hamiltonian for a transmon qubit. -

Theoretical Physics Group Decoherent Histories Approach: a Quantum Description of Closed Systems
Theoretical Physics Group Department of Physics Decoherent Histories Approach: A Quantum Description of Closed Systems Author: Supervisor: Pak To Cheung Prof. Jonathan J. Halliwell CID: 01830314 A thesis submitted for the degree of MSc Quantum Fields and Fundamental Forces Contents 1 Introduction2 2 Mathematical Formalism9 2.1 General Idea...................................9 2.2 Operator Formulation............................. 10 2.3 Path Integral Formulation........................... 18 3 Interpretation 20 3.1 Decoherent Family............................... 20 3.1a. Logical Conclusions........................... 20 3.1b. Probabilities of Histories........................ 21 3.1c. Causality Paradox........................... 22 3.1d. Approximate Decoherence....................... 24 3.2 Incompatible Sets................................ 25 3.2a. Contradictory Conclusions....................... 25 3.2b. Logic................................... 28 3.2c. Single-Family Rule........................... 30 3.3 Quasiclassical Domains............................. 32 3.4 Many History Interpretation.......................... 34 3.5 Unknown Set Interpretation.......................... 36 4 Applications 36 4.1 EPR Paradox.................................. 36 4.2 Hydrodynamic Variables............................ 41 4.3 Arrival Time Problem............................. 43 4.4 Quantum Fields and Quantum Cosmology.................. 45 5 Summary 48 6 References 51 Appendices 56 A Boolean Algebra 56 B Derivation of Path Integral Method From Operator -

Are Non-Boolean Event Structures the Precedence Or Consequence of Quantum Probability?
Are Non-Boolean Event Structures the Precedence or Consequence of Quantum Probability? Christopher A. Fuchs1 and Blake C. Stacey1 1Physics Department, University of Massachusetts Boston (Dated: December 24, 2019) In the last five years of his life Itamar Pitowsky developed the idea that the formal structure of quantum theory should be thought of as a Bayesian probability theory adapted to the empirical situation that Nature’s events just so happen to conform to a non-Boolean algebra. QBism too takes a Bayesian stance on the probabilities of quantum theory, but its probabilities are the personal degrees of belief a sufficiently- schooled agent holds for the consequences of her actions on the external world. Thus QBism has two levels of the personal where the Pitowskyan view has one. The differences go further. Most important for the technical side of both views is the quantum mechanical Born Rule, but in the Pitowskyan development it is a theorem, not a postulate, arising in the way of Gleason from the primary empirical assumption of a non-Boolean algebra. QBism on the other hand strives to develop a way to think of the Born Rule in a pre-algebraic setting, so that it itself may be taken as the primary empirical statement of the theory. In other words, the hope in QBism is that, suitably understood, the Born Rule is quantum theory’s most fundamental postulate, with the Hilbert space formalism (along with its perceived connection to a non-Boolean event structure) arising only secondarily. This paper will avail of Pitowsky’s program, along with its extensions in the work of Jeffrey Bub and William Demopoulos, to better explicate QBism’s aims and goals. -

Quantum Simulation of the Single-Particle Schrodinger Equation
Quantum simulation of the single-particle Schr¨odinger equation 1,2, 3, Giuliano Benenti ∗ and Giuliano Strini † 1CNISM, CNR-INFM & Center for Nonlinear and Complex Systems, Universit`adegli Studi dell’Insubria, Via Valleggio 11, 22100 Como, Italy 2Istituto Nazionale di Fisica Nucleare, Sezione di Milano, via Celoria 16, 20133 Milano, Italy 3Dipartimento di Fisica, Universit`adegli Studi di Milano, Via Celoria 16, 20133 Milano, Italy (Dated: May 21, 2018) The working of a quantum computer is described in the concrete example of a quantum simulator of the single-particle Schr¨odinger equation. We show that a register of 6 − 10 qubits is sufficient to realize a useful quantum simulator capable of solving in an efficient way standard quantum mechanical problems. I. INTRODUCTION II. QUANTUM LOGIC 1,2 The elementary unit of quantum information is the During the last years quantum information has be- qubit (the quantum counterpart of the classical bit) and come one of the new hot topic field in physics, with the a quantum computer may be viewed as a many-qubit potential to revolutionize many areas of science and tech- system. Physically, a qubit is a two-level system, like nology. Quantum information replaces the laws of classi- 1 the two spin states of a spin- 2 particle, the polarization cal physics, applied to computation and communication, states of a single photon or two states of an atom. with the more fundamental laws of quantum mechanics. A classical bit is a system that can exist in two dis- This becomes increasingly important due to technological tinct states, which are used to represent 0 and 1, that progress reaching smaller and smaller scales. -

Peter Mittelstaedt's Contributions to Physics and Its Foundations
This is a repository copy of Quantum-Matter-Spacetime : Peter Mittelstaedt's Contributions to Physics and Its Foundations. White Rose Research Online URL for this paper: https://eprints.whiterose.ac.uk/42664/ Version: Submitted Version Article: Busch, P. orcid.org/0000-0002-2559-9721, Pfarr, J., Ristig, M.L. et al. (1 more author) (2010) Quantum-Matter-Spacetime : Peter Mittelstaedt's Contributions to Physics and Its Foundations. Foundations of Physics. pp. 1163-1170. ISSN 0015-9018 https://doi.org/10.1007/s10701-010-9478-3 Reuse Items deposited in White Rose Research Online are protected by copyright, with all rights reserved unless indicated otherwise. They may be downloaded and/or printed for private study, or other acts as permitted by national copyright laws. The publisher or other rights holders may allow further reproduction and re-use of the full text version. This is indicated by the licence information on the White Rose Research Online record for the item. Takedown If you consider content in White Rose Research Online to be in breach of UK law, please notify us by emailing [email protected] including the URL of the record and the reason for the withdrawal request. [email protected] https://eprints.whiterose.ac.uk/ promoting access to White Rose research papers Universities of Leeds, Sheffield and York http://eprints.whiterose.ac.uk/ This is an author produced version of a paper published in FOUNDATIONS OF PHYSICS White Rose Research Online URL for this paper: http://eprints.whiterose.ac.uk/42664 Published paper Title: Quantum-Matter-Spacetime: Peter Mittelstaedt's Contributions to Physics and Its Foundations Author(s): Busch, P; Pfarr, J; Ristig, ML, et al. -

QUANTUM. LOGIC Gjj
QUANTUM. LOGIC gJJ DAVID J. FpCLlS , Ulliversily o{ Massa ι'hmells , Alldlt!rSI. ,Hassacllllsl'llS, L:.5..-\. (5ecs. 1-3) Rr CHARD J. GREECHIE, Louisial1 a Tech Ulli\'ersil γ , RU5(Oll, Louisialla, U. 5.A. (5 1' ι'5. 1-3) MARIA LOUISA DALLA CHIA民主 AND ROBERTO GIUNTINI, Ullivt!rsità di Firω, 1: 1', Flore l1 ce, llalv (5ecs. 4一 10) Introduction ...... ................. 229 3.4 Cartesian and T ensor Products 1. A Brief History of Quantum of Orthoalgebras .................. 238 Logic .................................. 230 3.5 The Logic of a Physical - 'EA - The Origin of Quantum Svstem ................................ 239 Logic .................................. 230 3.6 The Canonical Mapping ........ 240 1.2 The Work of Birkhoff and von 3.7 Critique of Quantum Logic ... 240 Neumann ...……-………..….. 230 4. The Logician's Approach .... 241 1.3 The Orthomodular Law ........ 231 S. Algebraic and Possible- 1.4 The Interpretation of Meet World Semantics ................ 242 and Join ..................... ......... 232 6. Orthodox Quantum Logic ... 243 2. Standard Quantum Logic .... 232 6.1 Semamic Characterizations of 2.1 The Orthomodular Lattice of QL ...................................... 243 Projections on a Hilbert An Axiomatization of QL ...... 244 Space .................................. 232 6.2 2.2 Observables ......................... 233 7. Orthologic and Unsharp 2.3 States ...........…..………........ 234 Quantum Logics ................. 245 2.4 Superposition of States ......... 235 8. Hilbert-Space Models of the 2.5 Dynamics ............................ 235 Brouwer-Zadeh Logics ....... 247 2.6 Combinations of Standard 9. Partial Quantum Logics ...... 248 Quantum Logics ...... ............ 236 9.1 Algebraic Semantics for 3. Orthoalgebras 臼 Models for WPaQL ............................... 249 a General Quantum Logic '" 236 9.2 An Axiomatization of Partial 3.1 Orthoalgebras ...................... 236 Quantum Logics ................. -

Review of Jean Bricmont's Book" Making Sense of Quantum
Book Review of Jean Bricmont’s “Making Sense of Quantum Mechanics” Springer, 2016 Michael K.-H. Kiessling Department of Mathematics Rutgers, The State University of New Jersey 110 Frelinghuysen Rd., Piscataway, NJ 08854 c 2017 The author. Reproduction of this review, for noncommercial purposes only, is permitted. “Given that quantum mechanics was discovered ninety years ago, the present rather low level of understanding of its deeper meaning may be seen to represent some kind of intellectual scandal.” [BFS] Folklore has it that physicists, when they get “too old” for doing “real physics,” turn into “hobby philosophers” pondering the elusive “deeper meaning” of quantum mechanics, very much to the bemusement of their more practically minded younger peers. Closer to the truth than such feel-good folklore is the realization that physicists who try to understand what our practically successful most fundamental theories1 say about our world are also well aware of the professional mine field on which they are traipsing. Thus, with some notable exceptions, they simply don’t dare to risk ruining their scientific reputation with an offering of their secret thoughts on the subject before reaching retirement age. Even then, with ones career no longer in danger, such a step requires courage — after all, who enjoys the thought of “gos- sip among physicists brand[ing one] ‘senile’.”2 But for Jean Bricmont, well-known 1Beside quantum mechanics, I put general relativity theory in this category. 2I have adapted this quote from p.281 of the book, where Bricmont quotes John Clauser (his ref.[97]) saying furthermore: “I was personally told as student that these men [Einstein, Schr¨odinger, arXiv:1709.05442v1 [physics.hist-ph] 16 Sep 2017 de Broglie] had become senile, and that clearly their opinions could no longer be trusted in this regard. -

Path Integral Monte Carlo Simulations of Semiconductor Quantum Dots and Quantum Wires by Lei Zhang
Path Integral Monte Carlo Simulations of Semiconductor Quantum Dots and Quantum Wires by Lei Zhang A Dissertation Presented in Partial Fulfillment of the Requirements for the Degree Doctor of Philosophy Approved November 2011 by the Graduate Supervisory Committee: John Shumway, Chair Peter Bennet Kevin Schmidt Jose´ Menendez´ Jeff Drucker ARIZONA STATE UNIVERSITY December 2011 ABSTRACT The accurate simulation of many-body quantum systems is a chal- lenge for computational physics. Quantum Monte Carlo methods are a class of algorithms that can be used to solve the many-body problem. I study many-body quantum systems with Path Integral Monte Carlo techniques in three related areas of semiconductor physics: (1) the role of correlation in exchange coupling of spins in double quantum dots, (2) the degree of correlation and hyperpolarizability in Stark shifts in In- GaAs/GaAs dots, and (3) van der Waals interactions between 1-D metal- lic quantum wires at finite temperature. The two-site model is one of the simplest quantum problems, yet the quantitative mapping from a three-dimensional model of a quantum double dot to an effective two-site model has many subtleties requiring careful treatment of exchange and correlation. I calculate exchange cou- pling of a pair of spins in a double dot from the permutations in a bosonic path integral, using Monte Carlo method. I also map this problem to a Hubbard model and find that exchange and correlation renormalizes the model parameters, dramatically decreasing the effective on-site re- pulsion at larger separations. Next, I investigated the energy, dipole moment, polarizability and hyperpolarizability of excitonic system in InGaAs/GaAs quantum dots of different shapes and successfully give the photoluminescence spectra for different dots with electric fields in both the growth and transverse direction.