An Assessment of New Zealand's Height Systems and Options for A
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

The Ausgeoid09 Model of the Australian Height Datum
J Geod (2011) 85:133–150 DOI 10.1007/s00190-010-0422-2 ORIGINAL ARTICLE The AUSGeoid09 model of the Australian Height Datum W. E. Featherstone · J. F. Kirby · C. Hirt · M. S. Filmer · S. J. Claessens · N. J. Brown · G. Hu · G. M. Johnston Received: 7 June 2010 / Accepted: 15 October 2010 / Published online: 19 November 2010 © The Author(s) 2010. This article is published with open access at Springerlink.com Abstract AUSGeoid09 is the new Australia-wide gravi- Australia, it is necessary to provide GNSS users with metric quasigeoid model that has been a posteriori fitted effective means of recovering AHD heights. The gravi- to the Australian Height Datum (AHD) so as to provide a metric component of the quasigeoid model was computed product that is practically useful for the more direct deter- using a hybrid of the remove-compute-restore technique mination of AHD heights from Global Navigation Satel- with a degree-40 deterministically modified kernel over a lite Systems (GNSS). This approach is necessary because one-degree spherical cap, which is superior to the remove- the AHD is predominantly a third-order vertical datum that compute-restore technique alone in Australia (with or without contains a ∼1 m north-south tilt and ∼0.5 m regional distor- a cap). This is because the modified kernel and cap com- tions with respect to the quasigeoid, meaning that GNSS- bine to filter long-wavelength errors from the terrestrial gravimetric-quasigeoid and AHD heights are inconsistent. gravity anomalies. The zero-tide EGM2008 global gravi- Because the AHD remains the official vertical datum in tational model to degree 2,190 was used as the reference field. -

Meyers Height 1
University of Connecticut DigitalCommons@UConn Peer-reviewed Articles 12-1-2004 What Does Height Really Mean? Part I: Introduction Thomas H. Meyer University of Connecticut, [email protected] Daniel R. Roman National Geodetic Survey David B. Zilkoski National Geodetic Survey Follow this and additional works at: http://digitalcommons.uconn.edu/thmeyer_articles Recommended Citation Meyer, Thomas H.; Roman, Daniel R.; and Zilkoski, David B., "What Does Height Really Mean? Part I: Introduction" (2004). Peer- reviewed Articles. Paper 2. http://digitalcommons.uconn.edu/thmeyer_articles/2 This Article is brought to you for free and open access by DigitalCommons@UConn. It has been accepted for inclusion in Peer-reviewed Articles by an authorized administrator of DigitalCommons@UConn. For more information, please contact [email protected]. Land Information Science What does height really mean? Part I: Introduction Thomas H. Meyer, Daniel R. Roman, David B. Zilkoski ABSTRACT: This is the first paper in a four-part series considering the fundamental question, “what does the word height really mean?” National Geodetic Survey (NGS) is embarking on a height mod- ernization program in which, in the future, it will not be necessary for NGS to create new or maintain old orthometric height benchmarks. In their stead, NGS will publish measured ellipsoid heights and computed Helmert orthometric heights for survey markers. Consequently, practicing surveyors will soon be confronted with coping with these changes and the differences between these types of height. Indeed, although “height’” is a commonly used word, an exact definition of it can be difficult to find. These articles will explore the various meanings of height as used in surveying and geodesy and pres- ent a precise definition that is based on the physics of gravitational potential, along with current best practices for using survey-grade GPS equipment for height measurement. -

Literacy and Numeracy in Northern Ireland and the Republic of Ireland in International Studies
The Irish Journal of Education, 2015, xl, pp. 3-28. LITERACY AND NUMERACY IN NORTHERN IRELAND AND THE REPUBLIC OF IRELAND IN INTERNATIONAL STUDIES Gerry Shiel and Lorraine Gilleece Educational Research Centre St Patrick’s College, Dublin Recent international assessments of educational achievement at primary, post- primary, and adult levels allow for comparisons of performance in reading literacy and numeracy/mathematics between Northern Ireland and the Republic of Ireland. While students in grade 4 (Year 6) in Northern Ireland significantly outperformed students in the Republic in reading literacy and mathematics in the PIRLS and TIMSS studies in 2011, 15-year olds in the Republic outperformed students in Northern Ireland on reading and mathematical literacy in PISA 2006 and 2012. Performance on PISA reading literacy and mathematics declined significantly from performance in earlier cycles in Northern Ireland in 2006 and in the Republic of Ireland in 2009. However, while performance in the Republic improved in 2012, it has remained at about the same level since 2006 in Northern Ireland. Adults in both Northern Ireland and the Republic performed significantly below the international averages on literacy and numeracy in the 2012 PIAAC study. Results of the studies are discussed in the context of policy initiatives in 2011 to improve literacy and numeracy in both jurisdictions, including the implementation of literacy and numeracy strategies and the establishment of targets for improved performance at system and school levels. Both Northern -

What Are Geodetic Survey Markers?
Part I Introduction to Geodetic Survey Markers, and the NGS / USPS Recovery Program Stf/C Greg Shay, JN-ACN United States Power Squadrons / America’s Boating Club Sponsor: USPS Cooperative Charting Committee Revision 5 - 2020 Part I - Topics Outline 1. USPS Geodetic Marker Program 2. What are Geodetic Markers 3. Marker Recovery & Reporting Steps 4. Coast Survey, NGS, and NOAA 5. Geodetic Datums & Control Types 6. How did Markers get Placed 7. Surveying Methods Used 8. The National Spatial Reference System 9. CORS Modernization Program Do you enjoy - Finding lost treasure? - the excitement of the hunt? - performing a valuable public service? - participating in friendly competition? - or just doing a really fun off-water activity? If yes , then participation in the USPS Geodetic Marker Recovery Program may be just the thing for you! The USPS Triangle and Civic Service Activities USPS Cooperative Charting / Geodetic Programs The Cooperative Charting Program (Nautical) and the Geodetic Marker Recovery Program (Land Based) are administered by the USPS Cooperative Charting Committee. USPS Cooperative Charting / Geodetic Program An agreement first executed between USPS and NOAA in 1963 The USPS Geodetic Program is a separate program from Nautical and was/is not part of the former Cooperative Charting agreement with NOAA. What are Geodetic Survey Markers? Geodetic markers are highly accurate surveying reference points established on the surface of the earth by local, state, and national agencies – mainly by the National Geodetic Survey (NGS). NGS maintains a database of all markers meeting certain criteria. Common Synonyms Mark for “Survey Marker” Marker Marker Station Note: the words “Geodetic”, Benchmark* “Survey” or Station “Geodetic Survey” Station Mark may precede each synonym. -

Three Viable Options for a New Australian Vertical Datum
Journal of Spatial Science [submitted] THREE VIABLE OPTIONS FOR A NEW AUSTRALIAN VERTICAL DATUM M.S. Filmer W.E. Featherstone Mick Filmer (corresponding author) Western Australian Centre for Geodesy & The Institute for Geoscience Research, Curtin University of Technology, GPO Box U1987, Perth, WA 6845, Australia Telephone: +61-8-9266-2582 Fax: +61-8-9266-2703 Email: [email protected] Will Featherstone Western Australian Centre for Geodesy & The Institute for Geoscience Research, Curtin University of Technology, GPO Box U1987, Perth, WA 6845, Australia Telephone: +61-8-9266-2734 Fax: +61-8-9266-2703 Email: [email protected] Journal of Spatial Science [submitted] ABSTRACT While the Intergovernmental Committee on Surveying and Mapping (ICSM) has stated that the Australian Height Datum (AHD) will remain Australia’s official vertical datum for the short to medium term, the AHD contains deficiencies that make it unsuitable in the longer term. We present and discuss three different options for defining a new Australian vertical datum (AVD), with a view to encouraging discussion into the development of a medium- to long-term replacement for the AHD. These options are a i) levelling-only, ii) combined, and iii) geoid-only vertical datum. All have advantages and disadvantages, but are dependent on availability of and improvements to the different data sets required. A levelling-only vertical datum is the traditional method, although we recommend the use of a sea surface topography (SSTop) model to allow the vertical datum to be constrained at multiple tide-gauges as an improvement over the AHD. This concept is extended in a combined vertical datum, where heights derived from GNSS ellipsoidal heights and a gravimetric quasi/geoid model (GNSS-geoid) at discrete points are also used to constrain the vertical datum over the continent, in addition to mean sea level and SSTop constraints at tide-gauges. -
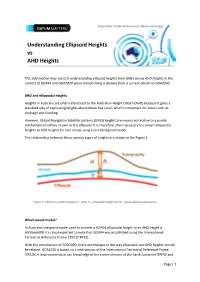
Understanding Ellipsoid Heights Vs AHD Heights
DATUM MATTERS Understanding Ellipsoid Heights vs AHD Heights This information may assist in understanding ellipsoid heights from GNSS versus AHD heights in the context of GDA94 and GDA2020 when transforming a dataset from a current datum to GDA2020. AHD and ellipsoidal heights Heights in Australia are often referenced to the Australian Height Datum (AHD) because it gives a standard way of expressing heights above Mean Sea Level, which is important for issues such as drainage and flooding. However, Global Navigation Satellite Systems (GNSS) heights are measured relative to a purely mathematical surface known as the ellipsoid. It is therefore often necessary to convert ellipsoidal heights to AHD heights (or vice versa) using a so-called geoid model. The relationship between these various types of heights are shown in the Figure 1. Figure 1: Ellipsoid vs AHD Heights (H = AHD, h = ellipsoidal height and N = geoid ellipsoid separation) Which Geoid model? In Australia, the geoid model used to convert a GDA94 ellipsoidal height to an AHD height is AUSGeoid09. It is also important to note that GDA94 was established using the International Terrestrial Reference Frame 1992 (ITRF92). With the introduction of GDA2020, there are changes to the way ellipsoidal and AHD heights should be related. GDA2020 is based on a new version of the International Terrestrial Reference Frame, ITRF2014. Improvements in our knowledge of the centre of mass of the earth, between ITRF92 and Page | 1 ITRF2014, means that an ellipsoidal height based on GDA2020 is approximately 9cm lower than one based on GDA94 (Figure 2). GDA94 GDA2020 Figure 2: A difference between an ellipsoidal height based on GDA2020 and GDA94 is approximately 9 cm. -

What Does Height Really Mean?
Department of Natural Resources and the Environment Department of Natural Resources and the Environment Monographs University of Connecticut Year 2007 What Does Height Really Mean? Thomas H. Meyer∗ Daniel R. Romany David B. Zilkoskiz ∗University of Connecticut, [email protected] yNational Geodetic Survey zNational Geodetic Suvey This paper is posted at DigitalCommons@UConn. http://digitalcommons.uconn.edu/nrme monos/1 What does height really mean? Thomas Henry Meyer Department of Natural Resources Management and Engineering University of Connecticut Storrs, CT 06269-4087 Tel: (860) 486-2840 Fax: (860) 486-5480 E-mail: [email protected] Daniel R. Roman David B. Zilkoski National Geodetic Survey National Geodetic Survey 1315 East-West Highway 1315 East-West Highway Silver Springs, MD 20910 Silver Springs, MD 20910 E-mail: [email protected] E-mail: [email protected] June, 2007 ii The authors would like to acknowledge the careful and constructive reviews of this series by Dr. Dru Smith, Chief Geodesist of the National Geodetic Survey. Contents 1 Introduction 1 1.1Preamble.......................................... 1 1.2Preliminaries........................................ 2 1.2.1 TheSeries...................................... 3 1.3 Reference Ellipsoids . ................................... 3 1.3.1 Local Reference Ellipsoids . ........................... 3 1.3.2 Equipotential Ellipsoids . ........................... 5 1.3.3 Equipotential Ellipsoids as Vertical Datums ................... 6 1.4MeanSeaLevel....................................... 8 1.5U.S.NationalVerticalDatums.............................. 10 1.5.1 National Geodetic Vertical Datum of 1929 (NGVD 29) . ........... 10 1.5.2 North American Vertical Datum of 1988 (NAVD 88) . ........... 11 1.5.3 International Great Lakes Datum of 1985 (IGLD 85) . ........... 11 1.5.4 TidalDatums.................................... 12 1.6Summary.......................................... 14 2 Physics and Gravity 15 2.1Preamble......................................... -

Set Reading Benchmarks in South Africa
SETTING READING BENCHMARKS IN SOUTH AFRICA October 2020 PHOTO: SCHOOL LIBRARY, CREDIT: PIXABAY Contract Number: 72067418D00001, Order Number: 72067419F00007 THIS PUBLICATION WAS PRODUCED AT THE REQUEST OF THE UNITED STATES AGENCY FOR INTERNATIONAL DEVELOPMENT. IT WAS PREPARED INDEPENDENTLY BY KHULISA MANAGEMENT SERVICES, (PTY) LTD. THE AUTHOR’S VIEWS EXPRESSED IN THIS PUBLICATION DO NOT NECESSARILY REFLECT THE VIEWS OF THE UNITED STATES AGENCY FOR INTERNATIONAL DEVELOPMENT OR THE UNITED STATES GOVERNMENT. ISBN: 978-1-4315-3411-1 All rights reserved. You may copy material from this publication for use in non-profit education programmes if you acknowledge the source. Contract Number: 72067418D00001, Order Number: 72067419F00007 SETTING READING BENCHMARKS IN SOUTH AFRICA October 2020 AUTHORS Matthew Jukes (Research Consultant) Elizabeth Pretorius (Reading Consultant) Maxine Schaefer (Reading Consultant) Katharine Tjasink (Project Manager, Senior) Margaret Roper (Deputy Director, Khulisa) Jennifer Bisgard (Director, Khulisa) Nokuthula Mabhena (Data Visualisation, Khulisa) CONTACT DETAILS Margaret Roper 26 7th Avenue Parktown North Johannesburg, 2196 Telephone: 011-447-6464 Email: [email protected] Web Address: www.khulisa.com CONTRACTUAL INFORMATION Khulisa Management Services Pty Ltd, (Khulisa) produced this Report for the United States Agency for International Development (USAID) under its Practical Education Research for Optimal Reading and Management: Analyze, Collaborate, Evaluate (PERFORMANCE) Indefinite Delivery Indefinite Quantity -

A Re-Evaluation of the Offset in the Australian Height Datum Between
Marine Geodesy [submitted] 1 A re-evaluation of the offset in the Australian Height 2 Datum between mainland Australia and Tasmania 3 4 M.S. FILMER AND W.E. FEATHERSTONE 5 6 Mick Filmer (corresponding author) 7 Western Australian Centre for Geodesy & The Institute for Geoscience Research, 8 Curtin University of Technology, GPO Box U1987, Perth, WA 6845, Australia 9 Telephone: +61-8-9266-2218 10 Fax: +61-8-9266-2703 11 Email: [email protected] 12 13 Will Featherstone 14 Western Australian Centre for Geodesy & The Institute for Geoscience Research, 15 Curtin University of Technology, GPO Box U1987, Perth, WA 6845, Australia 16 Telephone: +61-8-9266-2734 17 Fax: +61-8-9266-2703 18 Email: [email protected] 19 20 1 Marine Geodesy [submitted] 21 The adoption of local mean sea level (MSL) at multiple tide-gauges as a zero reference level for the 22 Australian Height Datum (AHD) has resulted in a spatially variable offset between the geoid and the 23 AHD. This is caused primarily by sea surface topography (SSTop), which has also resulted in the 24 AHD on the mainland being offset vertically from the AHD on the island of Tasmania. Errors in MSL 25 observations at the 32 tide-gauges used in the AHD and the temporal bias caused by MSL 26 observations over different time epochs also contribute to the offset, which previous studies estimate 27 to be between ~+100 mm and ~+400 mm (AHD on the mainland above the AHD on Tasmania). This 28 study uses five SSTop models (SSTMs), as well as GNSS and two gravimetric quasigeoid models, at 29 tide-gauges/tide-gauge benchmarks to re-estimate the AHD offset, with the re-evaluated offset 30 between -61 mm and +48 mm. -

Geospatial Positioning Accuracy Standards PART 4: Standards for Architecture, Engineering, Construction (A/E/C) and Facility Management
FGDC-STD-007.4-2002 NSDI National Spatial Data Infrastructure Geospatial Positioning Accuracy Standards PART 4: Standards for Architecture, Engineering, Construction (A/E/C) and Facility Management Facilities Working Group Federal Geographic Data Committee Federal Geographic Data Committee Department of Agriculture · Department of Commerce · Department of Defense · Department of Energy Department of Housing and Urban Development · Department of the Interior · Department of State Department of Transportation · Environmental Protection Agency Federal Emergency Management Agency · Library of Congress National Aeronautics and Space Administration · National Archives and Records Administration Tennessee Valley Authority Federal Geographic Data Committee Established by Office of Management and Budget Circular A-16, the Federal Geographic Data Committee (FGDC) promotes the coordinated development, use, sharing, and dissemination of geographic data. The FGDC is composed of representatives from the Departments of Agriculture, Commerce, Defense, Energy, Housing and Urban Development, the Interior, State, and Transportation; the Environmental Protection Agency; the Federal Emergency Management Agency; the Library of Congress; the National Aeronautics and Space Administration; the National Archives and Records Administration; and the Tennessee Valley Authority. Additional Federal agencies participate on FGDC subcommittees and working groups. The Department of the Interior chairs the committee. FGDC subcommittees work on issues related to data categories coordinated under the circular. Subcommittees establish and implement standards for data content, quality, and transfer; encourage the exchange of information and the transfer of data; and organize the collection of geographic data to reduce duplication of effort. Working groups are established for issues that transcend data categories. For more information about the committee, or to be added to the committee's newsletter mailing list, please contact: Federal Geographic Data Committee Secretariat c/o U.S. -

MONETARY and FINANCIAL TRENDS – SEPTEMBER 2020 Stable Financial Markets Support Economy in Recession
ANALYSIS DANMARKS NATIONALBANK 23 SEPTEMBER 2020 — NO. 17 MONETARY AND FINANCIAL TRENDS – SEPTEMBER 2020 Stable financial markets support economy in recession Calm in financial markets CONTENTS Financial markets have been calm since late March, partly due to central banks’ asset purchase programmes and liquidity measures. Financial 2 KEY TRENDS IN THE FINANCIAL conditions in Denmark are accommodative, which MARKETS helps to boost economic activity in Denmark. 3 THE ECONOMY AND FINANCIAL CONDITIONS 6 MONETARY POLICY AND MONEY Moderate strengthening MARKETS of the Danish krone 10 KRONE DEMAND AND FOREIGN Since March, the Danish krone has seen a EXCHANGE MARKETS moderate strengthening. At end-August, Dan- 11 BOND MARKETS marks Nationalbank had not intervened in the foreign exchange market in the previous five 13 EQUITY MARKETS months, and monetary policy interest rates are 16 CREDIT AND MONEY unchanged. Danmarks Nationalbank’s extra- ordinary lending facility is still being used, but to a limited extent. Low credit growth for Danish corporations Credit growth for Danish corporations has fall- en since March, while rising in the euro area. The difference can be attributed, among other factors, to the economic setback in Denmark being less severe, and to Danish corporations having built up liquidity buffers to a higher extent in the run-up to the covid-19 outbreak. ANALYSIS — DANMARKS NATIONALBANK 2 MONETARY AND FINANCIAL TRENDS – SEPTEMBER 2020 Key trends in the financial markets Since June, monetary policy interest rates in both The market development since June implies that the Denmark and the euro area have remained un- financing costs of households and non-financial cor- changed, and the money market spread has re- porations have declined further and are now leveled mained relatively stable. -

Foundational Guide to National Institutional Arrangements Instruments for Geospatial Information Management (Asia-Pacific)
United Nations committee of experts on global geospatial information management Foundational Guide to national institutional arrangements instruments for geospatial information management (Asia-Pacific) Working Group on National Institutional Arrangements August 2019 Contents UnitedEXECUTIVE SUMMARY Nations........ committee................................................................................................................... of experts on global geospatial4 infor- mation1. INTRODUCTION management .............................................................................................................................. 5 1.1 Introduction ..........................................................................................................................5 1.2 Principles for effective National Institutional Arrangements ........................................5 1.3 Description of NIA instruments .........................................................................................7 2. SELF-ASSESSMENT FRAMEWORK ...........................................................................................11 2.1 Proposed roadmap of institutional design for geospatial information management. ......11 Foundational2.2 Self-assessment checklist .................................................................................................... Guide to national12 3. GUIDE TO NIA INSTRUMENTS IN THE ASIA-PACIFIC REGION ......................................................14 institutional 3.1 Establishment of coordinating functions