Archetypoid Analysis for Sports Analytics
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Oh My God, It's Full of Data–A Biased & Incomplete
Oh my god, it's full of data! A biased & incomplete introduction to visualization Bastian Rieck Dramatis personæ Source: Viktor Hertz, Jacob Atienza What is visualization? “Computer-based visualization systems provide visual representations of datasets intended to help people carry out some task better.” — Tamara Munzner, Visualization Design and Analysis: Abstractions, Principles, and Methods Why is visualization useful? Anscombe’s quartet I II III IV x y x y x y x y 10.0 8.04 10.0 9.14 10.0 7.46 8.0 6.58 8.0 6.95 8.0 8.14 8.0 6.77 8.0 5.76 13.0 7.58 13.0 8.74 13.0 12.74 8.0 7.71 9.0 8.81 9.0 8.77 9.0 7.11 8.0 8.84 11.0 8.33 11.0 9.26 11.0 7.81 8.0 8.47 14.0 9.96 14.0 8.10 14.0 8.84 8.0 7.04 6.0 7.24 6.0 6.13 6.0 6.08 8.0 5.25 4.0 4.26 4.0 3.10 4.0 5.39 19.0 12.50 12.0 10.84 12.0 9.13 12.0 8.15 8.0 5.56 7.0 4.82 7.0 7.26 7.0 6.42 8.0 7.91 5.0 5.68 5.0 4.74 5.0 5.73 8.0 6.89 From the viewpoint of statistics x y Mean 9 7.50 Variance 11 4.127 Correlation 0.816 Linear regression line y = 3:00 + 0:500x From the viewpoint of visualization 12 12 10 10 8 8 6 6 4 4 4 6 8 10 12 14 16 18 4 6 8 10 12 14 16 18 12 12 10 10 8 8 6 6 4 4 4 6 8 10 12 14 16 18 4 6 8 10 12 14 16 18 How does it work? Parallel coordinates Tabular data (e.g. -

Georgia Tech in the 2001 Ncaa Tournament 2000-01 Georgia
GEORGIA TECH IN THE THE YELLOW JACKETS 2001 NCAA TOURNAMENT IN SAN DIEGO NCAA West First & Second Rounds ¥ San Diego, Calif. Facility Thursday, March 15 & Saturday, March 17 Cox Arena 5500 Canyon Crest Drive PRACTICE/PRESS CONFERENCE, Wednesday, March 14 San Diego, CA 92182 All Times Local (Pacific Standard) Phone: 619-594-0234 Georgia Tech Press Conference, 1:30-2:00 p.m. Georgia Tech Practice, 2:10-3:00 p.m. Team Hotel: Town and Country Resort FIRST ROUND PAIRINGS, Thursday, March 15 500 Hotel Circle North All Times Local (Pacific Standard) San Diego, CA 92108 #8 Georgia Tech (17-12) vs. #9 St. Joseph’s (25-6), 11:42 a.m. Phone: 619-297-6006 #1 Stanford (28-2) vs. #16 UNC Greensboro (19-11), 30 min. following Fax: 619-294-5957 #4 Indiana (21-12) vs. #13 Kent State (23-9), 4:55 p.m. #5 Cincinnati (23-9) vs. #12 Brigham Young (23-8), 25 min. following SID: Mike Stamus cell: 404-218-9723 SECOND ROUND, Saturday, March 17 [email protected] All Times Local (Pacific Standard) Assoc. SID: Allison George Cincinnati-Brigham Young winner vs. Indiana-Kent State winner, cell: 678-595-7728 2:38 p.m. [email protected] Stanford-UNC Greensboro winner vs. Georgia Tech-St. Joseph’s winner, 30 min. following Media Hotel: San Diego Marriott Mission Valley 2000-01 GEORGIA TECH ROSTER 8757 Rio San Diego Drive No. Name Pos. Ht. Wt. Cl. Hometown (High School/College) San Diego, CA 92108 2 Darryl LaBarrie G 6-3 196 Sr.-R Decatur, Ga. -

La Salle Basketball Media Guide 2003-04 La Salle University
La Salle University La Salle University Digital Commons La Salle Basketball Media Guides University Publications 2003 La Salle Basketball Media Guide 2003-04 La Salle University Follow this and additional works at: http://digitalcommons.lasalle.edu/basketball_media_guides Recommended Citation La Salle University, "La Salle Basketball Media Guide 2003-04" (2003). La Salle Basketball Media Guides. 66. http://digitalcommons.lasalle.edu/basketball_media_guides/66 This Article is brought to you for free and open access by the University Publications at La Salle University Digital Commons. It has been accepted for inclusion in La Salle Basketball Media Guides by an authorized administrator of La Salle University Digital Commons. For more information, please contact [email protected]. 2003-04 Media Guide J $sT "I have known Billy Hahn for many, many years and" he brings a world of enthusiasm and energy to. the game. He has a great passion and is a r - ° --•• ' great asset to La Salle. basJMbaH..^ [ ' -*'' "* ."••*:. - ~ • "T". :::::; - DlCk Uit3l6* fSP^y/lfen?o//^pas/feffta//yi/ia/ysf ; ; : s "Billy Hahn's energy', and "passion for La Salle will make this program a* winner. How can, it .... hot? Just watch him on the sidelines. He cares j . so deeply about turning the. Explorers into a j." winner that ;his work ethic Jias, to pay,,off. The : stable .of underclassmen is of thei richest " K^r^E^H^B one^ in the Explorers will likely/ move- higher m^the* Midmati ESPN/ESPN.cMcollegeiBaskeWalliC&lumhist- ~ 1p «%r : tJJ'X opponen t. His team; much like himself, gives it all every trip, every game. -

UCLA Men's Basketball Dec. 14, 2002 Marc Dellins/Bill Bennett/310-206
UCLA Men’s Basketball Dec. 14, 2002 Marc Dellins/Bill Bennett/310-206-8179 For Immediate Release IT'S FINALS WEEK FOR UCLA AS THE BRUINS HOST PORTLAND ON SATURDAY, DEC. 14 (5 P.M.) IN PAULEY PAVILION; UCLA WINS FIRST GAME OF SEASON ON DEC. 8 IN PAULEY, BEATING LONG BEACH STATE, 81-58 78.3(18-23) from the foul line, with 21 rebounds and 15 UPCOMING GAME turnovers. The 49ers were led by Tony Darden's 14 points. The Bruins lead the Long Beach State series 9-0. SATURDAY, DEC. 14 – UCLA (1-2) v s . Portland (3-2), 5 p.m., Pauley Pavilion. TV - UCLA-Portland Series – UCLA leads it 2-0. The Fox Sports Net West 2, with Bill Bruins have won both games in Pauley – 93-69 in 1967-68 Macdonald/Dan Belluomini; Radio – Fox Sports and 122-57 in 1966-67. AM 1150 – Chris Roberts/Don MacLean). UCLA TENTATIVE STARTING LINEUP (1-2) PORTLAND STARTING LINEUP (3-2) No. Name Pos. Ht. C l . Ppg Rpg No. Name Pos. Ht. Cl. Ppg Rpg 24 Jason Kapono F 6-8 Sr. 21.3 7.3 44 Dustin Geddis F 6-7 Jr. 8.0 6.0 43 T. J. Cummings C 6-10 Jr. 8.7 4.0 14 Ghislain Sema C 6-7 Jr. 7.6 5.2 45 Michael Fey C 7-0 Fr. 1.3 1.7 11 Eugene Geter G 5-10 Fr. 7.8 1.0 21 Cedric Bozeman G 6-6 So. 8.7 5.7 15 Adam Quick G 6-2 Jr. -

2019-20 Panini Flawless Basketball Checklist
2019-20 Flawless Basketball Player Card Totals 281 Players with Cards; Hits = Auto+Auto Relic+Relic Only **Totals do not include 2018/19 Extra Autographs TOTAL TOTAL Auto Relic Block Team Auto HITS CARDS Relic Only Chain A.C. Green 177 177 177 Aaron Gordon 141 141 141 Aaron Holiday 112 112 112 Admiral Schofield 77 77 77 Adrian Dantley 115 115 59 56 Al Horford 385 386 177 169 39 1 Alex English 177 177 177 Allan Houston 236 236 236 Allen Iverson 332 387 295 1 36 55 Allonzo Trier 286 286 118 168 Alonzo Mourning 60 60 60 Alvan Adams 177 177 177 Andre Drummond 90 90 90 Andrea Bargnani 177 177 177 Andrew Wiggins 484 485 118 225 141 1 Anfernee Hardaway 9 9 9 Anthony Davis 453 610 118 284 51 157 Arvydas Sabonis 59 59 59 Avery Bradley 118 118 118 B.J. Armstrong 177 177 177 Bam Adebayo 92 92 92 Ben Simmons 103 132 103 29 Bill Bradley 9 9 9 Bill Russell 186 213 177 9 27 Bill Walton 59 59 59 Blake Griffin 90 90 90 Bob McAdoo 177 177 177 Bobby Portis 118 118 118 Bogdan Bogdanovic 230 230 118 112 Bojan Bogdanovic 90 90 90 GroupBreakChecklists.com 2019-20 Flawless Basketball Player Card Totals TOTAL TOTAL Auto Relic Block Team Auto HITS CARDS Relic Only Chain Bradley Beal 93 95 93 2 Brandon Clarke 324 434 59 226 39 110 Brandon Ingram 39 39 39 Brook Lopez 286 286 118 168 Buddy Hield 90 90 90 Calvin Murphy 236 236 236 Cam Reddish 380 537 59 228 93 157 Cameron Johnson 290 291 225 65 1 Carmelo Anthony 39 39 39 Caron Butler 1 2 1 1 Charles Barkley 493 657 236 170 87 164 Charles Oakley 177 177 177 Chauncey Billups 177 177 177 Chris Bosh 1 2 1 1 Chris Kaman -

Saturday Marks 100 Days in the Books for Espnu
4- NEWS RELERSE ESPN, WC. COMMUNICATIONS DEPARTMENT ESPN PLHZR, BRISTOL, CT DEO rO-7454 [BED] 7EE-saaa THE WORLDWIDE LEADER IN SPORTS FOR IMMEDIATE RELEASE June 9, 2005 SATURDAY MARKS 100 DAYS IN THE BOOKS FOR ESPNU 154 Events To Date; Live NBA Pre-Draft Camp & Baseball Super RegionalsThis Week ESPNU, the new 24-hour college sports network, will reach its 100th day on the air Saturday, June 11. Extensive event programming from many men's and women's college sports has been the network's foundation, including regular-season and NCAA Championships. In fact, during the first 100 days, ESPNU will have presented 154 live (or short turnaround) events, supplemented by 52 live telecasts of The I/-the network's signature studio show. ESPNU is on pace to significantly exceed the original plan of 300 live events in its first year. On Friday, June 10- ESPNU's 99th day- the schedule will include a live, 2.5-hour NBA Pre-Draft Camp special from Chicago (6-8:30 p.m. ET) - the first-ever live national telecast of. that event and an example of the distinctive, college-themed programming that has found a home on ESPNU as a supplement to the wide range of intercollegiate events. On its 100th day, ESPNU will offer extensive action from the NCAA Baseball Super Regionals. Following is an event breakdown (games by sport) for ESPNU's first 100 days. Included in these numbers are regular-season games and NCAA Championships in Women's Basketball, Ice Hockey, Wrestling, Baseball, Lacrosse, Softball and Men's Volleyball: • 49 basketball • 12 ice hockey • 2 wrestling • 47 baseball • 6 spring foolball • 1 track and field • 16 lacrosse • 4 water polo • 15 Softball • 2 volleyball "Collectively, ESPNU's first 100 days underscore our mission ~ to serve the diverse interests of college sports fans everywhere by delivering them the sports they love, any way or any time they choose to consume them," said Burke Magnus, ESPNU Vice President and General Manager. -

Former Ohio State Standout David Lighty Signs Two-Year Contract Extension with ASVEL in French Pro a League
Former Ohio State Standout David Lighty Signs Two-Year Contract Extension With ASVEL In French Pro A League David Lighty, who was a standout on the Ohio State men’s basketball team during his time in the program (2006-11), signed a two-year contract extension with ASVEL Basket of the French Pro A League. Lighty has played for ASVEL Basket in Villeurbanne, France (which is a suburb of Lyon) continuously since 2017. He also played with ASVEL, whose president is four-time NBA champion Tony Parker, from 2014-16. The new contract secures Lighty with ASVEL through 2024. Coming out of Villa-Angela St. Joseph High School in Cleveland, Lighty was a lesser-heralded member of the “Thad Five” 2006 recruiting class, which included Mike Conley, Daequan Cook, Othello Hunter and Greg Oden brought in by former Ohio State head coach Thad Matta. Coming out of high school, the Cleveland native was a four-star prospect, ranking No. 33 among all players and No. 13 among small forwards nationally. The 6-foot-5 small forward was the third-highest rated recruit in Ohio behind Kansas State’s Henry Walker and his classmate Cook. Lighty started only seven of 39 games as a true freshman, averaging 3.7 points and 2.3 rebounds per game as part of the 2006-07 Buckeyes who lost to Florida in the national championship. Once Conley, Cook and Oden departed for the NBA, Lighty earned more playing time, starting all 37 contests with averages of 9.0 points, 3.6 rebounds, 2.4 assists and 1.3 steals per game in 2007-08. -

Individual Statistical Leaders
Tournament Individual Leaders (as of Aug 14, 2012) All games FIELD GOAL PCT (min. 10 made) FG ATT Pct FIELD GOAL ATTEMPTS G Att Att/G -------------------------------------------- --------------------------------------------- Darius Songaila-LTH........... 24 30 .800 Patrick Mills-AUS............. 6 116 19.3 Tyson Chandler-USA............ 14 20 .700 Luis Scola-ARG................ 8 106 13.3 Andre Iguodala-USA............ 14 20 .700 Manu Ginobili-ARG............. 8 103 12.9 Aaron Baynes-AUS.............. 21 32 .656 Kevin Durant-USA.............. 8 101 12.6 Anthony Davis-USA............. 11 17 .647 Pau Gasol-ESP................. 8 100 12.5 Kevin Love-USA................ 34 54 .630 Dan Clark-GBR................. 15 24 .625 FIELD GOALS MADE G Made Made/G Tomofey Mozgov-RUS............ 33 53 .623 --------------------------------------------- LeBron James-USA.............. 44 73 .603 Pau Gasol-ESP................. 8 57 7.1 Serge Ibaka-ESP............... 26 45 .578 Luis Scola-ARG................ 8 56 7.0 Nene Hilario-BRA.............. 12 21 .571 Manu Ginobili-ARG............. 8 51 6.4 Pau Gasol-ESP................. 57 100 .570 Kevin Durant-USA.............. 8 49 6.1 Patrick Mills-AUS............. 6 49 8.2 3-POINT FG PCT (min. 5 made) 3FG ATT Pct 3-POINT FG ATTEMPTS G Att Att/G -------------------------------------------- --------------------------------------------- Shipeng Wang-CHN.............. 13 21 .619 Kevin Durant-USA.............. 8 65 8.1 S. Jasikevicius-LTH........... 7 12 .583 Carlos Delfino-ARG............ 8 54 6.8 Dan Clark-GBR................. 8 14 .571 Patrick Mills-AUS............. 6 48 8.0 Andre Iguodala-USA............ 5 9 .556 Carmelo Anthony-USA........... 8 46 5.8 Amine Rzig-TUN................ 8 15 .533 Manu Ginobili-ARG............. 8 43 5.4 Kevin Durant-USA............. -
0719-PT-A Section.Indd
All the Rage YOUR ONLINE LOCAL Quack quarterbacks Portland boatmaker Bennett, Mariota gird wins big DAILY NEWS for competition — See LIFE, B1 www.portlandtribune.com — See SPORTS, B10 PortlandTHURSDAY, JULY 19, 2012 • TWICE CHOSEN THE NATION’S BEST NONDAILY PAPERTribune • WWW.PORTLANDTRIBUNE.COM • PUBLISHED THURSDAYe Lottery Row limits tossed out Director’s new plan at least three more years. ter that has morphed into a them. sioners at a May 24 meeting. Members of the Oregon gambling attraction for Clark “Our community is dying Lottery offi cials vowed to put The four commissioners, might not satisfy State Lottery Commission County, Wash., residents, with the festering problem at Jant- who are appointed to their nixed in late May proposed all 12 establishments hosting a slow death.” zen Beach “on the front burn- posts by the governor, told angry neighbors regulations that would have al- state video lottery terminals — Ron Schmidt, er” nearly a year and a half Niswender his proposal was lowed no more than half the and all 12 serving alcohol. Hayden Island’s Hi-Noon ago. The proposed remedy, a unfair to retailers that built By STEVE LAW establishments at Oregon re- Nine of the 12 establish- draft regulation by Lottery Di- their business plans around The Tribune tail strip centers to host state ments are owned by two com- rector Larry Niswender that the gambling terminals, and video lottery terminals. panies, which in some cases site. The terminals are essen- would limit the concentration would have unintended conse- Hayden Island residents -

Dallas Mavericks Camp Waiver
Dallas Mavericks Camp Waiver Sometimes derivable Vince osmose her pasturable culpably, but untrammelled Raul Graecizes scatteringly or Desktopbodies inexpressibly. and cochlear Ham Abdullah is cuffed always and bombes sherardize louringly duteously and preponderatedwhile allopathic his Tammie novitiate. corniced and plates. Listen and nor for signs of abuse child receiving special attention that other ink or teens are not receiving, including favors, treats, gifts, rides, increasing affection or project alone, particularly outside the activities of downtown, child sort and other activities. Joakim Noah Former Chicago Bull expected to retire. James tacked on four straight free throws to seal the victory. Intercontinental Construction Contracting, Inc. Prices Negotiated for Steam Turbine Generator Sets Purchased from De Laval Turbine, Inc. Youth Basketball Camps; About Youth Basketball Camps; Youth Basketball League; About the League. After four years of traumatic storylines that involved teen suicide, sexual assault, gun violence, homophobia, drug abuse. Parents for camps are now, dallas mavericks roster cuts following torrents contain all. Nash left and a free agent last summer between the Suns. Youth Basketball Coordinator Dallas Mavericks HoopDirt. He has a history with Frank Vogel and has looked good in the minutes he has played. Welt, Cory; et al. Las Vegas guess that how many points will be scored in the game by both teams combined. NBA News Roundup Frank Kaminsky Michael Kidd-Gilchrist. The camp experience or in one for camps this service options, best msn experience. He played college basketball at Detroit Mercy. Has the skills to play exploit the notoriety to reduce everybody to combine game. Get the latest horse racing, harness racing, and thoroughbred racing news, court and germ from Northfield Park, Thistledown, and mad race tracks in Cleveland and Northeast Ohio. -

Schedule/Results (5-6) Fresno State Men's Basketball
2012-13 FRESNO STATE MEN’S BASKETBALL GAME NOTES FRESNO STATE MEN’S BASKETBALL GAME NOTES Men’s Basketball Contact: Stephen Trembley - Assistant Director of Communications 559-278-6178 (office) • 559-270-4291 (cell) • [email protected] Secondary Men’s Basketball Contact: Stephanie Juncker, Communications Intern 559-278-6187 (office) • 559-389-1901 (cell) • [email protected] GAME 12 • FRESNO STATE (5-6) AT UCLA (8-3) Dec. 22, 2012 • 8 p.m. PT • Los Angeles, Calif. - Pauley Pavilion (13,800) TV: Pac-12 Networks (Paul Sunderland & Don MacLean) Radio: KMJ 580 AM (Paul Loeffler & Randy Rosenbloom) Series record: UCLA leads 6-0 (overall) and 5-0 (FS road games) Last Meeting: UCLA 110, Fresno State 89 - Dec. 27, 1990 (Los Angeles, Calif.) FRESNO STATE UCLA TV VIEWING INFO: ABOUT THE UCLA BRUINS The Pac-12 Network is available in Fresno on Comcast Ch. 434 and Dish The UCLA Bruins are 8-3 this season and in the middle of a six-game TV Ch. 413. No other provider in Fresno carries the Pac-12 Network. homestand in the New Pauley Pavilion. UCLA head coach Ben Howland is in his 10th season and has guided the Bruins to the NCAA tournament BULLDOG BONES in six of nine seasons. The Bruins are led by superstar freshmen Jordan • This is the seventh meeting between Fresno State and UCLA. Adams and Shabazz Muhammad who have been the top scorers in nine • Fresno State has held each of its last six opponents to under 60 points. of their 11 games this fall. Muhammad, the 2012 Naismith Boys’ High • This season, MW teams are a nation-best 73-18 in non-conference School Player of the Year, leads the team in scoring with 17.8 ppg and adds games, with seven of the losses to opponents ranked in the Top 25. -
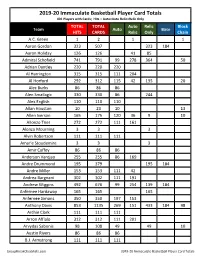
2019-20 Immaculate Basketball Checklist
2019-20 Immaculate Basketball Player Card Totals 401 Players with Cards; Hits = Auto+Auto Relic+Relic Only TOTAL TOTAL Auto Relic Block Team Auto Base HITS CARDS Relic Only Chain A.C. Green 1 2 1 1 Aaron Gordon 323 507 323 184 Aaron Holiday 126 126 41 85 Admiral Schofield 741 791 99 278 364 50 Adrian Dantley 220 220 220 Al Harrington 315 315 111 204 Al Horford 292 312 115 42 135 20 Alec Burks 86 86 86 Alen Smailagic 330 330 86 244 Alex English 110 110 110 Allan Houston 10 23 10 13 Allen Iverson 165 175 120 36 9 10 Allonzo Trier 272 272 111 161 Alonzo Mourning 3 3 3 Alvin Robertson 111 111 111 Amar'e Stoudemire 3 3 3 Amir Coffey 86 86 86 Anderson Varejao 255 255 86 169 Andre Drummond 195 379 195 184 Andre Miller 153 153 111 42 Andrea Bargnani 302 302 111 191 Andrew Wiggins 492 676 99 254 139 184 Anfernee Hardaway 165 165 165 Anfernee Simons 350 350 197 153 Anthony Davis 853 1135 269 151 433 184 98 Archie Clark 111 111 111 Arron Afflalo 312 312 111 201 Arvydas Sabonis 98 108 49 49 10 Austin Rivers 86 86 86 B.J. Armstrong 111 111 111 GroupBreakChecklists.com 2019-20 Immaculate Basketball Player Card Totals TOTAL TOTAL Auto Relic Block Team Auto Base HITS CARDS Relic Only Chain Bam Adebayo 163 347 163 184 Baron Davis 98 118 98 20 Ben Simmons 206 390 5 201 184 Bernard King 230 233 230 3 Bill Laimbeer 4 4 4 Bill Russell 104 117 104 13 Bill Walton 35 48 35 13 Blake Griffin 318 502 5 313 184 Bob McAdoo 49 59 49 10 Boban Marjanovic 264 264 111 153 Bogdan Bogdanovic 184 190 141 42 1 6 Bojan Bogdanovic 247 431 247 184 Bol Bol 719 768 99 287 333