DOCSLIB.ORG

Correlplot: a Collection of Functions for Plotting Correlation Matrices 1

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Correlplot: a Collection of Functions for Plotting Correlation Matrices 1 Correlplot: a collection of functions for plotting correlation matrices version 1.0-2 Jan Graffelman Department of Statistics and Operations Research Universitat Polit`ecnica de Catalunya Avinguda Diagonal 647, 08028 Barcelona, Spain. jan.graff[email protected] October 2013 1 Introduction This documents gives some instructions on how to create plots of correlation matrices in the statistical environment R (R Core Team, 2013) using the pack- age Correlplot. The outline of this guide is as follows: Section 2 explains how to install this package and Section 3 shows how to use the functions of the package for creating pictures like correlograms and biplots for a given correlation matrix. Computation of goodness-of-fit statistics is also illustrated. If you appreciate this software then please cite the following paper in your work: Graffelman, J. (2013) Linear-angle correlation plots: new graphs for revealing correlation structure. Journal of Computational and Graphical Statistics, 22(1) pp. 92-106. (click here to access the paper). 2 Installation The package Correlplot can be installed in R by typing: install.packages("Correlplot") library("Correlplot") This instruction will make, among others, the functions correlogram, linangplot, pco and pfa available. The correlation matrices used in the paper cited above are included in the package, and can be accessed with the data instruction. The instruction data(package="Correlplot") will give a list of all correlation and data matrices available in the package. 3 Plots of a correlation matrix In this section we indicate how to create different plots of a correlation matrix, and how to obtain the goodness-of-fit of the displays. We will subsequently treat: • The linear-angle correlation scatterplot (subsection 3.1). 1 • The principal component analysis (PCA) biplot of a correlation matrix (subsection 3.2). • The principal factor analysis biplot (PFA) of a correlation matrix (sub- section 3.3). • Correlograms of the correlation matrix (subsection 3.4). 3.1 Linear-angle correlation scatterplot An ordinary scatterplot represents two variables on orthogonal axes. A principal component analysis of two variables gives a biplot with two axes representing the two variables. If the correlation between the two variables is non-zero, then these two variable axes will be oblique. In the latter plot the angle (α) sustending the two biplot axes satisfies cos (α) = rxy, where rxy is the sample correlation coefficient between the two variables. We first illustrate this plot with Pearson and Lee's classical dataset on heights of daughters and mothers, taken from Weisberg (2005). > data(PearsonLee) > Mheight <- PearsonLee$Mheight > Dheight <- PearsonLee$Dheight > plot(Mheight,Dheight,asp=1,xlab="Mother's height (cm)", + ylab="Daughter's height (cm)",pch=19,cex=0.05) ● ● ● ● ● ● ● ● ● ● 180 ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● 170 ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● 160 ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● Daughter's height (cm) Daughter's ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● 150 ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● 140 140 150 160 170 180 Mother's height (cm) Figure 1: Scatter plot of daughter's height versus mother's height for 1375 pairs. 2 A scatterplot of the data is shown in Figure 1. Next, we create a PCA biplot of the correlation matrix, shown in Figure 2. > X <- cbind(Mheight,Dheight) > n <- nrow(X) > Xt <- scale(X)/sqrt(n-1) > res.svd <- svd(Xt) > Fs <- sqrt(n-1)*res.svd$u > Gp <- res.svd$v%*%diag(res.svd$d) > plot(Fs[,1],Fs[,2],asp=1,pch=19,cex=0.05,xlab="First principal component", + ylab="Second principal component") > arrows(0,0,3*Gp[,1],3*Gp[,2],col="red",lwd=2) > textxy(3*Gp[,1],3*Gp[,2],colnames(X),cex=1) ● ● 3 ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● 2 ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● Dheight ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● 1 ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● 0 ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● −1 ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● Mheight ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● −2 ● ● ● Second principal component ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● −3 ● ● ● ● −4 −4 −2 0 2 4 First principal component Figure 2: PCA biplot of the mother-daughter height data. The correlation between the two variable is 0.491. The angle between the two vectors in 60:61◦, and we verify cos(60:61) = 0:491. 3 Finally, we call linangplot in order to create the linear angle scatterplot shown in Figure 3 > lin.out <- linangplot(Mheight,Dheight,cex=0.05) ● ● ● ● ● 5 ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● 4 ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● 3 ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● 2 ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● 1 ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ●.
Load more

Recommended publications
  • A Generalized Linear Model for Principal Component Analysis of Binary Data
    A Generalized Linear Model for Principal Component Analysis of Binary Data Andrew I. Schein Lawrence K. Saul Lyle H. Ungar Department of Computer and Information Science University of Pennsylvania Moore School Building 200 South 33rd Street Philadelphia, PA 19104-6389 {ais,lsaul,ungar}@cis.upenn.edu Abstract they are not generally appropriate for other data types. Recently, Collins et al.[5] derived generalized criteria We investigate a generalized linear model for for dimensionality reduction by appealing to proper- dimensionality reduction of binary data. The ties of distributions in the exponential family. In their model is related to principal component anal- framework, the conventional PCA of real-valued data ysis (PCA) in the same way that logistic re- emerges naturally from assuming a Gaussian distribu- gression is related to linear regression. Thus tion over a set of observations, while generalized ver- we refer to the model as logistic PCA. In this sions of PCA for binary and nonnegative data emerge paper, we derive an alternating least squares respectively by substituting the Bernoulli and Pois- method to estimate the basis vectors and gen- son distributions for the Gaussian. For binary data, eralized linear coefficients of the logistic PCA the generalized model's relationship to PCA is anal- model. The resulting updates have a simple ogous to the relationship between logistic and linear closed form and are guaranteed at each iter- regression[12]. In particular, the model exploits the ation to improve the model's likelihood. We log-odds as the natural parameter of the Bernoulli dis- evaluate the performance of logistic PCA|as tribution and the logistic function as its canonical link.
    [Show full text]
  • Exploratory and Confirmatory Factor Analysis Course Outline Part 1
    Course Outline Exploratory and Confirmatory Factor Analysis 1 Principal components analysis Part 1: Overview, PCA and Biplots FA vs. PCA Least squares fit to a data matrix Biplots Michael Friendly 2 Basic Ideas of Factor Analysis Parsimony– common variance small number of factors. Linear regression on common factors→ Partial linear independence Psychology 6140 Common vs. unique variance 3 The Common Factor Model Factoring methods: Principal factors, Unweighted Least Squares, Maximum λ1 X1 z1 likelihood ξ λ2 Factor rotation X2 z2 4 Confirmatory Factor Analysis Development of CFA models Applications of CFA PCA and Factor Analysis: Overview & Goals Why do Factor Analysis? Part 1: Outline Why do “Factor Analysis”? 1 PCA and Factor Analysis: Overview & Goals Why do Factor Analysis? Data Reduction: Replace a large number of variables with a smaller Two modes of Factor Analysis number which reflect most of the original data [PCA rather than FA] Brief history of Factor Analysis Example: In a study of the reactions of cancer patients to radiotherapy, measurements were made on 10 different reaction variables. Because it 2 Principal components analysis was difficult to interpret all 10 variables together, PCA was used to find Artificial PCA example simpler measure(s) of patient response to treatment that contained most of the information in data. 3 PCA: details Test and Scale Construction: Develop tests and scales which are “pure” 4 PCA: Example measures of some construct. Example: In developing a test of English as a Second Language, 5 Biplots investigators calculate correlations among the item scores, and use FA to Low-D views based on PCA construct subscales.
    [Show full text]
  • A Resampling Test for Principal Component Analysis of Genotype-By-Environment Interaction
    A RESAMPLING TEST FOR PRINCIPAL COMPONENT ANALYSIS OF GENOTYPE-BY-ENVIRONMENT INTERACTION JOHANNES FORKMAN Abstract. In crop science, genotype-by-environment interaction is of- ten explored using the \genotype main effects and genotype-by-environ- ment interaction effects” (GGE) model. Using this model, a singular value decomposition is performed on the matrix of residuals from a fit of a linear model with main effects of environments. Provided that errors are independent, normally distributed and homoscedastic, the signifi- cance of the multiplicative terms of the GGE model can be tested using resampling methods. The GGE method is closely related to principal component analysis (PCA). The present paper describes i) the GGE model, ii) the simple parametric bootstrap method for testing multi- plicative genotype-by-environment interaction terms, and iii) how this resampling method can also be used for testing principal components in PCA. 1. Introduction Forkman and Piepho (2014) proposed a resampling method for testing in- teraction terms in models for analysis of genotype-by-environment data. The \genotype main effects and genotype-by-environment interaction ef- fects"(GGE) analysis (Yan et al. 2000; Yan and Kang, 2002) is closely related to principal component analysis (PCA). For this reason, the method proposed by Forkman and Piepho (2014), which is called the \simple para- metric bootstrap method", can be used for testing principal components in PCA as well. The proposed resampling method is parametric in the sense that it assumes homoscedastic and normally distributed observations. The method is \simple", because it only involves repeated sampling of standard normal distributed values. Specifically, no parameters need to be estimated.
    [Show full text]
  • GGL Biplot Analysis of Durum Wheat (Triticum Turgidum Spp
    756 Bulgarian Journal of Agricultural Science, 19 (No 4) 2013, 756-765 Agricultural Academy GGL BIPLOT ANALYSIS OF DURUM WHEAT (TRITICUM TURGIDUM SPP. DURUM) YIELD IN MULTI-ENVIRONMENT TRIALS N. SABAGHNIA2*, R. KARIMIZADEH1 and M. MOHAMMADI1 1 Department of Agronomy and Plant Breeding, Faculty of Agriculture, University of Maragheh, Maragheh, Iran 2 Dryland Agricultural Research Institute (DARI), Gachsaran, Iran Abstract SABAGHNIA, N., R. KARIMIZADEH and M. MOHAMMADI, 2013. GGL biplot analysis of durum wheat (Triticum turgidum spp. durum) yield in multi-environment trials. Bulg. J. Agric. Sci., 19: 756-765 Durum wheat (Triticum turgidum spp. durum) breeders have to determine the new genotypes responsive to the environ- mental changes for grain yield. Matching durum wheat genotype selection with its production environment is challenged by the occurrence of significant genotype by environment (GE) interaction in multi-environment trials (MET). This investigation was conducted to evaluate 20 durum wheat genotypes for their stability grown in five different locations across three years using randomized completely block design with 4 replications. According to combined analysis of variance, the main effects of genotypes, locations and years, were significant as well as the interactions effects. The first two principal components of the site regression model accounted for 60.3 % of the total variation. Polygon view of genotype plus genotype by location (GGL) biplot indicated that there were three winning genotypes in three mega-environments for durum wheat in rain-fed conditions. Genotype G14 was the most favorable genotype for location Gachsaran and the most favorable genotype of mega-environment Kouhdasht and Ilam was G12 while G10 was the most favorable genotypes for mega-environment Gonbad and Moghan.
    [Show full text]
  • A Biplot-Based PCA Approach to Study the Relations Between Indoor and Outdoor Air Pollutants Using Case Study Buildings
    buildings Article A Biplot-Based PCA Approach to Study the Relations between Indoor and Outdoor Air Pollutants Using Case Study Buildings He Zhang * and Ravi Srinivasan UrbSys (Urban Building Energy, Sensing, Controls, Big Data Analysis, and Visualization) Laboratory, M.E. Rinker, Sr. School of Construction Management, University of Florida, Gainesville, FL 32603, USA; sravi@ufl.edu * Correspondence: rupta00@ufl.edu Abstract: The 24 h and 14-day relationship between indoor and outdoor PM2.5, PM10, NO2, relative humidity, and temperature were assessed for an elementary school (site 1), a laboratory (site 2), and a residential unit (site 3) in Gainesville city, Florida. The primary aim of this study was to introduce a biplot-based PCA approach to visualize and validate the correlation among indoor and outdoor air quality data. The Spearman coefficients showed a stronger correlation among these target environmental measurements on site 1 and site 2, while it showed a weaker correlation on site 3. The biplot-based PCA regression performed higher dependency for site 1 and site 2 (p < 0.001) when compared to the correlation values and showed a lower dependency for site 3. The results displayed a mismatch between the biplot-based PCA and correlation analysis for site 3. The method utilized in this paper can be implemented in studies and analyzes high volumes of multiple building environmental measurements along with optimized visualization. Keywords: air pollution; indoor air quality; principal component analysis; biplot Citation: Zhang, H.; Srinivasan, R. A Biplot-Based PCA Approach to Study the Relations between Indoor and 1. Introduction Outdoor Air Pollutants Using Case The 2020 Global Health Observatory (GHO) statistics show that indoor and outdoor Buildings 2021 11 Study Buildings.
    [Show full text]
  • Logistic Biplot by Conjugate Gradient Algorithms and Iterated SVD
    mathematics Article Logistic Biplot by Conjugate Gradient Algorithms and Iterated SVD Jose Giovany Babativa-Márquez 1,2,* and José Luis Vicente-Villardón 1 1 Department of Statistics, University of Salamanca, 37008 Salamanca, Spain; [email protected] 2 Facultad de Ciencias de la Salud y del Deporte, Fundación Universitaria del Área Andina, Bogotá 1321, Colombia * Correspondence: [email protected] Abstract: Multivariate binary data are increasingly frequent in practice. Although some adaptations of principal component analysis are used to reduce dimensionality for this kind of data, none of them provide a simultaneous representation of rows and columns (biplot). Recently, a technique named logistic biplot (LB) has been developed to represent the rows and columns of a binary data matrix simultaneously, even though the algorithm used to fit the parameters is too computationally demanding to be useful in the presence of sparsity or when the matrix is large. We propose the fitting of an LB model using nonlinear conjugate gradient (CG) or majorization–minimization (MM) algo- rithms, and a cross-validation procedure is introduced to select the hyperparameter that represents the number of dimensions in the model. A Monte Carlo study that considers scenarios with several sparsity levels and different dimensions of the binary data set shows that the procedure based on cross-validation is successful in the selection of the model for all algorithms studied. The comparison of the running times shows that the CG algorithm is more efficient in the presence of sparsity and when the matrix is not very large, while the performance of the MM algorithm is better when the binary matrix is balanced or large.
    [Show full text]
  • Pcatools: Everything Principal Components Analysis
    Package ‘PCAtools’ October 1, 2021 Type Package Title PCAtools: Everything Principal Components Analysis Version 2.5.15 Description Principal Component Analysis (PCA) is a very powerful technique that has wide applica- bility in data science, bioinformatics, and further afield. It was initially developed to anal- yse large volumes of data in order to tease out the differences/relationships between the logi- cal entities being analysed. It extracts the fundamental structure of the data with- out the need to build any model to represent it. This 'summary' of the data is ar- rived at through a process of reduction that can transform the large number of vari- ables into a lesser number that are uncorrelated (i.e. the 'principal compo- nents'), while at the same time being capable of easy interpretation on the original data. PCA- tools provides functions for data exploration via PCA, and allows the user to generate publica- tion-ready figures. PCA is performed via BiocSingular - users can also identify optimal num- ber of principal components via different metrics, such as elbow method and Horn's paral- lel analysis, which has relevance for data reduction in single-cell RNA-seq (scRNA- seq) and high dimensional mass cytometry data. License GPL-3 Depends ggplot2, ggrepel Imports lattice, grDevices, cowplot, methods, reshape2, stats, Matrix, DelayedMatrixStats, DelayedArray, BiocSingular, BiocParallel, Rcpp, dqrng Suggests testthat, scran, BiocGenerics, knitr, Biobase, GEOquery, hgu133a.db, ggplotify, beachmat, RMTstat, ggalt, DESeq2, airway,
    [Show full text]
  • Principal Components Analysis (Pca)
    PRINCIPAL COMPONENTS ANALYSIS (PCA) Steven M. Holand Department of Geology, University of Georgia, Athens, GA 30602-2501 3 December 2019 Introduction Suppose we had measured two variables, length and width, and plotted them as shown below. Both variables have approximately the same variance and they are highly correlated with one another. We could pass a vector through the long axis of the cloud of points and a second vec- tor at right angles to the first, with both vectors passing through the centroid of the data. Once we have made these vectors, we could find the coordinates of all of the data points rela- tive to these two perpendicular vectors and re-plot the data, as shown here (both of these figures are from Swan and Sandilands, 1995). In this new reference frame, note that variance is greater along axis 1 than it is on axis 2. Also note that the spatial relationships of the points are unchanged; this process has merely rotat- ed the data. Finally, note that our new vectors, or axes, are uncorrelated. By performing such a rotation, the new axes might have particular explanations. In this case, axis 1 could be regard- ed as a size measure, with samples on the left having both small length and width and samples on the right having large length and width. Axis 2 could be regarded as a measure of shape, with samples at any axis 1 position (that is, of a given size) having different length to width ratios. PC axes will generally not coincide exactly with any of the original variables.
    [Show full text]
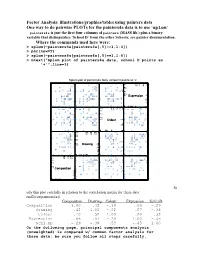
  • Factor Analysis: Illustrations/Graphics/Tables Using
    Factor Analysis: illustrations/graphics/tables using painters data One way to do pairwise PLOTs for the painters4a data is to use ‘splom’ painters4a is just the first four columns of painters (MASS lib.) plus a binary variable that distinguishes ‘School D’ from the other Schools; see painter documentation. Where the commands used here were: > splom(~painters4a[painters4a[,5]==1,1:4]) > par(new=T) > splom(~painters4a[painters4a[,5]==1,1:4]) > mtext("Splom plot of painters4a data, school D points as '+'",line=3) Splom plot of painters4a data, school D points as '+' + + ++ + 6 310 4 155 6 + + + 155 + + + + + + + + + 4 10 + + + 3 Expression 3 2 5 1 +++ + + + + + 00 1 52 3 0 + + + + 18 + + 16 10 17 15 18 15 + + + + 17 + + 10 + ++ + + 16 Colour 16 + + + 5 + + 15 + + + + + 14 0 15 5 16 14 0 + + + 18 + + 1012 1412 1614 18 + + 14 + + + + 16 1412 12 12 + 10 Drawing 10 + + + + 10 + + + + + 8 + + + + 8 ++ 6 8 8 10 1012 6 + + + + + + + + 14 1010 12 1514 15 12 + ++ + + 10 10 Composition 8 + + + + + + 5 6 + + + + + + + + 04 6 5 8 04 + + + St udy this plot carefully in relation to the correlation matrix for these data: rnd2(cor(painters4a)) Composition Drawing Colour Expression Schl.nD Composition 1.00 .42 -.10 .66 -.29 Drawing .42 1.00 -.52 .57 -.36 Colour -.10 -.52 1.00 -.20 .53 Expression .66 .57 -.20 1.00 -.45 Schl.nD -.29 -.36 .53 -.45 1.00 On the following page, principal components analysis (unweighted) is compared w/ common factor analysis for these data; be sure you follow all steps carefully. PCA results for Painters4a data The Unrotated coefficients
    [Show full text]
  • Statistics 5401 19. Biplots Gary W
    Statistics 5401 19. Biplots Gary W. Oehlert School of Statistics 313B Ford Hall 612-625-1557 [email protected] We have seen that principal components are a compact way of “approximating” data. We have seen that plotting principal components can be a useful way of visualizing data. But we have also seen that the two-dimensional plot of principal components can be a bit confusing to interpret, because it is difficult to relate back to the original variables. That is where the biplot comes in. The biplot is an enhanced plot of principal components that helps us to see connections between components and the original variables. Let be the data matrix with variable means subtracted out. We may, or may not, wish to rescale to make all the columns have unit variance; that depends on the problem. Make the svd ¢¡¤£¦¥¨§ © Begin with the first two columns of £ . Let £ ¡ £ The bivariate points are the points we plot in the usual principal components plot. § Now the first two columns of . Let § ¡ § The bivariate point tell us how the th variable enters into the first two principal components. £ § The first two columns of and along with and form a rank two approximation to ! £ § £ § )+* 658797 7977:7 07:7 " $# % (' ¡ & ¡-,.0/2143 3 where is the angle between the two-vectors and . 2 Thus large values of will occur when there is a small angle between and , and small values of will 2 2 occur when there is a large angle between and . Or put another way, positively correlated and mean than is positive, and negatively correlated and mean than is negative.
    [Show full text]
  • Biplots in Practice
    www.fbbva.es Biplots in Practice Biplots in Practice MICHAEL GREENACRE First published September 2010 © Michael Greenacre, 2010 © Fundación BBVA, 2010 Plaza de San Nicolás, 4. 48005 Bilbao www.fbbva.es [email protected] A digital copy of this book can be downloaded free of charge at http://www.fbbva.es The BBVA Foundation’s decision to publish this book does not imply any responsibility for its content, or for the inclusion therein of any supplementary documents or infor- mation facilitated by the author. Edition and production: Rubes Editorial ISBN: 978-84-923846-8-6 Legal deposit no: B- Printed in Spain Printed by S.A. de Litografía This book is produced with paper in conformed with the environmental standards required by current European legislation. In memory of Cas Troskie (1936-2010) CONTENTS Preface .............................................................................................................. 9 1. Biplots—the Basic Idea............................................................................ 15 2. Regression Biplots.................................................................................... 25 3. Generalized Linear Model Biplots .......................................................... 35 4. Multidimensional Scaling Biplots ........................................................... 43 5. Reduced-Dimension Biplots.................................................................... 51 6. Principal Component Analysis Biplots.................................................... 59 7. Log-ratio Biplots......................................................................................
    [Show full text]
  • GGE Biplot Analysis of Genotype × Environment Interaction in Chickpea Genotypes
    Available online a t www.pelagiaresearchlibrary.com Pelagia Research Library European Journal of Experimental Biology, 2013, 3(1):417-423 ISSN: 2248 –9215 CODEN (USA): EJEBAU GGE Biplot analysis of genotype × environment interaction in chickpea genotypes Ezatollah Farshadfar *1 , Mahnaz Rashidi 2, Mohammad Mahdi Jowkar 2 and Hassan Zali 1 1Campus of Agriculture and Natural Resources, Razi University, Kermanshah, Iran 2Department of agronomy and plant breeding, Kermanshah branch, Islamic Azad University, Kermanshah, Iran _____________________________________________________________________________________________ ABSTRACT The objective of this study was to explore the effect of genotype (G) and genotype × environment interaction (GEI) on grain yield of 20 chickpea genotypes under two different rainfed and irrigated environments for 4 consecutive growing seasons (2008-2011). Yield data were analyzed using the GGE biplot method. According to the results of combined analysis of variance, genotype × environment interaction was highly significant at 1% probability level, where G and GEI captured 68% of total variability. The first two principal components (PC 1 and PC 2) explained 68% of the total GGE variation, with PC 1 and PC 2 explaining 40.5 and 27.5 respectively. The first mega- environment contains environments E1, E3, E4 and E6, with genotype G17 (X96TH41K4) being the winner; the second mega environment contains environments E5, E7 and E8, with genotype G12 (X96TH46) being the winner. The environment of E2 makes up another mega-environment, with G19 (FLIP-82-115) the winner. Mean performance and stability of genotypes indicated that genotypes G4, G16 and G20 were highly stable with high grain yield. 417 Pelagia Research Library Ezatollah Farshadfar et al Euro.
    [Show full text]