The Binomial Theorem
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

An Appreciation of Euler's Formula
Rose-Hulman Undergraduate Mathematics Journal Volume 18 Issue 1 Article 17 An Appreciation of Euler's Formula Caleb Larson North Dakota State University Follow this and additional works at: https://scholar.rose-hulman.edu/rhumj Recommended Citation Larson, Caleb (2017) "An Appreciation of Euler's Formula," Rose-Hulman Undergraduate Mathematics Journal: Vol. 18 : Iss. 1 , Article 17. Available at: https://scholar.rose-hulman.edu/rhumj/vol18/iss1/17 Rose- Hulman Undergraduate Mathematics Journal an appreciation of euler's formula Caleb Larson a Volume 18, No. 1, Spring 2017 Sponsored by Rose-Hulman Institute of Technology Department of Mathematics Terre Haute, IN 47803 [email protected] a scholar.rose-hulman.edu/rhumj North Dakota State University Rose-Hulman Undergraduate Mathematics Journal Volume 18, No. 1, Spring 2017 an appreciation of euler's formula Caleb Larson Abstract. For many mathematicians, a certain characteristic about an area of mathematics will lure him/her to study that area further. That characteristic might be an interesting conclusion, an intricate implication, or an appreciation of the impact that the area has upon mathematics. The particular area that we will be exploring is Euler's Formula, eix = cos x + i sin x, and as a result, Euler's Identity, eiπ + 1 = 0. Throughout this paper, we will develop an appreciation for Euler's Formula as it combines the seemingly unrelated exponential functions, imaginary numbers, and trigonometric functions into a single formula. To appreciate and further understand Euler's Formula, we will give attention to the individual aspects of the formula, and develop the necessary tools to prove it. -

Newton and Leibniz: the Development of Calculus Isaac Newton (1642-1727)
Newton and Leibniz: The development of calculus Isaac Newton (1642-1727) Isaac Newton was born on Christmas day in 1642, the same year that Galileo died. This coincidence seemed to be symbolic and in many ways, Newton developed both mathematics and physics from where Galileo had left off. A few months before his birth, his father died and his mother had remarried and Isaac was raised by his grandmother. His uncle recognized Newton’s mathematical abilities and suggested he enroll in Trinity College in Cambridge. Newton at Trinity College At Trinity, Newton keenly studied Euclid, Descartes, Kepler, Galileo, Viete and Wallis. He wrote later to Robert Hooke, “If I have seen farther, it is because I have stood on the shoulders of giants.” Shortly after he received his Bachelor’s degree in 1665, Cambridge University was closed due to the bubonic plague and so he went to his grandmother’s house where he dived deep into his mathematics and physics without interruption. During this time, he made four major discoveries: (a) the binomial theorem; (b) calculus ; (c) the law of universal gravitation and (d) the nature of light. The binomial theorem, as we discussed, was of course known to the Chinese, the Indians, and was re-discovered by Blaise Pascal. But Newton’s innovation is to discuss it for fractional powers. The binomial theorem Newton’s notation in many places is a bit clumsy and he would write his version of the binomial theorem as: In modern notation, the left hand side is (P+PQ)m/n and the first term on the right hand side is Pm/n and the other terms are: The binomial theorem as a Taylor series What we see here is the Taylor series expansion of the function (1+Q)m/n. -

Mathematics (MATH)
Course Descriptions MATH 1080 QL MATH 1210 QL Mathematics (MATH) Precalculus Calculus I 5 5 MATH 100R * Prerequisite(s): Within the past two years, * Prerequisite(s): One of the following within Math Leap one of the following: MAT 1000 or MAT 1010 the past two years: (MATH 1050 or MATH 1 with a grade of B or better or an appropriate 1055) and MATH 1060, each with a grade of Is part of UVU’s math placement process; for math placement score. C or higher; OR MATH 1080 with a grade of C students who desire to review math topics Is an accelerated version of MATH 1050 or higher; OR appropriate placement by math in order to improve placement level before and MATH 1060. Includes functions and placement test. beginning a math course. Addresses unique their graphs including polynomial, rational, Covers limits, continuity, differentiation, strengths and weaknesses of students, by exponential, logarithmic, trigonometric, and applications of differentiation, integration, providing group problem solving activities along inverse trigonometric functions. Covers and applications of integration, including with an individual assessment and study inequalities, systems of linear and derivatives and integrals of polynomial plan for mastering target material. Requires nonlinear equations, matrices, determinants, functions, rational functions, exponential mandatory class attendance and a minimum arithmetic and geometric sequences, the functions, logarithmic functions, trigonometric number of hours per week logged into a Binomial Theorem, the unit circle, right functions, inverse trigonometric functions, and preparation module, with progress monitored triangle trigonometry, trigonometric equations, hyperbolic functions. Is a prerequisite for by a mentor. May be repeated for a maximum trigonometric identities, the Law of Sines, the calculus-based sciences. -

The Discovery of the Series Formula for Π by Leibniz, Gregory and Nilakantha Author(S): Ranjan Roy Source: Mathematics Magazine, Vol
The Discovery of the Series Formula for π by Leibniz, Gregory and Nilakantha Author(s): Ranjan Roy Source: Mathematics Magazine, Vol. 63, No. 5 (Dec., 1990), pp. 291-306 Published by: Mathematical Association of America Stable URL: http://www.jstor.org/stable/2690896 Accessed: 27-02-2017 22:02 UTC JSTOR is a not-for-profit service that helps scholars, researchers, and students discover, use, and build upon a wide range of content in a trusted digital archive. We use information technology and tools to increase productivity and facilitate new forms of scholarship. For more information about JSTOR, please contact [email protected]. Your use of the JSTOR archive indicates your acceptance of the Terms & Conditions of Use, available at http://about.jstor.org/terms Mathematical Association of America is collaborating with JSTOR to digitize, preserve and extend access to Mathematics Magazine This content downloaded from 195.251.161.31 on Mon, 27 Feb 2017 22:02:42 UTC All use subject to http://about.jstor.org/terms ARTICLES The Discovery of the Series Formula for 7r by Leibniz, Gregory and Nilakantha RANJAN ROY Beloit College Beloit, WI 53511 1. Introduction The formula for -r mentioned in the title of this article is 4 3 57 . (1) One simple and well-known moderm proof goes as follows: x I arctan x = | 1 +2 dt x3 +5 - +2n + 1 x t2n+2 + -w3 - +(-I)rl2n+1 +(-I)l?lf dt. The last integral tends to zero if Ix < 1, for 'o t+2dt < jt dt - iX2n+3 20 as n oo. -

1. More Examples Example 1. Find the Slope of the Tangent Line at (3,9)
1. More examples Example 1. Find the slope of the tangent line at (3; 9) to the curve y = x2. P = (3; 9). So Q = (3 + ∆x; 9 + ∆y). 9 + ∆y = (3 + ∆x)2 = (9 + 6∆x + (∆x)2. Thus, we have ∆y = 6 + ∆x. ∆x If we let ∆ go to zero, we get ∆y lim = 6 + 0 = 6. ∆x→0 ∆x Thus, the slope of the tangent line at (3; 9) is 6. Let's consider a more abstract example. Example 2. Find the slope of the tangent line at an arbitrary point P = (x; y) on the curve y = x2. Again, P = (x; y), and Q = (x + ∆x; y + ∆y), where y + ∆y = (x + ∆x)2 = x2 + 2x∆x + (∆x)2. So we get, ∆y = 2x + ∆x. ∆x Letting ∆x go to zero, we get ∆y lim = 2x + 0 = 2x. ∆x→0 ∆x Thus, the slope of the tangent line at an arbitrary point (x; y) is 2x. Example 3. Find the slope of the tangent line at an arbitrary point P = (x; y) on the curve y = ax3, where a is a real number. Q = (x + ∆x; y + ∆y). We get, 1 2 y + ∆y = a(x + ∆x)3 = a(x3 + 3x2∆x + 3x(∆x)2 + (∆x)3). After simplifying we have, ∆y = 3ax2 + 3xa∆x + a(∆x)2. ∆x Letting ∆x go to 0 we conclude, ∆y 2 2 mP = lim = 3ax + 0 + 0 = 3ax . x→0 ∆x 2 Thus, the slope of the tangent line at a point (x; y) is mP = 3ax . Example 4. -

Leonhard Euler: His Life, the Man, and His Works∗
SIAM REVIEW c 2008 Walter Gautschi Vol. 50, No. 1, pp. 3–33 Leonhard Euler: His Life, the Man, and His Works∗ Walter Gautschi† Abstract. On the occasion of the 300th anniversary (on April 15, 2007) of Euler’s birth, an attempt is made to bring Euler’s genius to the attention of a broad segment of the educated public. The three stations of his life—Basel, St. Petersburg, andBerlin—are sketchedandthe principal works identified in more or less chronological order. To convey a flavor of his work andits impact on modernscience, a few of Euler’s memorable contributions are selected anddiscussedinmore detail. Remarks on Euler’s personality, intellect, andcraftsmanship roundout the presentation. Key words. LeonhardEuler, sketch of Euler’s life, works, andpersonality AMS subject classification. 01A50 DOI. 10.1137/070702710 Seh ich die Werke der Meister an, So sehe ich, was sie getan; Betracht ich meine Siebensachen, Seh ich, was ich h¨att sollen machen. –Goethe, Weimar 1814/1815 1. Introduction. It is a virtually impossible task to do justice, in a short span of time and space, to the great genius of Leonhard Euler. All we can do, in this lecture, is to bring across some glimpses of Euler’s incredibly voluminous and diverse work, which today fills 74 massive volumes of the Opera omnia (with two more to come). Nine additional volumes of correspondence are planned and have already appeared in part, and about seven volumes of notebooks and diaries still await editing! We begin in section 2 with a brief outline of Euler’s life, going through the three stations of his life: Basel, St. -

The Legacy of Leonhard Euler: a Tricentennial Tribute (419 Pages)
P698.TP.indd 1 9/8/09 5:23:37 PM This page intentionally left blank Lokenath Debnath The University of Texas-Pan American, USA Imperial College Press ICP P698.TP.indd 2 9/8/09 5:23:39 PM Published by Imperial College Press 57 Shelton Street Covent Garden London WC2H 9HE Distributed by World Scientific Publishing Co. Pte. Ltd. 5 Toh Tuck Link, Singapore 596224 USA office: 27 Warren Street, Suite 401-402, Hackensack, NJ 07601 UK office: 57 Shelton Street, Covent Garden, London WC2H 9HE British Library Cataloguing-in-Publication Data A catalogue record for this book is available from the British Library. THE LEGACY OF LEONHARD EULER A Tricentennial Tribute Copyright © 2010 by Imperial College Press All rights reserved. This book, or parts thereof, may not be reproduced in any form or by any means, electronic or mechanical, including photocopying, recording or any information storage and retrieval system now known or to be invented, without written permission from the Publisher. For photocopying of material in this volume, please pay a copying fee through the Copyright Clearance Center, Inc., 222 Rosewood Drive, Danvers, MA 01923, USA. In this case permission to photocopy is not required from the publisher. ISBN-13 978-1-84816-525-0 ISBN-10 1-84816-525-0 Printed in Singapore. LaiFun - The Legacy of Leonhard.pmd 1 9/4/2009, 3:04 PM September 4, 2009 14:33 World Scientific Book - 9in x 6in LegacyLeonhard Leonhard Euler (1707–1783) ii September 4, 2009 14:33 World Scientific Book - 9in x 6in LegacyLeonhard To my wife Sadhana, grandson Kirin,and granddaughter Princess Maya, with love and affection. -
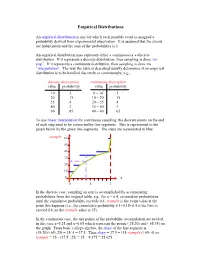
Discrete Distributions: Empirical, Bernoulli, Binomial, Poisson
Empirical Distributions An empirical distribution is one for which each possible event is assigned a probability derived from experimental observation. It is assumed that the events are independent and the sum of the probabilities is 1. An empirical distribution may represent either a continuous or a discrete distribution. If it represents a discrete distribution, then sampling is done “on step”. If it represents a continuous distribution, then sampling is done via “interpolation”. The way the table is described usually determines if an empirical distribution is to be handled discretely or continuously; e.g., discrete description continuous description value probability value probability 10 .1 0 – 10- .1 20 .15 10 – 20- .15 35 .4 20 – 35- .4 40 .3 35 – 40- .3 60 .05 40 – 60- .05 To use linear interpolation for continuous sampling, the discrete points on the end of each step need to be connected by line segments. This is represented in the graph below by the green line segments. The steps are represented in blue: rsample 60 50 40 30 20 10 0 x 0 .5 1 In the discrete case, sampling on step is accomplished by accumulating probabilities from the original table; e.g., for x = 0.4, accumulate probabilities until the cumulative probability exceeds 0.4; rsample is the event value at the point this happens (i.e., the cumulative probability 0.1+0.15+0.4 is the first to exceed 0.4, so the rsample value is 35). In the continuous case, the end points of the probability accumulation are needed, in this case x=0.25 and x=0.65 which represent the points (.25,20) and (.65,35) on the graph. -

8.6 the BINOMIAL THEOREM We Remake Nature by the Act of Discovery, in the Poem Or in the Theorem
pg476 [V] G2 5-36058 / HCG / Cannon & Elich cr 11-30-95 MP1 476 Chapter 8 Discrete Mathematics: Functions on the Set of Natural Numbers (b) Based on your results for (a), guess the minimum number of handshakes. See Exercise 19, page 469. number of moves required if you start with an arbi- Show trary number of n disks. (Hint: Tohelpseeapat- n~n 2 1! tern,add1tothenumberofmovesforn51, 2, 3, f ~n! 5 for every positive integer n. 4.) 2 (c) A legend claims that monks in a remote monastery 56. Suppose n is an odd positive integer not divisible by 3. areworkingtomoveasetof64disks,andthatthe Show that n 2 2 1 is divisible by 24. (Hint: Consider the world will end when they complete their sacred three consecutive integers n 2 1, n, n 1 1. Explain task. Moving one disk per second without error, 24 why the product ~n 2 1!~n 1 1! must be divisible by 3 hours a day, 365 days a year, how long would it take andby8.) to move all 64 disks? 57. Finding Patterns If an 5 Ï24n 1 1, (a) write out 55. Number of Handshakes Suppose there are n people the first five terms of the sequence $an%. (b) What odd at a party and that each person shakes hands with every integers occur in $an%? (c) Explain why $an% contains all other person exactly once. Let f~n! denote the total primes greater than 3. (Hint: UseExercise56.) 8.6 THE BINOMIAL THEOREM We remake nature by the act of discovery, in the poem or in the theorem. -

The Calculus of Newton and Leibniz CURRENT READING: Katz §16 (Pp
Worksheet 13 TITLE The Calculus of Newton and Leibniz CURRENT READING: Katz §16 (pp. 543-575) Boyer & Merzbach (pp 358-372, 382-389) SUMMARY We will consider the life and work of the co-inventors of the Calculus: Isaac Newton and Gottfried Leibniz. NEXT: Who Invented Calculus? Newton v. Leibniz: Math’s Most Famous Prioritätsstreit Isaac Newton (1642-1727) was born on Christmas Day, 1642 some 100 miles north of London in the town of Woolsthorpe. In 1661 he started to attend Trinity College, Cambridge and assisted Isaac Barrow in the editing of the latter’s Geometrical Lectures. For parts of 1665 and 1666, the college was closed due to The Plague and Newton went home and studied by himself, leading to what some observers have called “the most productive period of mathematical discover ever reported” (Boyer, A History of Mathematics, 430). During this period Newton made four monumental discoveries 1. the binomial theorem 2. the calculus 3. the law of gravitation 4. the nature of colors Newton is widely regarded as the most influential scientist of all-time even ahead of Albert Einstein, who demonstrated the flaws in Newtonian mechanics two centuries later. Newton’s epic work Philosophiæ Naturalis Principia Mathematica (Mathematical Principles of Natural Philosophy) more often known as the Principia was first published in 1687 and revolutionalized science itself. Infinite Series One of the key tools Newton used for many of his mathematical discoveries were power series. He was able to show that he could expand the expression (a bx) n for any n He was able to check his intuition that this result must be true by showing that the power series for (1+x)-1 could be used to compute a power series for log(1+x) which he then used to calculate the logarithms of several numbers close to 1 to over 50 decimal paces. -

Taylor Series and Mclaurin Series • Definition of a Power Series
Learning Goals: Taylor Series and McLaurin series • Definition of a power series expansion of a function at a. • Learn to calculate the Taylor series expansion of a function at a. • Know that if a function has a power series expansion at a, then that power series must be the Taylor series expansion at a. • Be aware that the Taylor series expansion of a function f(x) at a does not always sum to f(x) in an interval around a and know what is involved in checking whether it does or not. • Remainder Theorem: Know how to get an upper bound for the remainder. • Know the power series expansions for sin(x), cos(x) and (1 + x)k and be familiar with how they were derived. • Become familiar with how to apply previously learned methods to these new power series: i.e. methods such as substitution, integration, differentiation, limits, polynomial approximation. 1 Taylor Series and McLaurin series: Stewart Section 11.10 We have seen already that many functions have a power series representation on part of their domain. For example function Power series Repesentation Interval 1 1 X xn −1 < x < 1 1 − x n=0 1 1 X (−1)nxkn −1 < x < 1 1 + xk n=0 1 X xn+1 ln(1 + x) (−1)n −1 < x ≤ 1 n + 1 n=0 1 X x2n+1 ? ? arctan(x) (−1)n −1 < x < 1 2n + 1 n=0 1 X xn ex −∞ < x < 1 n! n=0 Now that you are comfortable with the idea of a power series representation for a function, you may be wondering if such a power series representation is unique and is there a systematic way of finding a power series representation for a function. -

MATHEMATICAL THEORY for SOCIAL SCIENTISTS the BINOMIAL THEOREM Pascal's Triangle and the Binomial Expansion Consider the Follo
MATHEMATICAL THEORY FOR SOCIAL SCIENTISTS THE BINOMIAL THEOREM Pascal’s Triangle and the Binomial Expansion Consider the following binomial expansions: (p + q)0 =1, (p+q)1 =p+q, (p + q)2 = p2 +2pq + q2, (p + q)3 = p3 +3p2q+3pq2 + q3, (p + q)4 = p4 +4p3q+6p2q2 +4pq3 + q4, (p + q)5 = p5 +5p4q+10p3q2 +10p2q3 +5pq4 + q5. The generic expansion is in the form of n(n 1) n(n 1)(n 2) (p + q)n =pn + npn1q + pn2q2 + pn3q3+ 2 3! n(n1) (nr+1) + pnrqr + r! n(n1)(n 2) n(n 1) + p3qn3 + p2qn2 + npqn1 + pn. 3! 2 In a tidier notation, this becomes Xn n! (p + q)n = pxqnx. (n x)!x! x=0 We can nd the coecient of the binomial expansions of successive degrees by the simple device known as Pascal’s triangle: 1 11 121 1331 14641 15101051 The numbers in each row but the rst are obtained by adding two adjacent numbers in the row above. The rule is true even for the units which border the triangle if we suppose that there are some invisible zeros extending indenitely on either side of each row. Instead of relying merely upon observation to establish the formula for the bino- mial expansion, we should prefer to derive the formula by algebraic methods. Before 1 MATHEMATICAL THEORY FOR SOCIAL SCIENTISTS we do so, we must rearm some notions concerning permutations and combinations which are essential to a proper derivation. Permutations Let us consider a set of three letters {a, b, c} and let us nd the number of ways in which they can be can arranged in a distinct order.