DOCSLIB.ORG

Darcy's Law and the Field Equations of the Flow of Underground Fluids

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Darcy's Law and the Field Equations of the Flow of Underground Fluids E DARCY'S LAW and the FIELD EQUATIONS of the FLOW of UNDERGROUND FLUIDS Downloaded from http://onepetro.org/TRANS/article-pdf/207/01/222/2176441/spe-749-g.pdf by guest on 01 October 2021 M. KING HUBBERT SHELL DEVELOPMENT CO. }AEMBER A/ME HOUSTON, TEXAS T. P. 4352 ABSTRACT by direct derivation from the Navier-Stokes equation of motion of viscous fluids. We find in this manner In 1856 Henry Darcy described in an appendix to his that: book, Les Fontaines Publiques de la Ville de Dijon, q - (Nd') (P/fL)[g - (l/p) grad p] = (TE, a series of experiments on the downward flow of water through filter sands, whereby it was estahlished that is a physical expression for Darcy's law, which is valid the rate of flow is given by the equation: for liquids generally, and for gases at pressures higher than about 20 atmospheres. Here N is a shape factor q = - K (h, - h,) /1, and d a characteristic length of the pore structure of in which q is the volume of water crossing unit area in the solid, P and fL are the density and viscosity of the unit time, I is the thickness of the sand, h, and h, fluid, (T = (Nd')(P/fL) is the volume conductivity of the heights above a reference level of the water in the system, and E = [g - (1/ p) grad p] is the impell­ manometers terminated above and below the sand, re­ ing force per unit mass acting upon the fluid. It is spectively, and K a factor of proportionality. found also that Darcy's law is valid only for flow This relationship, appropriately, soon became known velocities such that the inertial forces are negligible as compared with those arising from viscosity. as Darcy's law. Subsequently many separate attempts have been made to give Darcy's empirical expression In general, three-dimensional space there exist two a more general physical formulation, with the result superposed physical fields: a field of force of character­ istic vector E, and a field of flow of vector q. The force that so many mutually inconsistent expressions of what field is more general than the flow field since it has is purported to be Darcy's law have appeared in pub­ values in all space capable of being occupied by the lished literature that sight has often been lost of fluid. Darcy's own work and of its significance. So long as the fluid density is constant or is a func­ In the present paper, therefore, it shall be our pur­ tion of the pressure only, pose to reinform ourselves upon what Darcy himself curl E = 0, E = - grad <f> did, and then to determine the meaning of his results where when expressed explicitly in terms of the pertinent physical variables involved. This will be done first by <l> = gz + r dP. J P the empirical method used by Darcy himself, and then The field of flow, independently of the force field, must satisfy the conservation of mass, leading to the Manuscript received in Petroleum Branch office on Sept. 12, 1956. Paper prepared for presentation before Darcy Centennial Hydrology equation of continuity Symposium of the International Association of Hydrology held in Dijon. France. Sept. 2'0-26. 1956. and for dual publication as part div pq = - f op/ot of the Dijon Symposium and in the Darcy Centennial Issue of Journal of Petroleum Technology. where f is the porosity, and t is the time. For steady Discu8sion of this paper is invited. Discussion in writing (3 copies) may be sent to the office of the Journal of Petroleum motion op/ot = 0, and Technology. Any discussion offered after Dec. 31. 1956, should be in the form of a new paper. div pq = 0. PInROLEl! M TRAN~ACTIO"~. AIME 222 If the fluid is also of constant density, Appareil destine a determin ... la loi div q = O. a travers Ie sable The two fields are linked together by Darcy's law, q = aE which is physically analogous to Ohm's law in elec­ tricity. Then, when E = - grad <I', q = - a grad </' • By means of the foregoing equations the flow of both homogeneous and heterogeneous fluids through porous solids becomes amenable to the same kind of analytical treatment as is already familiar in electrical and ther­ mal conduction. The relation of Darcy's work to the development of a valid theory of the flow of fluids through porous solids, is somewhat analogous to that of Faraday to the Maxwellian equations of electromagnetism. It forms a solid experimental foundation for such a field theory, Downloaded from http://onepetro.org/TRANS/article-pdf/207/01/222/2176441/spe-749-g.pdf by guest on 01 October 2021 and the errors attributed by various recent authors to Darcy appear upon closer inspection to have been those committed by the authors themselves. INTRODUCTION In Paris in the year 1856 there was published by amnTUre Victor Dalmont as a part of the Libraire des Corps Imperiaux des Ponts et Chaussees et des Mines a mono­ graph by the French engineer Henry Darcy,' Inspector General of Bridges and Roads, bearing the title: "LES FONTAINES PUBLlQUES FIG. I-FACSIMILE OF DARCY'S ILLUSTRATION OF HIS DE LA VILLE DE DIJON EXPERIMENTAL ApPARATUS. (FROM Les Fontaines Puh­ Exposition et Application liques de la Ville de Dijon, A tlas, FIG. 3). DES PRINCIPES A SUIVRE ET DES FORMULES A EMPLOYER Dans les Questions 1. This consisted of a vertical iron pipe, 0.35 m in de diameter and 3.50 m in length (the figure shows 3.50 m DISTRIBUTION D'EAU but the text says 2.50), flanged at both ends. At a Ouvrage Termine was placed a horizontal screen supported by an iron Par un Appendice Relatif aux Fournitures height of 0.20 m above the base of the column, there d'Eau de Plusieurs Villes grillwork upon which rested a column, a meter or so AU FILTRAGE DES EAUX in length, of loose sand. Water could be admitted into et the system by means of a pipe, tapped into the column A la Fabrication des Tuyaux de Fonte, near its top, from the building water supply, and could de Plomb, de Tole et de Bitume." be discharged through a faucet from the open cham­ For several years previously M. Henry Darcy had ber near its bottom. The faucet discharged into a meas­ been engaged in modernizing and enlarging the pub­ uring tank 1 m square and 0.50 m deep, and the flow lic water works of the town of Dijon, and this treatise, rate could be controlled by means of adjustable valves comprising a 647-page volume of text and an accom­ in both the inlet pipe and the outlet faucet. panying Atlas of illustrations, constitutes an engineer­ For measuring the pressures mercury manometers ing report on that enterprise. were used, one tapped into each of the open chambers The item of present interest represents only a detail above and below the sand column. The unit of pres­ of the general work and appears in an appendix on sure employed was the meter of water and all man­ pages 590 to 594 under the heading "Determination of ometer readings were reported in meters of water meas­ the Law of Flow of Water Through Sand," and per­ ured above the bottom of the sand which was taken as tains to a problem encountered by Darcy in designing an elevation datum. The observations of the mercury a suitable filter for the system. Darcy needed to know manometers were accordingly eypressed directly in terms how large a filter would be required for a given quan­ of the heights of the water columns of equivalent water tity of water per day and, unable to find the desired manometers above a standard datum. information in the published literature, he proceeded to obtain it experimentally. The experiments comprised several series of obser­ A drawing of the apparatus used is given as Fig. 3 vations made between Oct. 29 and Nov. 2, 1855, and in the Atlas and is here reproduced in facsimile as Fig. some additional experiments made during Feb. 18 to 19, 1856. For each series the system was charged with lReferences given at end of paper. a different sand and completely filled with water. 223 VOL. 207. lYS6 By adjustment of the inlet and outlet valves the water k - dt, was made to flow downward through the sand at a e series of successively increasing rates. For each rate a k reading of the manometers was taken and recorded as a et I (h + e) = C - - t, pressure difference in meters of water above the bottom e of the sand. The results of two of these series, using [l is the logarithm to the base e.] different sands, are shown graphically in Fig. 2. In "Si la valeur ho correspond au temps to et h a un each instance it will be seen that the total rate of dis­ temps quelconque t, il viendra charge increases linearly with the drop in head across k I (h + e) = Z (h o + e) -- [t - to] ( 1 ) the sand of the two equivalent water manometers. e Darcy's own summary of the results of his experi­ "Si on remplace maintenant h + e et ho + e par ments is given in the following passage (p. 594): qe qoe '\ ' -k et -k-' 1 vlendra "Ainsi, en appelant e l'epaisseur de la couche s s de sable, s sa superficie, P la pression atmospher­ k ique, h la hauteur de l'eau sur ceUe couche, on lq = lqo -- (t - t,,) (2) aura P + h pour la pression a laquelle sera soumise e la base superieure; soient, de plus, P ± ho la pres- et les deux equations (1) et (2) donnent, soit la loi sion supportee par la surface inferieure, k un coef­ d'abaissement de la hauteur sur Ie filtre, so it la loi ficient dependant de la permeabilite de la couche q de variation des volumes debites a partir du temps t", Downloaded from http://onepetro.org/TRANS/article-pdf/207/01/222/2176441/spe-749-g.pdf by guest on 01 October 2021 Ie volume debite, on a q = k!...
Load more

Recommended publications
  • Darcy's Law Laboratory 2 HWR 531/431
    Darcy's Law Darcy's Law Laboratory 2 HWR 531/431 2-1 Darcy's Law Introduction In 1856, Henry Darcy, a French hydraulic engineer, published a report in which he described a series of experiments he had performed in an attempt to quantify the amount of water that would flow through a column of sand. The experimental apparatus used was similar to the one displayed below. Figure 1: Experimental apparatus for the illustration of Darcy's Law. (Adapted from Freeze, R.A. and Cherry, J.A., 1979) This was the first systematic study of the movement of water through a porous medium. In this setup, water is introduced to a soil column at a constant rate Q. Water exits the column at the same rate Q, creating a steady-state flow regime. Fluid pressure is measured at two points on the column, separated by a column distance Dl and a vertical distance (z1-z2). The results of Darcy's experiments indicated that the rate at which a fluid moves through a porous medium (Q) is proportional to the difference in hydraulic head of the water along the column and the characteristics of the porous medium and the column length This relationship is known as Darcy's law: dh Q = -KA dl the parameters of this equation are listed in Table 1 below: 2-2 Darcy's Law Parameter Symbol Dim Definition Discharge Q [L3/T] the amount of fluid flowing past a point per unit time Saturated K [L/T] a coefficient of proportionality describing the rate at which a Hydraulic fluid can move through a permeable medium, dependant Conductivity upon the density and viscosity of the fluid as well as the intrinsic permeability of the aquifer material.
    [Show full text]
  • A Quantitative Comparison of Some Mechanisms Generating Overpressure in Sedimentary Basins
    toyoovoS l\vC i^lt-^°°'/o62. A Quantitative Comparison of some Mechanisms Generating Overpressure in Sedimentary Basins Institutt for energiteknikk Institute for Energy Technology A quantitative comparison of some mechanisms generating overpressure sedimentary basins Magnus Wangen Institute for Energy Technology Box 40 N-2007 Kjeller NORWAY e-mail: [email protected] tel: +47-6380-6259 fax: +47-6381-5553 Submitted October 30, 2000 Revised Mars 7, 2001 DISCLAIMER Portions of this document may be illegible in electronic image products. Images are produced from the best available original document. Performing Organisation Document no.: Date Institutt for energiteknikk IFE/KR/E-2001/002 2001-05-18 Kjeller Project/Contract no. and name Client/Sponsor Organisation and reference: Title and subtitle A Quantitative Comparison of some Mechanisms Generating Overpressure in Sedimentary Basins Authors) l\/j. 1 \ Reviewed >0 Approved Magnus Wan^cnj (j Tom Pedersen Tor Bjdmstad Abstract Expulsion of fluids in low permeable rock generate overpressure. Several mechanisms are suggested for fluid expulsion and overpressure build-up, and some of them have here been studied and compared. These are mechanical compaction, aquathermal pressuring, dehydration of clays, hydrocarbon generation and cementation of the pore space. A single pressure equation for these fluid expulsion processes has been studied. In particular, the source term in this pressure equation is studied carefully, because the source term consists of separate terms representing each mechanism for pressure build-up. The amount of fluid expelled from each mechanism is obtained from these individual contributions to the source term. It is shown that the rate of change of porosity can be expressed in at least two different ways for dehydration reactions and oil generation.
    [Show full text]
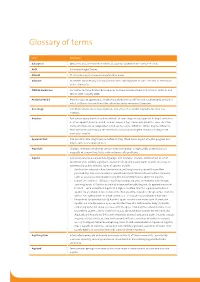
  • Glossary of Terms
    Glossary of terms Item Definition Adsorption Attraction and adhesion of ions from an aqueous solution to the surface of solids. AHD Australian Height Datum. Alluvial Of, or pertaining to, material transported by water. Alluvium Sediments deposited by, or in conjunction with, running water in rivers, streams or sheet wash and in alluvial fans. ANZECC Guidelines Australian and New Zealand Environment and Conservation Council's Guidelines for Fresh and Marine Water Quality 2000. Analytical Model Provides exact or approximate mathematical solution to a differential equation (and associated initial and boundary conditions) for subsurface water movement/transport. Anisotropy Conditions where one or more hydraulic properties of an aquifer vary with direction (see Isotropy). Anticline Fold convex upward or had such an attitude at some stage of development. In simple anticlines, beds are oppositely inclined while in more complex types limbs may dip in the same direction. Some anticlines are so complicated as to have no simple definition. Others may be defined as folds with older rocks toward the centre of curvature, providing the structural history is not unusually complex. Appraisal Well CSG well drilled for long-term production testing. Stand-alone or part of a pilot program and may become a development well. Aquiclude Geologic formation which may contain water (sometimes in appreciable quantities) but is incapable of transmitting fluids under ordinary field conditions. Aquifer (a) Consolidated or unconsolidated geologic unit (material, stratum, or formation) or set of connected units yielding significant quantities of suitable quality water to wells or springs in economically usable amounts. Types of aquifers include: • Confined (or artesian) – Aquifer overlain by confining layer or aquitard (layer of low permeability) that restricts water's upward movement.
    [Show full text]
  • Darcy Tools Version 3.4 – User's Guide
    Darcy Tools versionDarcy 3.4 Tools – User’s Guide R-10-72 Darcy Tools version 3.4 User’s Guide Urban Svensson, Computer-aided Fluid Engineering AB Michel Ferry, MFRDC, Orvault, France December 2010 Svensk Kärnbränslehantering AB Swedish Nuclear Fuel and Waste Management Co Box 250, SE-101 24 Stockholm Phone +46 8 459 84 00 R-10-72 CM Gruppen AB, Bromma, 2011 CM Gruppen ISSN 1402-3091 Tänd ett lager: SKB R-10-72 P, R eller TR. Darcy Tools version 3.4 User’s Guide Urban Svensson, Computer-aided Fluid Engineering AB Michel Ferry, MFRDC, Orvault, France December 2010 This report concerns a study which was conducted for SKB. The conclusions and viewpoints presented in the report are those of the authors. SKB may draw modified conclusions, based on additional literature sources and/or expert opinions. A pdf version of this document can be downloaded from www.skb.se. Preface The User’s Guide for DarcyTools V3.4 is intended to assist new and experienced users of DarcyTools. The Guide is far from complete and it has not been the ambition to write a manual that answers all questions a user may have. The objectives of the Guide can be stated as follows: – Give an overview of the code structure and how DarcyTools is used. – Get familiar with the “Compact Input File”, which is the main way to specify input data. – Get familiar with the “Fortran Input File”, which is the more advanced way to specify input data. R-10-72 3 Contents 1 Introduction 7 1.1 Background 7 1.2 Objective 7 1.3 Intended use and user 7 1.4 Outline 8 2 What DarcyTools does 9 2.1
    [Show full text]
  • Introduction to Reservoir Simulation As Practiced in Industry
    Introduction to Reservoir Simulation as Practiced in Industry Knut{Andreas Lie SINTEF Digital, Mathematics and Cybernetics / Department of Mathematical Sciences, NTNU, Norway Computational Issues in Oil Field Applications Tutorials March 21{24, 2017, IPAM, UCLA 1 / 52 Petroleum reservoirs Naturally occurring flammable liquid/gases found in geological formations I Originating from organic sediments that have been compressed and 'cooked' to form hydrocarbons that migrated upward in sedimentary rocks until limited by a trapping structure I Found in shallow reservoirs on land and deep under the seabed I Only 30% of the reserves are 'conventional'; remaining 70% include shale oil and gas, heavy oil, extra heavy oil, and oil sands. Uses of (refined) petroleum: I Fuel (gas, liquid, solid) I Alkenes manufactured into plastics and compounds I Lubricants, wax, paraffin wax I Pesticides and fertilizers for Johan Sverdrup, new Norwegian 'elephant' discovery, 2011. agriculture Expected to be producing for the next 30+ years 2 / 52 Production processes Gas Oil Caprock Aquifer w/brine Primary production { puncturing the 'balloon' When the first well is drilled and opened for production, trapped hydrocarbon starts flowing toward the well because of over-pressure 3 / 52 Production processes Gas injection Gas Oil Water injection Secondary production { maintaining reservoir flow As pressure drops, less hydrocarbon is flowing. To maintain pressure and push more profitable hydrocarbons out, one starts injecting water or gas into the reservoir, possibly in an alternating fashion from the same well. 3 / 52 Production processes Gas injection Gas Oil Water injection Enhanced oil recovery Even more crude oil can be extracted by gas injection (CO2, natural gas, or nitrogen), chemical injection (foam, polymer, surfactants), microbial injection, or thermal recovery (cyclic steam, steam flooding, in-situ combustion), etc.
    [Show full text]
  • Chapter 4 Volumetric Flux
    Chapter 4 Volumetric Flux We have so far talked about Darcy's law as if it was one of the fundamental laws of nature. Here we will first describe the original experiment by Darcy in 1856. We will then generalize to cases where the flow is in more than one dimension. Finally we will identify common cases when the displacement does not follow Darcy's law. Darcy's Experiment (Bear 1972) In 1856, Henry Darcy investigated the flow of water in vertical homogeneous sand filters in connection with the fountains of the city of Dijon, France. Fig. 4.1 shows the experimental set-up he employed. From his experiments, Darcy concluded that the rate of flow (volume per unit time) q is (a) proportional to the constant cross- sectional area A, (b) proportional to (h1 - h2), and inversely proportional to the length L. When combined, these conclusions give the famous Darcy formula: qKAhh=−() L 12 Fig. 4.1 Darcy's experiment (Bear 1972) where K is the hydraulic conductivity. The pressure drop across the pack was measured by the height of the water levels in the manometer tubes. This difference in water levels is known as the hydraulic or piezometric head across the pack and is expressed in units of length rather than units of pressure. It is a measure of the departure from hydrostatic conditions across the pack. Flow Potential The hydraulic head was convenient when pressures were measured by manometers or standpipes and only one fluid is flowing. It is more useful for multidimensional, multiphase fluid flow to define a flow potential for each phase.
    [Show full text]