Signal Theory - Alexander M
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

UNDER GRADUATE PROGRAMME B.Tech
CURRICULUM UNDER GRADUATE PROGRAMME B.Tech. NATIONAL INSTITUTE OF TECHNOLOGY KARNATAKA, SURATHKAL SRINIVASNAGAR PO, MANGALORE – 575 025 KARNATAKA, INDIA Phone: +91-824-2474000 Web-Site: www.nitk.ac.in Fax : +91-824 –2474033 2012 NATIONAL INSTITUTE OF TECHNOLOGY KARNATAKA, SURATHKAL ---------------------------------------------------------- MOTTO * Work is Worship VISION * To Facilitate Transformation of Students into- Good Human Beings, Responsible Citizens and Competent Professionals, focusing on Assimilation, Generation and Dissemination of Knowledge. MISSION * Impart Quality Education to Meet the Needs of Profession and Society and Achieve Excellence in Teaching-Learning and Research. * Attract and Develop Talented and Committed Human Resource and Provide an Environment Conducive to Innovation, Creativity, Team-spirit and Entrepreneurial Leadership * Facilitate Effective Interactions Among Faculty and Students and Foster Networking with Alumni, Industries, Institutions and Other Stake-holders. * Practice and Promote High Standards of Professional Ethics, Transparency and Accountability. CURRICULUM UNDER GRADUATE PROGRAMMES 2012 NATIONAL INSTITUTE OF TECHNOLOGY KARNATAKA, SURATHKAL ---------------------------------------------------------- CURRICULUM 2012 UNDER GRADUATE PROGRAMME B.Tech. SECTIONS 1. Regulations (General) 2. Regulations – UG 3. Forms & Formats – UG 4. Course Structure – UG 5. Course Contents – UG ------------------------------------------------------------------------------- NITK- UG- Curriculum 2012 NATIONAL INSTITUTE -

Program 2009 V1.11.Pub
Long Island Section 2009 Annual Awards Ceremony MESSAGE FROM THE CHAIRMAN IEEE Colleagues and Friends: I am delighted to welcome everyone to the 2009 IEEE Long Island Section’s Awards Banquet. This is a special year as we are celebrating the 125th Anniversary of the IEEE. Tonight we will be presenting awards in several categories. This year Long Island members will be receiving national, regional, and local awards. The IEEE uses these awards to recognize its members for their outstanding accomplishments. This year, three Long Island members were awarded the prestigious IEEE Fellow Award. Long Island members were also awarded eight IEEE Region 1 awards. It is clear that the members of the Long Is- land Section continue to demonstrate the excellent quality of their capabilities and character. We will also be taking time tonight to thank the section volunteers. All of us can be proud of the efforts expended by the people on our Executive Committee (ExCOM). The ExCOM members toil for many hours in order to provide such IEEE services including technical lectures and professional development events to the members of the Long Island Section. I would like to thank Jon Garruba and Nick Golas for arranging this year’s Awards Banquet. They have now joined the select group of people who have been Awards Banquet organizers and they now know what it takes to arrange an event like this. It may come in handy when their children are getting married. I would also like to thank the Awards Committee headed by Jesse Taub in their impor- tant task of selecting and advocating tonight’s awardees. -

The 2019 IEEE Long Island Section Annual Banquet Program
2019 KEYNOTE ADDRESS INSIDE THE THURSDAY, MARCH 28, 2019 BLACK BOX: CREST HOLLOW COUNTRY CLUB, WHAT'S REALLY WOODBURY, NEW YORK HAPPENING IN DR. JOHN S. NADER 5:30 - 7:00 PM GUEST ARRIVAL, HORS D'OEUVRES President, Farmingdle UNDERGRADUATE State College 7:00 - 7:10 PM CALL TO ORDER EDUCATION? 7:10 - 7:25 PM KEYNOTE ADDRESS and WELCOME 7:25 - 7:35 PM IEEE LI OFFICER RECOGNITION AWARDS Dr. John S. Nader became President of Farmingdale State College 7:35 - 8:00 PM LONG ISLAND SECTION AWARDS in July 2016. Since arriving, he has focused on the development Alex Gruenwald Award of new academic programs, building partnerships with private Mr. Louis D’Onofrio , Consultant industries and community colleges, advancing applied learning Harold Wheeler Award opportunities, expanding support for student scholarships, improving Mr. Paul O’Connor , student services, and enhancing building and grounds. Under his Brookhaven National Laboratories guidance, the College recently adopted a new strategic plan and Ms. Catherine McNally , Telephonics Corporation mission statement. Lifetime Achievement Award As president, Dr. Nader has initiated numerous aesthetic improve- Mr. Kenneth Short , Stony Brook University ments to the Farmingdale campus. Flags representing the home countries of FSC’s increasingly international student population are Charles Hirsch Award Mr. Paul Molnar , now incorporated into Ralph Bunche Plaza to recognize the Telephonics Corporation national origin of Farmingdale graduates. Dr. Nader celebrates student artwork with a display in his home. Athanasios Papoulis Outstanding Educator Award Dr. Steven Zhivun Lu , Farmingdale now enrolls over 10,000 students and has experi - New York Institute of Technology enced the highest enrollment growth in the SUNY system over the Outstanding Young Engineer Award past several years. -

Estimation, Detection, and Identification CMU 18752
Estimation, Detection, and Identification CMU 18752 Graduate Course on the CMU/Portugal ECE PhD Program Spring 2008/2009 Instructor: Prof. Paulo Jorge Oliveira pjcro @ isr.ist.utl.pt Phone: +351 21 8418053 ou 2053 (inside IST) PO 0809 Detection, Estimation, and Filtering Graduate Course on the CMU/Portugal ECE PhD Program Spring 2008/2009 Instructor: Prof. Paulo Jorge Oliveira pjcro @ isr.ist.utl.pt Phone: +351 21 8418053 ou 2053 (inside IST) PO 0809 Objectives: • Motivation for estimation, detection, filtering, and identification in stochastic signal processing • Methodologies on design and synthesis of optimal estimation algorithms • Characterization of estimators and tools to study their performance • To provide an overview in all principal estimation approaches and the rationale for choosing a particular technique Both for parameter and state estimation, always on the presence of stochastic disturbances In RADAR (Radio Detection and Ranging), SONAR (sound navigation and ranging), speech, image, sensor networks, geo-physical sciences,… PO 0809 Pre-requisites: • Random Variables and Stochastic Processes Joint, marginal, and conditional probability density functions: ; Gaussian / normal distributions; Moments of random variables (mean and variance); Wide-sense stationary processes; Correlation and covariance; Power spectral density; • Linear Algebra Vectors: orthogonality, linear independence, inner product; norms; Matrices: eigenvectors, rank, inverse and pseudo-inverse; • Linear Systems LTIS and LTVs; ODEs and solutions; Response of linear systems; Transition matrix; Observability and controlability; Lyapunov stability. The implementation of solutions for problems require the use of MATLAB and Simulink. PO 0809 Syllabus: Classical Estimation Theory Chap. 1 - Motivation for Estimation in Stochastic Signal Processing [1/2 week] Motivating examples of signals and systems in detection and estimation problems; Chap. -

Department of Electrical and Electronics Engineeing NITK Surathkal
Department of Electrical and Electronics Engineeing NITK Surathkal ------------------------------------------------------------------------------------------------------------------------------- UG Programme: B. Tech. in Electrical and Electronics Engineering Course Details 1. Course Code: EE101 Course Title: Analysis of Electric Circuits (L -T-P) Credits: (3-1-0)4 Course Outcomes (COs): CO-1: Ability to analyse the electrical networks for the given excitation. CO-2: Ability to reduce the complex network into simpler form for analysis. CO-3: Ability to solve the three phase electrical networks for unknown parameters. CO-4: Ability to apply the mathematical techniques for solving the differential equations of electrical networks. Syllabus: Review of network geometry and network reduction techniques. Network theorems. Network variables, identification of the number of degrees of freedom, the concept of order of a system, establishing the equilibrium equations, network modeling based on energy-indicating (state) variables in the standard form, natural frequencies and natural response of a network. Introduction to system functions, inclusion of forcing functions, solution methodology to obtain complete solution in the time- domain – the vector-matrix approach. Analysis of network response (in the timedomain) for mathematically describable excitations. Solution strategy for periodic excitations. The phenomenon of resonance and its mathematical analysis. Sinusoidal steady state analysis. Introduction to three-phase systems. Magnetic circuit -

Curriculum Vitae-Thomas Kailath Hitachi America Professor Of
Curriculum Vitae-Thomas Kailath Hitachi America Professor of Engineering, Emeritus Information Systems Laboratory, Dept. of Electrical Engineering Stanford, CA 94305-9510 USA Tel: (650) 494-9401 Email: [email protected], [email protected] Home page: www.stanford.edu/~tkailath Fields of Interest: Information Theory, Communication, Computation, Control, Linear Systems, Statistical Signal Processing, VLSI Systems, Semiconductor Manufacturing and Lithography, Probability, Statistics, Linear Algebra, Matrix and Operator Theory. Born in Poona (now Pune), India, June 7, 1935. In the US since 1957; naturalized: June 8, 1976 B.E. (Telecom.), College of Engineering, Pune, India, June 1956 S.M. (Elec. Eng.), Massachusetts Institute of Technology, June, 1959 Thesis: Sampling Models for Time-Variant Filters Sc.D. (Elec. Eng.), Massachusetts Institute of Technology, June 1961 Thesis: Communication via Randomly Varying Channels Positions Sep 1957- Jun 1961 : Research Assistant, Research Laboratory for Electronics, MIT Oct 1961- Dec 1962 : Communications Research Group, Jet Propulsion Labs, Pasadena, CA; also Visiting Asst. Professor at Caltech Jan 1963- Aug 1964 : Acting Assoc. Prof. of Elec. Eng., Stanford University ( on paid leave at UC Berkeley, Jan-Aug, 1963) Sep 1964- Jan 1968 : Associate Professor of Elec. Eng. Jan 1968- Feb 1968 : Full Professor of Elec. Eng. Feb 1988- Jun 2001 : First holder of the Hitachi America Professorship in Engineering July 2001- Present : Hitachi America Professorship in Engineering, Emeritus; recalled to active duty to continue his research and writing activities. He has also held shorter-term appointments at several institutions around the world: UC Berkeley (1963), Indian Statistical Institute (1966), Bell Labs (1969), Indian Institute of Science (1969-70, 1976, 1993, 1994, 2000, 2002), Cambridge University (1977), K. -

(CSE) Bachelor of Technology in Computer Science & Engineering
NATIONAL INSTITUTE OF TECHNOLOGY, GOA --------------------------------------------------------------------------------------------------------------------- Department of Computer Science & Engineering (CSE) Bachelor of Technology in Computer Science & Engineering Foundation Courses (Fndn) MA100 Engineering Mathematics – I (3-1-0) 4 Programme Specific Electives (PSE) MA101 Engineering Mathematics – II (3-1-0) 4 CS400 Object Oriented Programming (3-0-0) 3 PH100 Physics (3-0-0) 3 CS401 Information Systems (3-0-0) 3 PH101 Physics Lab (0-0-3) 1 CS402 Object Oriented Analysis & Design (3-1-0) 4 CY100 Chemistry (3-0-0) 3 CS403 Advanced Data Structures (3-1-0) 4 CY101 Chemistry Lab (0-0-3) 1 CS404 Computer Vision (3-0-0) 3 CV100 Engineering Mechanics (3-1-0) 4 CS405 Advance Computer Architecture (3-1-0) 4 EE100 Elements of Electrical Engg (3-1-0) 4 CS406 Advanced Microprocessors (3-0-0) 3 EC100 Elements of Electronics and CS407 Optimization Techniques in Computing (3-1-0) 4 Communication Engg. (3-1-0) 4 CS408 Artificial Intelligence (3-0-0) 3 ME100 Elements of Mechanical Engg. (3-0-0) 3 CS409 Multimedia and Virtual Reality (3-0-0) 3 ME101 Engineering Graphics (1-0-3) 2 CS410 Advanced Database Systems (3-1-0) 4 ME102 Workshop (0-0-3) 1 CS411 Data Warehousing and Data Mining (3-1-0) 4 CS100 Computer Programming (3-0-0) 3 CS412 Soft Computing (3-0-0) 3 CS101 Computer Programming Lab (0-0-3) 1 CS413 Number Theory and Cryptography (3-1-0) 4 HU100 Professional Communication (3-1-0) 4 CS414 Applied Algorithms (3-1-0) 4 HU300 Engineering Economics (3-1-0) -

WIRELESS COMMUNICATIONS and NETWORKING 0.976 an Overview of EURASIP Journals 13
EURASIP NEWS LETTER ISSN 1687-1421, Volume 20, Number 3, September 2009 European Association for Signal Processing Newsletter, Volume 20, Number 3, September 2009 Contents EURASIP MESSAGES President’sMessage...................................... 1 FourNewEURASIPFellowsElected............................. 3 EURASIPMessageLiaison.................................. 7 TheEURASIPPhDDatabase-Rejuvenated......................... 11 AnOverviewofEURASIPJournals............................. 12 EURASIP Awards Presented at EUSIPCO 2009 . ........... 16 EURASIP CO-SPONSORED EVENTS WorkshopandConferenceActivities............................ 18 CalendarofEvents....................................... 19 Workshop on Content Based Multimedia Indexing (CBMI 2009) . ........... 20 Report on International Workshop on Cross-Layer Design (IWCLD09) . 22 Report on CROWNCOM 2009, June 22–24, 2009 . ........... 23 16th International Workshop on Systems, Signals and Image Processing (IWSSIP 2009), 18–20 JUNE 2009, Chalkida, Greece . 24 Report on 13th International Conference “Speech and Computer” SPECOM-2009 . 25 Call for Papers: 6th International Symposium on Image and Signal Processing and Analysis (ISPA 2009) ..................................... 28 Call for Papers: The second IAPR international workshop on Cognitive Information Processing (CIP2010) . ........... 29 Call for Papers: Fourth International Conference on Image and Signal Processing (ICISP 2010) . ........................ 30 Call for Papers: 19th European Signal Processing Conference (EUSPICO 2011) -
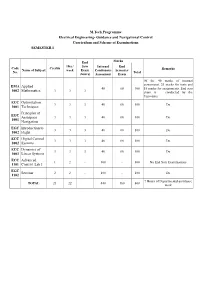
Electrical , Guidance and Navigational Control
M.Tech Programme Electrical Engineering- Guidance and Navigational Control Curriculum and Scheme of Examinations SEMESTER I End Marks Hrs / Sem Internal End Code Credits Remarks Name of Subject week Exam Continuous Semester No. Total (hours) Assessment Exam Of the 40 marks of internal EMA Applied assessment, 25 marks for tests and 40 60 100 15 marks for assignments. End sem 1002 Mathematics 3 3 3 exam is conducted by the University ECC Optimization 3 3 3 40 60 100 Do 1001 Techniques Principles of EGC Aerospace 3 3 3 40 60 100 Do 1001 Navigation EGC Introduction to 3 3 3 40 60 100 Do 1002 Flight ECC Digital Control 3 3 3 40 60 100 Do 1002 Systems ECC Dynamics of 3 3 3 40 60 100 Do 1003 Linear Systems ECC Advanced 1 2 - 100 - 100 No End Sem Examinations 1101 Control Lab I EGC Seminar 2 2 - 100 - 100 Do 1102 7 Hours of Departmental assistance TOTAL 21 22 440 360 800 work SEMESTER II End Marks Hrs / Sem Internal End Code Name of Credits week Exam Continuous Semester Remarks No. Subject Total (hours) Assessment Exam Of the 40 marks of internal assessment, 25 marks for Optimal ECC2 tests and 15 marks for Control 3 3 3 40 60 100 001 assignments. End sem exam Theory is conducted by the University Guidance and EGC Control of 3 3 3 40 60 100 Do 2001 Missiles Stream ** 3 3 3 40 60 100 Do Elective I Stream ** 3 3 3 40 60 100 Do Elective II Department ** 3 3 3 40 60 100 Do Elective ECC Research End Sem Exam is conducted 2 2 3 40 60 100 2000 Methodology by the Individual Institutions ECC Advanced 1 2 - 100 100 No End Sem Examinations 2101 Control Lab -

Advanced Control Systems Detection, Estimation, and Filtering
Advanced Control Systems Detection, Estimation, and Filtering Graduate Course on the MEng PhD Program Spring 2012/2013 Instructor: Prof. Paulo Jorge Oliveira [email protected] or pjcro @ isr.ist.utl.pt Phone: 21 8419511 or 21 8418053 (3511 or 2053 inside IST) PO 1213 Objectives: • Motivation for estimation, detection, filtering, and identification in stochastic signal processing • Methodologies on design and synthesis of optimal estimation algorithms • Characterization of estimators and tools to study their performance • To provide an overview in all principal estimation approaches and the rationale for choosing a particular technique Both for parameter and state estimation, always on the presence of stochastic disturbances In RADAR (Radio Detection and Ranging), SONAR (sound navigation and ranging), speech, image, sensor networks, geo-physical sciences,… PO 1213 Pre-requisites: • Random Variables and Stochastic Processes Joint, marginal, and conditional probability density functions: Gaussian / normal distributions; Moments of random variables (mean and variance); Wide-sense stationary processes; Correlation and covariance; Power spectral density; • Linear Algebra Vectors: orthogonality, linear independence, inner product; norms; Matrices: eigenvectors, rank, inverse, and pseudo-inverse; • Linear Systems LTIS and LTVs; ODEs and solutions; Response of linear systems; Transition matrix; Observability and controlability; Lyapunov stability. The implementation of solutions for problems require the use of MATLAB and Simulink. PO 1213 -
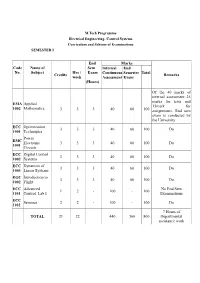
Code No. Name of Subject Credits Hrs / Week End Sem Exam (Hours)
M.Tech Programme Electrical Engineering- Control Systems Curriculum and Scheme of Examinations SEMESTER I End Marks Code Name of Sem Internal End No. Subject Hrs / Exam Continuous Semester Total Credits Remarks week Assessment Exam (Hours) Of the 40 marks of internal assessment 25 marks for tests and EMA Applied 15mark for 1002 Mathematics 3 3 3 40 60 100 assignments. End sem exam is conducted by the University ECC Optimization 3 3 3 40 60 100 Do 1001 Techniques Power EMC Electronic 3 3 3 40 60 100 Do 1001 Circuits ECC Digital Control 3 3 3 40 60 100 Do 1002 Systems ECC Dynamics of 3 3 3 40 60 100 Do 1003 Linear Systems EGC Introduction to 3 3 3 40 60 100 Do 1002 Flight ECC Advanced No End Sem 1 2 - 100 - 100 1101 Control Lab I Examinations ECC Seminar 2 2 - 100 - 100 Do 1102 7 Hours of TOTAL 21 22 440 360 800 Departmental assistance work SEMESTER II End Marks Code Name of Sem Internal End Hrs / No. Subject Credits Exam Continuous Semester Total Remarks week Assessment Exam (hours) Of the 40 marks of internal assessment, 25 marks for tests and 15 ECC Optimal Control 3 3 3 40 60 100 marks for assignments. 2001 Theory End sem exam is conducted by the University ECC Non Linear 3 3 3 40 60 100 Do 2002 Control Systems Stream Elective ** 3 3 3 40 60 100 Do I Stream Elective ** 3 3 3 40 60 100 Do II Department ** 3 3 3 40 60 100 Do Elective End Sem Exam is ECC Research 2 2 3 40 60 100 conducted by the 2000 Methodology Individual Institutions ECC Advanced No End Sem 1 2 - 100 100 2101 Control Lab II Examinations ECC Seminar 2 2 - 100 100 do 2102 -

Additional Information About This Event And
MESSAGE FROM THE LONG ISLAND SECTION CHAIRMAN Dear IEEE Colleagues, Honorees, and Friends: Welcome to the 201IEEE -POH*TMBOE4FDUJPO"XBSETCeremony! Tonight we have a chance to honor some of the IEEE members among us who have excelled. Our Long Island Section has a long and distinguished history of producing key contributions to the profession and to society and this proud tradition is carried on through the exemplary work of the awardees. This year, Section members and Organizations received five Region 1 Awards, nine IEEE Long Island Section Awards, and an Award from the IEEE Educational Activities Board (RAB). We will also take some time this evening to recognize our volunteers whose efforts energize the Section. It’s through their work that the Section’s many events and activities are possible. I would like to personally thank the entire Executive Committee (ExCom) and their families for their selfless participation. It is your energy and enthusiasm that facilitates and promotes advancements in technical areas that benefit all of society. It is also my pleasure to thank the many people and organizations that make the Awards Banquet possible. First, the companies that have sponsored tonight’s Banquet - their generous support is greatly appreciated. In addition, we thank the many nominators, endorsers, and volunteers who have taken time from their busy schedules to support the awards efforts, especially the Awards Nominating Committee who select and champion the Awardees, and the Awards Banquet Committee which has been working for the last six months planning and implementing tonight's event. I would like to call your attention to two important events for the Long Island Section.