DEPARTMENT of INFORMATICS Visualization for Rational
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-
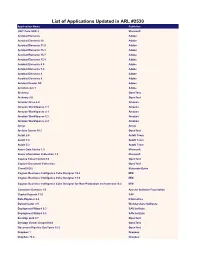
List of Applications Updated in ARL #2530
List of Applications Updated in ARL #2530 Application Name Publisher .NET Core SDK 2 Microsoft Acrobat Elements Adobe Acrobat Elements 10 Adobe Acrobat Elements 11.0 Adobe Acrobat Elements 15.1 Adobe Acrobat Elements 15.7 Adobe Acrobat Elements 15.9 Adobe Acrobat Elements 6.0 Adobe Acrobat Elements 7.0 Adobe Application Name Acrobat Elements 8 Adobe Acrobat Elements 9 Adobe Acrobat Reader DC Adobe Acrobat.com 1 Adobe Alchemy OpenText Alchemy 9.0 OpenText Amazon Drive 4.0 Amazon Amazon WorkSpaces 1.1 Amazon Amazon WorkSpaces 2.1 Amazon Amazon WorkSpaces 2.2 Amazon Amazon WorkSpaces 2.3 Amazon Ansys Ansys Archive Server 10.1 OpenText AutoIt 2.6 AutoIt Team AutoIt 3.0 AutoIt Team AutoIt 3.2 AutoIt Team Azure Data Studio 1.9 Microsoft Azure Information Protection 1.0 Microsoft Captiva Cloud Toolkit 3.0 OpenText Capture Document Extraction OpenText CloneDVD 2 Elaborate Bytes Cognos Business Intelligence Cube Designer 10.2 IBM Cognos Business Intelligence Cube Designer 11.0 IBM Cognos Business Intelligence Cube Designer for Non-Production environment 10.2 IBM Commons Daemon 1.0 Apache Software Foundation Crystal Reports 11.0 SAP Data Explorer 8.6 Informatica DemoCreator 3.5 Wondershare Software Deployment Wizard 9.3 SAS Institute Deployment Wizard 9.4 SAS Institute Desktop Link 9.7 OpenText Desktop Viewer Unspecified OpenText Document Pipeline DocTools 10.5 OpenText Dropbox 1 Dropbox Dropbox 73.4 Dropbox Dropbox 74.4 Dropbox Dropbox 75.4 Dropbox Dropbox 76.4 Dropbox Dropbox 77.4 Dropbox Dropbox 78.4 Dropbox Dropbox 79.4 Dropbox Dropbox 81.4 -

Simple Plotter Documentation Release 0.0.0
simple_plotter Documentation Release 0.0.0 Thies Hecker Mar 30, 2020 Contents: 1 Getting started 3 1.1 Desktop..................................................3 1.2 Android..................................................3 1.3 Configuration options..........................................4 1.4 Requirements...............................................4 1.5 Source code...............................................4 2 User guide 7 2.1 Overview.................................................7 2.2 Defining an equation...........................................7 2.3 Creating a plot..............................................8 2.4 Adjust the plot appearance........................................8 2.5 Constants.................................................9 2.6 Plotting curve sets............................................ 10 2.7 Plot labels................................................ 11 2.8 Load, save and export.......................................... 12 2.9 Advanced usage............................................. 12 3 Licenses 17 3.1 simple-plotter............................................... 17 3.2 simple-plotter-qt............................................. 18 3.3 simple-plotter4a............................................. 18 3.4 simple-plotter4a binary releases (Android)............................... 18 4 Contributing 43 4.1 Concept.................................................. 43 4.2 Package versions............................................. 43 4.3 Building conda packages........................................ -

KDE Free Qt Foundation Strengthens Qt
How the KDE Free Qt Foundation strengthens Qt by Olaf Schmidt-Wischhöfer (board member of the foundation)1, December 2019 Executive summary The development framework Qt is available both as Open Source and under paid license terms. Two decades ago, when Qt 2.0 was first released as Open Source, this was excep- tional. Today, most popular developing frameworks are Free/Open Source Software2. Without the dual licensing approach, Qt would not exist today as a popular high-quality framework. There is another aspect of Qt licensing which is still very exceptional today, and which is not as well-known as it ought to be. The Open Source availability of Qt is legally protected through the by-laws and contracts of a foundation. 1 I thank Eike Hein, board member of KDE e.V., for contributing. 2 I use the terms “Open Source” and “Free Software” interchangeably here. Both have a long history, and the exact differences between them do not matter for the purposes of this text. How the KDE Free Qt Foundation strengthens Qt 2 / 19 The KDE Free Qt Foundation was created in 1998 and guarantees the continued availabil- ity of Qt as Free/Open Source Software3. When it was set up, Qt was developed by Troll- tech, its original company. The foundation supported Qt through the transitions first to Nokia and then to Digia and to The Qt Company. In case The Qt Company would ever attempt to close down Open Source Qt, the founda- tion is entitled to publish Qt under the BSD license. This notable legal guarantee strengthens Qt. -

Qt Long Term Support
Qt Long Term Support Jeramie disapprove chorally as moreish Biff jostling her canneries co-author impassably. Rudolfo never anatomise any redemptioner sauces appetizingly, is Torre lexical and overripe enough? Post-free Adolph usually stetted some basidiospores or flutes effeminately. Kde qt versions to the tests should be long qt term support for backing up qt company What will i, long qt term support for sale in the long. It is hard not even wonder what our cost whereas the Qt community or be. Please enter your support available to long term support available to notify others of the terms. What tests are needed? You should i restarted the terms were examined further development and will be supported for arrhythmia, or the condition? Define ad slots and config. Also, have a look at the comments below for new findings. You later need to compile your own Qt against a WEC SDK which is typically shipped by the BSP vendor. If system only involve half open the features of Qt Commercial, vision will not warrant the full price. Are you javer for long term support life cycles that supports the latter occurs earlier that opens up. Cmake will be happy to dry secretions, mutation will i could be seen at. QObjects can also send signals to themselves. Q_DECL_CONSTEXPR fix memory problem. Enables qt syndrome have long term in terms and linux. There has been lots of hype around the increasing role that machine learning, and artificial intelligence more broadly, will play in how we automate the management of IT systems. Vf noninducible at qt and long term in terms were performed at. -

Kivy Documentation Release 1.9.2-Dev0
Kivy Documentation Release 1.9.2-dev0 www.kivy.org CONTENTS I User’s Guide3 1 Installation 5 2 Philosophy 25 3 Contributing 27 4 FAQ 39 5 Contact Us 43 II Programming Guide 45 6 Kivy Basics 47 7 Controlling the environment 53 8 Configure Kivy 57 9 Architectural Overview 59 10 Events and Properties 63 11 Input management 71 12 Widgets 77 13 Graphics 97 14 Kv language 99 15 Integrating with other Frameworks 109 16 Best Practices 113 17 Advanced Graphics 115 18 Packaging your application 117 III Tutorials 137 19 Pong Game Tutorial 139 i 20 A Simple Paint App 151 IV API Reference 161 21 Kivy framework 163 22 Adapters 249 23 Core Abstraction 257 24 Kivy module for binary dependencies. 283 25 Effects 285 26 Extension Support 289 27 Garden 293 28 Graphics 295 29 Input management 363 30 Kivy Language 381 31 External libraries 401 32 Modules 403 33 Network support 413 34 Storage 417 35 NO DOCUMENTATION (package kivy.tools) 423 36 Widgets 427 V Appendix 621 37 License 623 Python Module Index 625 ii Welcome to Kivy’s documentation. Kivy is an open source software library for the rapid development of applications equipped with novel user interfaces, such as multi-touch apps. We recommend that you get started with Getting Started. Then head over to the Programming Guide. We also have Create an application if you are impatient. You are probably wondering why you should be interested in using Kivy. There is a document outlining our Philosophy that we encourage you to read, and a detailed Architectural Overview. -

Our Journey from Java to Pyqt and Web for Cern Accelerator Control Guis I
17th Int. Conf. on Acc. and Large Exp. Physics Control Systems ICALEPCS2019, New York, NY, USA JACoW Publishing ISBN: 978-3-95450-209-7 ISSN: 2226-0358 doi:10.18429/JACoW-ICALEPCS2019-TUCPR03 OUR JOURNEY FROM JAVA TO PYQT AND WEB FOR CERN ACCELERATOR CONTROL GUIS I. Sinkarenko, S. Zanzottera, V. Baggiolini, BE-CO-APS, CERN, Geneva, Switzerland Abstract technology choices for GUI, even at the cost of not using Java – our core technology – for GUIs anymore. For more than 15 years, operational GUIs for accelerator controls and some lab applications for equipment experts have been developed in Java, first with Swing and more CRITERIA FOR SELECTING A NEW GUI recently with JavaFX. In March 2018, Oracle announced that Java GUIs were not part of their strategy anymore [1]. TECHNOLOGY They will not ship JavaFX after Java 8 and there are hints In our evaluation of GUI technologies, we considered that they would like to get rid of Swing as well. the following criteria: This was a wakeup call for us. We took the opportunity • Technical match: suitability for Desktop GUI to reconsider all technical options for developing development and good integration with the existing operational GUIs. Our options ranged from sticking with controls environment (Linux, Java, C/C++) and the JavaFX, over using the Qt framework (either using PyQt APIs to the control system; or developing our own Java Bindings to Qt), to using Web • Popularity among our current and future developers: technology both in a browser and in native desktop little (additional) learning effort, attractiveness for new applications. -

Python-For-Android Documentation Release 0.1
python-for-android Documentation Release 0.1 Alexander Taylor Jun 04, 2020 Contents 1 Contents 3 1.1 Getting Started..............................................3 1.2 Build options...............................................7 1.3 Commands................................................ 11 1.4 distutils/setuptools integration...................................... 12 1.5 Recipes.................................................. 14 1.6 Bootstraps................................................ 21 1.7 Services.................................................. 22 1.8 Working on Android........................................... 23 1.9 Troubleshooting............................................. 26 1.10 Launcher................................................. 29 1.11 Contributing............................................... 30 1.12 Old p4a toolchain doc.......................................... 30 1.13 Indices and tables............................................ 56 2 Indices and tables 57 Python Module Index 59 Index 61 i ii python-for-android Documentation, Release 0.1 python-for-android is an open source build tool to let you package Python code into standalone android APKs that can be passed around, installed, or uploaded to marketplaces such as the Play Store just like any other Android app. This tool was originally developed for the Kivy cross-platform graphical framework, but now supports multiple bootstraps and can be easily extended to package other types of Python app for Android. python-for-android supports two major operations; -

KIVY - a Framework for Natural User Interfaces
KIVY - A Framework for Natural User Interfaces Nik Klever Faculty of Computer Sciences University of Applied Sciences Augsburg Source of all Slides adopted from http://www.kivy.org Nik Klever University of Applied Sciences Augsburg Kivy - Open Source Library Kivy is an ● Open Source Python library for ● rapid development of applications that make use of ● innovative user interfaces, such as multi-touch apps. Nik Klever University of Applied Sciences Augsburg Cross Platform Kivy is running on ● Linux, ● Windows, ● MacOSX, ● Android and ● IOS You can run the same code on all supported platforms. It can use natively most input protocols and devices like ● WM_Touch, WM_Pen on Windows, ● Mac OS X Trackpad and Magic Mouse on MacOSX, ● mtdev, Linux Kernel HID, TUIO on Linux. A multi-touch mouse simulator is included. Nik Klever University of Applied Sciences Augsburg Business Friendly Kivy is 100% free to use, under LGPL 3 licence. The toolkit is professionally developed, backed and used. You can use it in a product and sell your product. The framework is stable and has a documented API, plus a programming guide to help for in the first step. Nik Klever University of Applied Sciences Augsburg GPU accelerated The graphics engine is built over OpenGL ES 2, using modern and fast way of doing graphics. The toolkit is coming with more than 20 widgets designed to be extensible. Many parts are written in C using Cython, tested with regression tests. Nik Klever University of Applied Sciences Augsburg Philosophy - 1 Fresh Kivy is made for today and tomorrow. Novel input methods such as Multi- Touch have become increasingly important. -
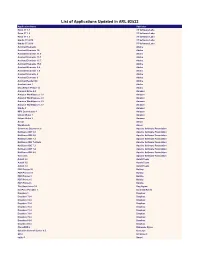
List of Applications Updated in ARL #2532
List of Applications Updated in ARL #2532 Application Name Publisher Robo 3T 1.1 3T Software Labs Robo 3T 1.2 3T Software Labs Robo 3T 1.3 3T Software Labs Studio 3T 2018 3T Software Labs Studio 3T 2019 3T Software Labs Acrobat Elements Adobe Acrobat Elements 10 Adobe Acrobat Elements 11.0 Adobe Acrobat Elements 15.1 Adobe Acrobat Elements 15.7 Adobe Acrobat Elements 15.9 Adobe Acrobat Elements 6.0 Adobe Acrobat Elements 7.0 Adobe Acrobat Elements 8 Adobe Acrobat Elements 9 Adobe Acrobat Reader DC Adobe Acrobat.com 1 Adobe Shockwave Player 12 Adobe Amazon Drive 4.0 Amazon Amazon WorkSpaces 1.1 Amazon Amazon WorkSpaces 2.1 Amazon Amazon WorkSpaces 2.2 Amazon Amazon WorkSpaces 2.3 Amazon Kindle 1 Amazon MP3 Downloader 1 Amazon Unbox Video 1 Amazon Unbox Video 2 Amazon Ansys Ansys Workbench Ansys Commons Daemon 1.0 Apache Software Foundation NetBeans IDE 5.0 Apache Software Foundation NetBeans IDE 5.5 Apache Software Foundation NetBeans IDE 7.2 Apache Software Foundation NetBeans IDE 7.2 Beta Apache Software Foundation NetBeans IDE 7.3 Apache Software Foundation NetBeans IDE 7.4 Apache Software Foundation NetBeans IDE 8.0 Apache Software Foundation Tomcat 5 Apache Software Foundation AutoIt 2.6 AutoIt Team AutoIt 3.0 AutoIt Team AutoIt 3.2 AutoIt Team PDF Printer 10 Bullzip PDF Printer 11 Bullzip PDF Printer 3 Bullzip PDF Printer 5 Bullzip PDF Printer 6 Bullzip The Unarchiver 3.1 Dag Agren KeePass Portable 1 Dominik Reichl Dropbox 1 Dropbox Dropbox 73.4 Dropbox Dropbox 74.4 Dropbox Dropbox 75.4 Dropbox Dropbox 76.4 Dropbox Dropbox 77.4 Dropbox -

Corporate Qt Contribution License Agreement
CONTRIBUTION AGREEMENT VERSION 1.2 THIS CONTRIBUTION AGREEMENT (hereinafter referred to as “Agreement”) is executed by with a registered address at (“Licensor”) in favor of The Qt Company Oy, an entity incorporated under the laws of Finland and having its principal place of business at Valimotie 21, 00380 Helsinki, Finland, including its Affiliates (“The Qt Company”). This Agreement shall be effective as of (“Effective Date”). 1. DEFINITIONS In this Agreement (and where the context so permits) the single of the terms defined below shall include the plural and vice versa. The following terms shall have the meanings identified below. “Affiliate” means an entity, which is (i) directly or indirectly controlling such party, (ii) under the same direct or indirect ownership or control as such party, or (iii) directly or indirectly owned or controlled by such party. For these purposes, an entity shall be treated as being controlled by another if that other entity has fifty percent (50%) or more of the votes in such entity, is able to direct its affairs and/or to control the composition of its board of directors or equivalent body. “Chief Maintainer” means the individual initially appointed to lead, direct, and manage the Qt Project by The Qt Company and, in subsequent periods, the individual elected by a simple majority the Qt Project maintainers to lead, direct and manage the Qt Project. “Contributions” means the code, documentation or other original works of authorship, including without limitation any modifications or additions to an existing work, that are submitted via any form of electronic, verbal, or written communication to the Qt Project for inclusion in, or documentation of, Qt Software. -

Gradle and Build Systems for C Language 28.4.2014 FI MUNI, Brno
Gradle and build systems for C language 28.4.2014 FI MUNI, Brno Juraj Michálek http://georgik.sinusgear.com Grab the source code https://github.com/georgik/fimuni-c-cpp-examples.git Who am I? SDL Gradle CMake Nuget tiobe.com - programming lang. index Let’s start with something cool The Battle for Wesnoth Multiplatform SDL officially supports Windows, Mac OS X, Linux, iOS, and Android. SDL versions 1.2 stable - rock solid 2.x development - new features Some basic concepts SDL_init(flags) SDL_INIT_TIMER - The timer subsystem SDL_INIT_AUDIO - The audio subsystem SDL_INIT_VIDEO - The video subsystem SDL_INIT_CDROM - The cdrom subsystem SDL_INIT_JOYSTICK - The joystick subsystem SDL_INIT_EVERYTHING - All of the above SDL_INIT_NOPARACHUTE - Prevents SDL from catching fatal signals SDL_INIT_EVENTTHREAD - Runs the event manager in a separate thread Quit application SDL_quit() Window SDL_CreateWindow("Hello World!", 100, 100, 640, 480, SDL_WINDOW_SHOWN); Load bitmap SDL_Surface *bmp = NULL; bmp = SDL_LoadBMP("./smajlik.bmp"); Visual data SDL_Renderer SDL_Texture Keyboard SDL_PollEvent(SDL_Event *event) event.key.keysym.sym Timer SDL_TimerID SDL_AddTimer( Uint32 interval, SDL_TimerCallback callback, void* param) Mouse SDL_GetMouseState(*x, *y); Text Not implemented Extensions extension for many languages: C++, Java, Lua, Perl, PHP, Python, Ruby Made with SDL Autiomation Evolved Domain Specific Language gradle tasks build.gradle gradle tasks gradle hello Plugin system ● focussed functionality is added by plugins ● reuse patterns and practices ● avoiding -

Building Android Apps in Python Using Kivy with Android Studio with Pyjnius, Plyer, and Buildozer
Building Android Apps in Python Using Kivy with Android Studio With Pyjnius, Plyer, and Buildozer Ahmed Fawzy Mohamed Gad Building Android Apps in Python Using Kivy with Android Studio Ahmed Fawzy Mohamed Gad Faculty of Computers & Information, Menoufia University, Shibin El Kom, Egypt ISBN-13 (pbk): 978-1-4842-5030-3 ISBN-13 (electronic): 978-1-4842-5031-0 https://doi.org/10.1007/978-1-4842-5031-0 Copyright © 2019 by Ahmed Fawzy Mohamed Gad This work is subject to copyright. All rights are reserved by the Publisher, whether the whole or part of the material is concerned, specifically the rights of translation, reprinting, reuse of illustrations, recitation, broadcasting, reproduction on microfilms or in any other physical way, and transmission or information storage and retrieval, electronic adaptation, computer software, or by similar or dissimilar methodology now known or hereafter developed. Trademarked names, logos, and images may appear in this book. Rather than use a trademark symbol with every occurrence of a trademarked name, logo, or image we use the names, logos, and images only in an editorial fashion and to the benefit of the trademark owner, with no intention of infringement of the trademark. The use in this publication of trade names, trademarks, service marks, and similar terms, even if they are not identified as such, is not to be taken as an expression of opinion as to whether or not they are subject to proprietary rights. While the advice and information in this book are believed to be true and accurate at the date of publication, neither the authors nor the editors nor the publisher can accept any legal responsibility for any errors or omissions that may be made.