DOCSLIB.ORG

Exploring the Einstein Problem

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Exploring the Einstein Problem Exploring The Einstein Problem Thesis submitted at the University of Leicester in partial fulllment of the requirements for the degree of Master of Mathematics by Zoe C. Allwood Department of Mathematics University of Leicester May 2014 Contents Declaration iii Abstract iv Introduction 1 1 Describing the Tile 4 1.1 Lines and Flags . 4 1.2 Lines and Coloured Diagonals . 5 1.3 Other Representations . 6 2 Proof of Aperiodicity 7 3 The Substitution Tiling 12 3.1 Simplifying the Tile Set . 13 3.2 The Substitution . 17 3.3 The Substitution on the Simplied Tile Sets . 19 3.4 Amalgamation . 22 3.5 Proof of Aperiodicity . 22 4 A Better Einstein 23 4.1 Unconnected Tile . 23 4.2 3D Tile . 24 4.2.1 Construction . 24 4.2.2 Issues . 26 i 4.3 Schmitt, Conway and Danzer Tile . 26 4.4 Issues . 27 4.4.1 Height . 27 4.4.2 Tile Orientation . 27 4.4.3 Aperiodic Layers . 28 4.5 Danzer Implementation Attempt . 28 4.5.1 Rotation of 2π .............................. 28 3 4.5.2 Irrational Rotation . 30 4.6 Aperiodic Stack . 31 4.6.1 Thue Morse exploration . 32 4.6.2 General explanation . 33 4.6.3 Two dimensional exploration . 33 5 Conclusions 34 5.1 Socolar and Taylor Tile . 34 5.2 Einsteins and Dimension . 35 Bibliography 36 ii Declaration All sentences or passages quoted in this project dissertation from other people's work have been specically acknowledged by clear cross referencing to author, work and page(s). I understand that failure to do this amounts to plagiarism and will be considered grounds for failure in this module and the degree examination as a whole. Name: Signed: Date: iii Abstract The Einstein problem is an attempt to nd an aperiodic prototile set that consists of a single tile. After some basic denitions and a more detailed explanation of the problem we look at the tile that ts this denition the best, created by Socolar and Taylor. The rst chapter is an explanation of two of the ways this tile can be dened. The second chapter is a proof of the non-periodicity of all tilings created by this prototile based on the hierarchical structure of them. The third chapter is looking at the tile set as a substitution tiling creating an easier way to make tilings in a computer and also show all tilings are non-periodic more easily. The fourth shows other constructions of the tile, including a three dimensional one, and explorations into trying to improve the tile by trying to remove some of the issues with the tile in its current forms. iv Introduction The Einstein problem is very simple to explain but very hard to nd a solution to, like Fermat's last theorem. It is the problem of whether a single aperiodic prototile exists. The name comes from a play on words as Einstein in German can be translated roughly as "one stone". As Fermat hinted in the margin of a book regarding his problem, there is quite possibly a simple and rigorous way to nd solutions to this type of problem, but at the moment we are working with trial and error. If a solution, or groups of solutions, can be found it will have a profound eect on the understanding of certain crystalline structures which are aperiodic and can be understood better in terms of these tilings. The current solutions to this problem are not complete; there are many ways that the current tiles can be improved. In this work we explore a tile that is a good Einstein, found by Socolar and Taylor [2, 3], show it is aperiodic in a way that is complementary to the original proof. We will then discuss the issues with it and try and look at ways to improve it. Basic Notions These are some denitions that we are going to be using throughout this work. The general details of tilings are explored thoroughly by Grunbaum and Shephard[1]. n Denition 0.1. A tiling is a subdivision of R into pieces called tiles. These tiles only n intersect at their boundaries and their union is R . Tiling is most commonly done in 2 dimensions, tiling the plane, but an equivalent is possible in any dimension. In one dimension line segments can be used to `tile' the line. A tile can be given a label, letting you distinguish between tiles of the same shape. 1 Thinking of these labels as colour would dierentiate between a simple square tiling and a checkerboard tiling. Denition 0.2. Prototiles are the set of tiles that make up a tiling ignoring position. For the checkerboard tiling the prototile set would be a black square and a white square. Another way to think of a tiling is as a collection of translates, translations and/ or rotations, of a prototile set so that each translate only intersects with others at its n boundary and the union of the collection is R . Denition 0.3. Matching rules are the guidelines for how tiles are allowed to be placed in regards to each other. The rule that tiles must meet full edge to full edge is an example of a matching rule that is generally applied to tilings. The two ways to force a matching rule are by markings on the tile or by the shape of the tile. The relationship between markings on the tiles can be dened in any way that creates the tilings wanted and most of these relationships can be dened instead using shape, though this can create very complicated tiles when dealing with complex matching rules. Denition 0.4. A patch is a nite section of a tiling. If you have a nite set of protiles and a set of matching rules, for example having to meet full edge to full edge, then you can only create a nite number of patches. This number generally increases very quickly as you increase the possible size of the patch but at any nite size there are only a nite number of possible patches. This is called having nite local complexity. Denition 0.5. A tiling is called periodic if the whole tiling is created by regular repetition of a nite patch of the tiling. This means the placement of one version of this patch can completely dene the position of all other tiles in the tiling. It is called non-periodic if this is not the case. Using the example of the checkerboard tiling, you can determine what colour of tile will be a certain distance from a known tile in the tiling without having to work out all the tiles 2 in between because of the regularity. If you took a standard square tiling and randomly split each square into two triangles by adding in one of the diagonals there is no way to deduce which diagonal was added using already known ones as it is completely random. This created tiling is therefore non-periodic. Though there is not any regularly repeating pattern, because the tiling has nite local complexity there are only nite patches of every size. Because of this there will be innitely many copies of every patch, but they will not appear with any regularity. There are many prototiles sets that can produce some periodic tilings and some non- periodic tilings as well. If you add the same diagonal to every square, instead of a random choice, you would get a periodic tiling from the same triangular prototile as the non-periodic tiling already dened. Denition 0.6. A prototile set is called aperiodic if every tiling it can create is non- periodic. These are the prototile sets we are interested in. A famous example of these are the Penrose tilings but with these there are always at least two dierent tiles in the prototile set, so they are not an Einstein. Using the denitions above an Einstein is an aperiodic prototile set consisting of a single tile. This means that using a single tile you can cover the entire plane without ever having a regularly repeating pattern. Because of the nite local complexity every patch of the tiling will repeat but this will never happen regularly. The tile we will describe below ts this denition. 3 Chapter 1 Describing the Tile Though Socolar and Taylor have dened a single tile, created from a hexagon, it can be useful to describe it in dierent ways. The matching rules cannot be dened simply by shape, unless the tile becomes unconnected or you use a substitution with multiple tiles. Also you need to use the fundamentally dierent mirror image to successfully tile the plane; you do not need this if you make the tile three dimensional. All these interpretations are explained in this work. Any pictures that do not have a reference were created for this work. 1.1 Lines and Flags The prototile is a hexagon with markings to enforce local matching rules. There are black lines, two short lines around the top and bottom vertexes and a long one connecting the two remaining edges o center. The distance between the end of the short black line and nearby top or bottom vertex must be the same distance as the end of the long black line and the top vertex of the edge it is touching. At every vertex there is a ag. The top and bottom ags always point the same way and the other four ags point away from the long black line. As the long black line is o-center of the edges it touches this prototile is chiral, its mirror image is fundamentally dierent to itself.
Load more

Recommended publications
  • ICES REPORT 14-22 Characterization, Enumeration and Construction Of
    ICES REPORT 14-22 August 2014 Characterization, Enumeration and Construction of Almost-regular Polyhedra by Muhibur Rasheed and Chandrajit Bajaj The Institute for Computational Engineering and Sciences The University of Texas at Austin Austin, Texas 78712 Reference: Muhibur Rasheed and Chandrajit Bajaj, "Characterization, Enumeration and Construction of Almost-regular Polyhedra," ICES REPORT 14-22, The Institute for Computational Engineering and Sciences, The University of Texas at Austin, August 2014. Characterization, Enumeration and Construction of Almost-regular Polyhedra Muhibur Rasheed and Chandrajit Bajaj Center for Computational Visualization Institute of Computational Engineering and Sciences The University of Texas at Austin Austin, Texas, USA Abstract The symmetries and properties of the 5 known regular polyhedra are well studied. These polyhedra have the highest order of 3D symmetries, making them exceptionally attractive tem- plates for (self)-assembly using minimal types of building blocks, from nanocages and virus capsids to large scale constructions like glass domes. However, the 5 polyhedra only represent a small number of possible spherical layouts which can serve as templates for symmetric assembly. In this paper, we formalize the notion of symmetric assembly, specifically for the case when only one type of building block is used, and characterize the properties of the corresponding layouts. We show that such layouts can be generated by extending the 5 regular polyhedra in a sym- metry preserving way. The resulting family remains isotoxal and isohedral, but not isogonal; hence creating a new class outside of the well-studied regular, semi-regular and quasi-regular classes and their duals Catalan solids and Johnson solids. We also show that this new family, dubbed almost-regular polyhedra, can be parameterized using only two variables and constructed efficiently.
    [Show full text]
  • Fundamental Principles Governing the Patterning of Polyhedra
    FUNDAMENTAL PRINCIPLES GOVERNING THE PATTERNING OF POLYHEDRA B.G. Thomas and M.A. Hann School of Design, University of Leeds, Leeds LS2 9JT, UK. [email protected] ABSTRACT: This paper is concerned with the regular patterning (or tiling) of the five regular polyhedra (known as the Platonic solids). The symmetries of the seventeen classes of regularly repeating patterns are considered, and those pattern classes that are capable of tiling each solid are identified. Based largely on considering the symmetry characteristics of both the pattern and the solid, a first step is made towards generating a series of rules governing the regular tiling of three-dimensional objects. Key words: symmetry, tilings, polyhedra 1. INTRODUCTION A polyhedron has been defined by Coxeter as “a finite, connected set of plane polygons, such that every side of each polygon belongs also to just one other polygon, with the provision that the polygons surrounding each vertex form a single circuit” (Coxeter, 1948, p.4). The polygons that join to form polyhedra are called faces, 1 these faces meet at edges, and edges come together at vertices. The polyhedron forms a single closed surface, dissecting space into two regions, the interior, which is finite, and the exterior that is infinite (Coxeter, 1948, p.5). The regularity of polyhedra involves regular faces, equally surrounded vertices and equal solid angles (Coxeter, 1948, p.16). Under these conditions, there are nine regular polyhedra, five being the convex Platonic solids and four being the concave Kepler-Poinsot solids. The term regular polyhedron is often used to refer only to the Platonic solids (Cromwell, 1997, p.53).
    [Show full text]
  • Computability and Tiling Problems
    Computability and Tiling Problems Mark Richard Carney University of Leeds School of Mathematics Submitted in accordance with the requirements for the degree of Doctor of Philosophy October 2019 Intellectual Property Statement The candidate confirms that the work submitted is his own and that appropriate credit has been given where reference has been made to the work of others. This copy has been supplied on the understanding that it is copy- right material and that no quotation from the thesis may be pub- lished without proper acknowledgement. The right of Mark Richard Carney to be identified as Author of this work has been asserted by him in accordance with the Copyright, Designs and Patents Act 1988. c October 2019 The University of Leeds and Mark Richard Carney. i Abstract In this thesis we will present and discuss various results pertaining to tiling problems and mathematical logic, specifically computability theory. We focus on Wang prototiles, as defined in [32]. We begin by studying Domino Problems, and do not restrict ourselves to the usual problems concerning finite sets of prototiles. We first consider two domino problems: whether a given set of prototiles S has total planar tilings, which we denote T ILE, or whether it has infinite connected but not necessarily total tilings, W T ILE (short for ‘weakly tile’). We show that both T ILE ≡m ILL ≡m W T ILE, and thereby both T ILE 1 and W T ILE are Σ1-complete. We also show that the opposite problems, :T ILE and SNT (short for ‘Strongly Not Tile’) are such that :T ILE ≡m W ELL ≡m 1 SNT and so both :T ILE and SNT are both Π1-complete.
    [Show full text]
  • REPLICATING TESSELLATIONS* ANDREW Vincet Abstract
    SIAM J. DISC. MATH. () 1993 Society for Industrial and Applied Mathematics Vol. 6, No. 3, pp. 501-521, August 1993 014 REPLICATING TESSELLATIONS* ANDREW VINCEt Abstract. A theory of replicating tessellation of R is developed that simultaneously generalizes radix representation of integers and hexagonal addressing in computer science. The tiling aggregates tesselate Eu- clidean space so that the (m + 1)st aggregate is, in turn, tiled by translates of the ruth aggregate, for each m in exactly the same way. This induces a discrete hierarchical addressing systsem on R'. Necessary and sufficient conditions for the existence of replicating tessellations are given, and an efficient algorithm is provided to de- termine whether or not a replicating tessellation is induced. It is shown that the generalized balanced ternary is replicating in all dimensions. Each replicating tessellation yields an associated self-replicating tiling with the following properties: (1) a single tile T tesselates R periodically and (2) there is a linear map A, such that A(T) is tiled by translates of T. The boundary of T is often a fractal curve. Key words, tiling, self-replicating, radix representation AMS(MOS) subject classifications. 52C22, 52C07, 05B45, 11A63 1. Introduction. The standard set notation X + Y {z + y z E X, y E Y} will be used. For a set T c Rn denote by Tx z + T the translate of T to point z. Throughout this paper, A denotes an n-dimensional lattice in l'. A set T tiles a set R by translation by lattice A if R [-JxsA T and the intersection of the interiors of distinct tiles T and Tu is empty.
    [Show full text]
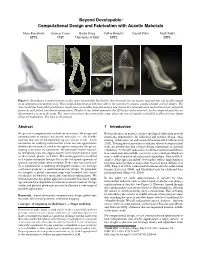
  • Omputational Design and Fabrication with Auxetic Materials
    Beyond Developable: Computational Design and Fabrication with Auxetic Materials Mina Konakovic´ Keenan Crane Bailin Deng Sofien Bouaziz Daniel Piker Mark Pauly EPFL CMU University of Hull EPFL EPFL Figure 1: Introducing a regular pattern of slits turns inextensible, but flexible sheet material into an auxetic material that can locally expand in an approximately uniform way. This modified deformation behavior allows the material to assume complex double-curved shapes. The shoe model has been fabricated from a single piece of metallic material using a new interactive rationalization method based on conformal geometry and global, non-linear optimization. Thanks to our global approach, the 2D layout of the material can be computed such that no discontinuities occur at the seam. The center zoom shows the region of the seam, where one row of triangles is doubled to allow for easy gluing along the boundaries. The base is 3D printed. Abstract 1 Introduction We present a computational method for interactive 3D design and Recent advances in material science and digital fabrication provide rationalization of surfaces via auxetic materials, i.e., flat flexible promising opportunities for industrial and product design, engi- material that can stretch uniformly up to a certain extent. A key neering, architecture, art and science [Caneparo 2014; Gibson et al. motivation for studying such material is that one can approximate 2015]. To bring these innovations to fruition, effective computational doubly-curved surfaces (such as the sphere) using only flat pieces, tools are needed that link creative design exploration to material making it attractive for fabrication. We physically realize surfaces realization. A versatile approach is to abstract material and fabrica- by introducing cuts into approximately inextensible material such tion constraints into suitable geometric representations which are as sheet metal, plastic, or leather.
    [Show full text]
  • Contractions of Octagonal Tilings with Rhombic Tiles. Frédéric Chavanon, Eric Remila
    View metadata, citation and similar papers at core.ac.uk brought to you by CORE provided by Archive Ouverte en Sciences de l'Information et de la Communication Contractions of octagonal tilings with rhombic tiles. Frédéric Chavanon, Eric Remila To cite this version: Frédéric Chavanon, Eric Remila. Contractions of octagonal tilings with rhombic tiles.. [Research Report] LIP RR-2003-44, Laboratoire de l’informatique du parallélisme. 2003, 2+12p. hal-02101891 HAL Id: hal-02101891 https://hal-lara.archives-ouvertes.fr/hal-02101891 Submitted on 17 Apr 2019 HAL is a multi-disciplinary open access L’archive ouverte pluridisciplinaire HAL, est archive for the deposit and dissemination of sci- destinée au dépôt et à la diffusion de documents entific research documents, whether they are pub- scientifiques de niveau recherche, publiés ou non, lished or not. The documents may come from émanant des établissements d’enseignement et de teaching and research institutions in France or recherche français ou étrangers, des laboratoires abroad, or from public or private research centers. publics ou privés. Laboratoire de l’Informatique du Parallelisme´ Ecole´ Normale Sup´erieure de Lyon Unit´e Mixte de Recherche CNRS-INRIA-ENS LYON no 5668 Contractions of octagonal tilings with rhombic tiles Fr´ed´eric Chavanon, Eric R´emila Septembre 2003 Research Report No 2003-44 Ecole´ Normale Superieure´ de Lyon, 46 All´ee d’Italie, 69364 Lyon Cedex 07, France T´el´ephone : +33(0)4.72.72.80.37 Fax : +33(0)4.72.72.80.80 Adresseelectronique ´ : [email protected] Contractions of octagonal tilings with rhombic tiles Fr´ed´eric Chavanon, Eric R´emila Septembre 2003 Abstract We prove that the space of rhombic tilings of a fixed octagon can be given a canonical order structure.
    [Show full text]
  • Five-Vertex Archimedean Surface Tessellation by Lanthanide-Directed Molecular Self-Assembly
    Five-vertex Archimedean surface tessellation by lanthanide-directed molecular self-assembly David Écijaa,1, José I. Urgela, Anthoula C. Papageorgioua, Sushobhan Joshia, Willi Auwärtera, Ari P. Seitsonenb, Svetlana Klyatskayac, Mario Rubenc,d, Sybille Fischera, Saranyan Vijayaraghavana, Joachim Reicherta, and Johannes V. Bartha,1 aPhysik Department E20, Technische Universität München, D-85478 Garching, Germany; bPhysikalisch-Chemisches Institut, Universität Zürich, CH-8057 Zürich, Switzerland; cInstitute of Nanotechnology, Karlsruhe Institute of Technology, D-76344 Eggenstein-Leopoldshafen, Germany; and dInstitut de Physique et Chimie des Matériaux de Strasbourg (IPCMS), CNRS-Université de Strasbourg, F-67034 Strasbourg, France Edited by Kenneth N. Raymond, University of California, Berkeley, CA, and approved March 8, 2013 (received for review December 28, 2012) The tessellation of the Euclidean plane by regular polygons has by five interfering laser beams, conceived to specifically address been contemplated since ancient times and presents intriguing the surface tiling problem, yielded a distorted, 2D Archimedean- aspects embracing mathematics, art, and crystallography. Sig- like architecture (24). nificant efforts were devoted to engineer specific 2D interfacial In the last decade, the tools of supramolecular chemistry on tessellations at the molecular level, but periodic patterns with surfaces have provided new ways to engineer a diversity of sur- distinct five-vertex motifs remained elusive. Here, we report a face-confined molecular architectures, mainly exploiting molecular direct scanning tunneling microscopy investigation on the cerium- recognition of functional organic species or the metal-directed directed assembly of linear polyphenyl molecular linkers with assembly of molecular linkers (5). Self-assembly protocols have terminal carbonitrile groups on a smooth Ag(111) noble-metal sur- been developed to achieve regular surface tessellations, includ- face.
    [Show full text]
  • Grade 6 Math Circles Tessellations Tiling the Plane
    Faculty of Mathematics Centre for Education in Waterloo, Ontario N2L 3G1 Mathematics and Computing Grade 6 Math Circles October 13/14, 2015 Tessellations Tiling the Plane Do the following activity on a piece of graph paper. Build a pattern that you can repeat all over the page. Your pattern should use one, two, or three different `tiles' but no more than that. It will need to cover the page with no holes or overlapping shapes. Think of this exercises as if you were using tiles to create a pattern for your kitchen counter or a floor. Your pattern does not have to fill the page with straight edges; it can be a pattern with bumpy edges that does not fit the page perfectly. The only rule here is that we have no holes or overlapping between our tiles. Here are two examples, one a square tiling and another that we will call the up-down arrow tiling: Another word for tiling is tessellation. After you have created a tessellation, study it: did you use a weird shape or shapes? Or is your tiling simple and only uses straight lines and 1 polygons? Recall that a polygon is a many sided shape, with each side being a straight line. For example, triangles, trapezoids, and tetragons (quadrilaterals) are all polygons but circles or any shapes with curved sides are not polygons. As polygons grow more sides or become more irregular, you may find it difficult to use them as tiles. When given the previous activity, many will come up with the following tessellations.
    [Show full text]
  • Generating Apparently-Random Colour Patterns
    Computational Aesthetics in Graphics, Visualization, and Imaging (2012) D. Cunningham and D. House (Editors) Random Discrete Colour Sampling Henrik Lieng Christian Richardt Neil A. Dodgson Generating apparently-randomUniversity of Cambridge colour patterns Used with permission of the authors Figure 1: We present an algorithm that distributes colours randomly using a human-centric definition of randomness. Left: Colours distributed using Matlab’s random-number generator. Middle: Result of our algorithm. Notice that our algorithm does not produce any distinctive patterns. Right: An image similar to one of Damien Hirst’s spot paintings. Abstract Apparently-random distributions of colours in a discrete setting have been used by many artists and craftsmen in the past century. Manual colourisation is a tedious and difficult process. Automatic colourisation, on the other hand, tends not to not look ‘random’ to a human, as randomly-generated clusters and patterns stimulate human perception and break the appearance of randomness. We propose an algorithm that minimises these apparent patterns, making the distribution of colours look as if they have been distributed randomly by a human. We show that our approach is superior to current solutions, especially for small numbers of colours. Our algorithm is easily extendible to non-regular patterns in any coordinate system. Categories and Subject Descriptors (according to ACM CCS): I.3.8 [Computer Graphics]: Applications; I.3.m [Com- puter Graphics]: Miscellaneous—Visual Arts; J.5 [Arts and Humanities]: Fine Arts. 1. Introduction Random colour sampling in the spatially discrete space was used in the early twentieth-century by numerous artists such as Jean Arp, Sophie Tauber and Vilmos Huszár.
    [Show full text]
  • Convex Polytopes and Tilings with Few Flag Orbits
    Convex Polytopes and Tilings with Few Flag Orbits by Nicholas Matteo B.A. in Mathematics, Miami University M.A. in Mathematics, Miami University A dissertation submitted to The Faculty of the College of Science of Northeastern University in partial fulfillment of the requirements for the degree of Doctor of Philosophy April 14, 2015 Dissertation directed by Egon Schulte Professor of Mathematics Abstract of Dissertation The amount of symmetry possessed by a convex polytope, or a tiling by convex polytopes, is reflected by the number of orbits of its flags under the action of the Euclidean isometries preserving the polytope. The convex polytopes with only one flag orbit have been classified since the work of Schläfli in the 19th century. In this dissertation, convex polytopes with up to three flag orbits are classified. Two-orbit convex polytopes exist only in two or three dimensions, and the only ones whose combinatorial automorphism group is also two-orbit are the cuboctahedron, the icosidodecahedron, the rhombic dodecahedron, and the rhombic triacontahedron. Two-orbit face-to-face tilings by convex polytopes exist on E1, E2, and E3; the only ones which are also combinatorially two-orbit are the trihexagonal plane tiling, the rhombille plane tiling, the tetrahedral-octahedral honeycomb, and the rhombic dodecahedral honeycomb. Moreover, any combinatorially two-orbit convex polytope or tiling is isomorphic to one on the above list. Three-orbit convex polytopes exist in two through eight dimensions. There are infinitely many in three dimensions, including prisms over regular polygons, truncated Platonic solids, and their dual bipyramids and Kleetopes. There are infinitely many in four dimensions, comprising the rectified regular 4-polytopes, the p; p-duoprisms, the bitruncated 4-simplex, the bitruncated 24-cell, and their duals.
    [Show full text]
  • Ordered Equilibrium Structures of Patchy Particle Systems
    Dissertation Ordered Equilibrium Structures of Patchy Particle Systems ausgef¨uhrt zum Zwecke der Erlangung des akademischen Grades eines Doktors der technischen Wissenschaften unter der Leitung von Ao. Univ. Prof. Dr. Gerhard Kahl Institut f¨ur Theoretische Physik Technische Universit¨at Wien eingereicht an der Technischen Universit¨at Wien Fakult¨at f¨ur Physik von Dipl.-Ing. G¨unther Doppelbauer Matrikelnummer 0225956 Franzensgasse 10/6, 1050 Wien Wien, im Juli 2012 G¨unther Doppelbauer Kurzfassung Systeme der weichen Materie, die typischerweise aus mesoskopischen Teilchen in einem L¨osungsmittel aus mikroskopischen Teilchen bestehen, k¨onnen bei niedrigen Temperaturen im festen Aggregatzustand in einer Vielzahl von geordneten Struk- turen auftreten. Die Vorhersage dieser Strukturen bei bekannten Teilchenwechsel- wirkungen und unter vorgegebenen thermodynamischen Bedingungen wurde in den letzten Jahrzehnten als eines der großen ungel¨osten Probleme der Physik der kondensierten (weichen) Materie angesehen. In dieser Arbeit wird ein Ver- fahren vorgestellt, das die geordneten Phasen dieser Systeme vorhersagt; dieses beruht auf heuristischen Optimierungsmethoden, wie etwa evolution¨aren Algorith- men. Um die thermodynamisch stabile geordnete Teilchenkonfiguration an einem bestimmten Zustandspunkt zu finden, wird das entsprechende thermodynamische Potential minimiert und die dem globalen Minimum entsprechende Phase identifi- ziert. Diese Technik wird auf Modellsysteme f¨ur sogenannte kolloidale “Patchy Particles” angewandt. Die “Patches” sind dabei als begrenzte Regionen mit abweichen- den physikalischen oder chemischen Eigenschaften auf der Oberfl¨ache kolloidaler Teilchen definiert. “Patchy Particles” weisen, zus¨atzlich zur isotropen Hart- kugelabstoßung der Kolloide, sowohl abstoßende als auch anziehende anisotrope Wechselwirkungen zwischen den “Patches” auf. Durch neue Synthetisierungs- methoden k¨onnen solche Teilchen mit maßgeschneiderten Eigenschaften erzeugt werden.
    [Show full text]
  • Eindhoven University of Technology MASTER Lateral Stiffness Of
    Eindhoven University of Technology MASTER Lateral stiffness of hexagrid structures de Meijer, J.H.M. Award date: 2012 Link to publication Disclaimer This document contains a student thesis (bachelor's or master's), as authored by a student at Eindhoven University of Technology. Student theses are made available in the TU/e repository upon obtaining the required degree. The grade received is not published on the document as presented in the repository. The required complexity or quality of research of student theses may vary by program, and the required minimum study period may vary in duration. General rights Copyright and moral rights for the publications made accessible in the public portal are retained by the authors and/or other copyright owners and it is a condition of accessing publications that users recognise and abide by the legal requirements associated with these rights. • Users may download and print one copy of any publication from the public portal for the purpose of private study or research. • You may not further distribute the material or use it for any profit-making activity or commercial gain ‘Lateral Stiffness of Hexagrid Structures’ - Master’s thesis – - Main report – - A 2012.03 – - O 2012.03 – J.H.M. de Meijer 0590897 July, 2012 Graduation committee: Prof. ir. H.H. Snijder (supervisor) ir. A.P.H.W. Habraken dr.ir. H. Hofmeyer Eindhoven University of Technology Department of the Built Environment Structural Design Preface This research forms the main part of my graduation thesis on the lateral stiffness of hexagrids. It explores the opportunities of a structural stability system that has been researched insufficiently.
    [Show full text]