DOCSLIB.ORG

Spherical Euclidean Distance Embedding of a Graph

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Spherical Euclidean Distance Embedding of a Graph Spherical Euclidean Distance Embedding of a Graph Hou-Duo Qi University of Southampton Presented at Isaac Newton Institute Polynomial Optimization August 9, 2013 Spherical Embedding Problem The Problem: Given n points in <m, place them on Sr(c; R) { the sphere in <r with the center at c and the radius R so that some Euclidean distance proper- ties among the n points are \best" kept. The most interesting cases are when some or all of the parame- ters (d; c; R) are unknown. n n 0. Notation: Pre-distance matrix, Sh , and S+ Pre-distance matrix (dissimilarity matrix): I D is symmetric I Dii = 0 (zero diagonals) I Dij ≥ 0 (non-negativities) n n n S , S+, and Sh (Hollow subspace): n I S := fall n × n symmetric matricesg ; n n I Sh := fX 2 S : Xii = 0 8 ig n n I S+ := the set of all PSD matrices in S : 1. Squared Euclidean Distance Matrix (EDM) A n × n matrix D is a (squared) Euclidean Distance r Matrix (EDM) if there exist points p1;:::; pn in < such that 2 Dij = kpi − pjk 8 i; j: ? Squared pairwise distances are used. ? <r is called embedding space and r ≤ n − 1. ? The smallest such r is the embedding dimension of D. 2. The Cone of EDMs I The set of all n × n EDMs is a closed convex cone. 3. Characterization of EDM: Schoenberg (1935), Young and Householder (1938) I Schoenberg in (Ann. Math. 1935), and (independently) Young and Householder in (Psychometrika, 1938). n D is EDM () D 2 Sh and − (JDJ) 0; where 1 J = I − eeT =n or (J = I − ): n I Furthermore, let 1 B = − JDJ; 2 and B has the following decomposition: B = PP T ; with P 2 <n×r: Let pi = P (i; :), we have 2 Dij = kpi − pjk : 3. Characterization of EDM: Schoenberg (1935), Young and Householder (1938) Remarks (R1) The Schoenberg-Young-Householder characterization has two steps: The first step is to versify whether a given matrix is EDM. The second step is the embedding step by computing a spectral decomposition. (R2) It has become a major method for data dimension reduction { the classical Multidimensional Scaling (cMDS). (R3) The matrix JDJ has zero as its eigenvalue. Therefore, the Slater condition is never satisfied for the constraint: −JDJ 0: 4. Partial Distances among 50 Sensors 5. Algorithm: Isomap I Many methods are available I Euclidean distance matrix completion (Laurent (1997), Wolkowicz, Anjos et. al from 1999 {) I Y. Ye and his co-authors on Semi-Definite Programming (SDP) Relaxations (from 2004 {) I Kim et. al on Sparse Full SDP (2009, 2012) I Mor´eand Wu (DGSOL package, Argonne National Laboratory, 1999). I Several more packages (e.g., PENNON). I Isomap by Tenenbaum, Silva, and Langford (Science 2000). I Regard the problem as a network (graph) problem. Length of the edge is the distance (not necessarily accurate) I Replace the missing distances by the shortest path distances in the graph. I Use the Schoenberg-Young-Householder method to recover the locations of the nodes. 4 Points Embedding 4 Points Embedding by Isomap Computing Nearest EDM I Given a pre-distance matrix D, find a true EDM matrix Y that is the nearest to D: min kY − Dk2 s.t. Y is EDM rank(JYJ) ≤ r (embedding dimension constraint) I By the Schoenberg-Young-Householder characterization, we have n Y is EDM () Y 2 Sh ; −JYJ 0: I We have a convex quadratic SDP. 4 Points Embedding by EMBED (Q. and Yuan 2012) 6. Another Characterization of EDM I Hayden and Wells (SIMAX, 1990) and Gaffke and Mathar (Metrika,1989): n n D is EDM () D 2 Sh \ (−K+); where n n n T ?o K+ := A 2 S : x Ax ≥ 0; x 2 e : n Note: K+ is a closed convex cone. n I K+ as projected spectrahedra: n T K+ = A j (A; t ≥ 0) such that A − tee 0 n I K+ as set-copositive cone. I Conic Formulation of the nearest EDM (Q. and Yuan 2012): 2 n n min kY −Dk s.t. Y 2 Sh \(−K+); and rank(JXJ) ≤ r: 7. Dealing with Spherical Constraints I We now want to place n points on a sphere: kxik = R: I We assume the center to be the (n + 1)th point xn+1 so that 2 2 kxi − xn+1k = R ; 8 i = 1;:::; 2: I The formulation of optimization problems with spherical constraints takes the following form: min = max f(Y ) n n+1 s.t. Y 2 Sh \ (−K+ ) rank(JXJ) ≤ r Y1(n+1) = Yi(n+1); i = 2; : : : ; n: I When there are no rank constraint, the problem is often convex (many such problems from geometric embedding of graphs). 8. Smallest Hypersphere Representation of a Grpah I Def. Let G = (V; E) be a graph with jV j = n.A unit-distance representation of g is a system of n vectors (p1;:::; pn) in a Euclidean space such that kpi − pjk = 1 8 (i; j) 2 E: I Def. If furthermore, kpik = kpjk 8 i; j 2 V the system is called a hypersphere representation of G. Unit-distance realization of Petersen graph on plane 8. Smallest Hypersphere Representation of a Graph I Finding the smallest radius of a hypersphere representation (Lov´asz('09), Silva and Tuncel ('10)) th(G) := min t s.t. diag(X) = te Xii − 2Xij + Xjj = 1; 8 (i; j) 2 E n X 2 S+; t 2 <: I It is known 1 2th(G) + = 1: #(G) I EDM formulation: min Y1(n+1) n n+1 s.t. Y 2 Sh \ (−K+ ) Yij = 1 8 (i; j) 2 E Y1(n+1) = Yi(n+1); i = 2; : : : ; n: 9. Lov´asz-thetaFunction I Def. An orthonormal representation of G is a system fp1;:::; png of unit vectors in a Euclidean distance space such that hpi; pji = 0 8 (i; j) 62 E: Theorem 5, Lov´asz('79): Let (p1;:::; pn) range over all orthonormal representations of G and d over all unit vectors. Then n X 2 #(G) = max (hd; pii) : i=1 I SDP formulation: #(G) = max hJ; Xi s.t. hI;Xi = 1 Xij = 0; 8 (i; j) 2 E X 0: From Projection to Euclidean Distance I We have 2 2 2 kd − pik = kdk + kpik − 2hd; pii = 2 − 2hd; pii: Hence 1 2 (hd; p i)2 = 1 − kd − p k2 : i 4 i 0 I Under the condition (part of Schrijver's # function): hd; pii ≥ 0; we have 1 2 max (hd; p i)2 () min kd − p k2 i 4 i I This leads to the following EDM problem 1 Pn 22 p(G) := min 4 i=1 kd − pik s.t. kpik = 1; kdk = 1; hpi; pji = 0 8 (i; j) 2 E: A Quantity that may be interesting I For a given graph, define the quantity q(G) such that p pp(G) + pq(G) = n: I Let SOL(G) denote the solution set of the SDP of # function. Define b(#) τ := p ; # n where Pn p b(#) := max i=1 Bii s.t. B 2 SOL(G): I For vertex-transitive graphs τ# = 1: Bound that measures Distortion I Define p r# := n=#(G) and 1 p t := r − (r − 1)2 + 2r(1 − τ): # τ I Define the distortion constant d# by d# := t#τ# I Claim (Bound of Distortion): 2 d##(G) ≤ q(G) ≤ #(G): I Remark: d# hard to calculate. But for vertex-transitive graphs, we have d# = 1: Is Triangle Inequality `2 Metric? I One can add triangle inequalities to SDP to strengthen # function: Xik + Xjk ≤ Xij + Xkk (i; j; k 2 V ): I Let X 0 admit the Gram representation: X = P T P: Therefore, 2 kpi − pkk = Xii + Xkk − 2Xik: 2 I ` -metric: 2 2 2 kpi − pkk + kpj − pkk ≥ kpi − pkk which implies 1 X + X ≤ X + (X + X ): ik jk ik 2 kk jj A Wild Guess I The close τ# to 1, the less room that adding cut (triangle) inequalities can strengthen #(G). I Example is vertex-transitive graphs. I We can measure this by computing the ratio: #(G) q(G) Both are convex problems..
Load more

Recommended publications
  • Euclidean Space - Wikipedia, the Free Encyclopedia Page 1 of 5
    Euclidean space - Wikipedia, the free encyclopedia Page 1 of 5 Euclidean space From Wikipedia, the free encyclopedia In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions. The term “Euclidean” distinguishes these spaces from the curved spaces of non-Euclidean geometry and Einstein's general theory of relativity, and is named for the Greek mathematician Euclid of Alexandria. Classical Greek geometry defined the Euclidean plane and Euclidean three-dimensional space using certain postulates, while the other properties of these spaces were deduced as theorems. In modern mathematics, it is more common to define Euclidean space using Cartesian coordinates and the ideas of analytic geometry. This approach brings the tools of algebra and calculus to bear on questions of geometry, and Every point in three-dimensional has the advantage that it generalizes easily to Euclidean Euclidean space is determined by three spaces of more than three dimensions. coordinates. From the modern viewpoint, there is essentially only one Euclidean space of each dimension. In dimension one this is the real line; in dimension two it is the Cartesian plane; and in higher dimensions it is the real coordinate space with three or more real number coordinates. Thus a point in Euclidean space is a tuple of real numbers, and distances are defined using the Euclidean distance formula. Mathematicians often denote the n-dimensional Euclidean space by , or sometimes if they wish to emphasize its Euclidean nature. Euclidean spaces have finite dimension. Contents 1 Intuitive overview 2 Real coordinate space 3 Euclidean structure 4 Topology of Euclidean space 5 Generalizations 6 See also 7 References Intuitive overview One way to think of the Euclidean plane is as a set of points satisfying certain relationships, expressible in terms of distance and angle.
    [Show full text]
  • Distance Between Points on the Earth's Surface
    Distance between Points on the Earth's Surface Abstract During a casual conversation with one of my students, he asked me how one could go about computing the distance between two points on the surface of the Earth, in terms of their respective latitudes and longitudes. This is an interesting exercise in spherical coordinates, and relates to the so-called haversine. The calculation of the distance be- tween two points on the surface of the Spherical coordinates Earth proceeds in two stages: (1) to z compute the \straight-line" Euclidean x=Rcosθcos φ distance these two points (obtained by y=Rcosθsin φ R burrowing through the Earth), and (2) z=Rsinθ to convert this distance to one mea- θ y sured along the surface of the Earth. φ Figure 1 depicts the spherical coor- dinates we shall use.1 We orient this coordinate system so that x Figure 1: Spherical Coordinates (i) The origin is at the Earth's center; (ii) The x-axis passes through the Prime Meridian (0◦ longitude); (iii) The xy-plane contains the Earth's equator (and so the positive z-axis will pass through the North Pole) Note that the angle θ is the measurement of lattitude, and the angle φ is the measurement of longitude, where 0 ≤ φ < 360◦, and −90◦ ≤ θ ≤ 90◦. Negative values of θ correspond to points in the Southern Hemisphere, and positive values of θ correspond to points in the Northern Hemisphere. When one uses spherical coordinates it is typical for the radial distance R to vary; however, in our discussion we may fix it to be the average radius of the Earth: R ≈ 6; 378 km: 1What is depicted are not the usual spherical coordinates, as the angle θ is usually measure from the \zenith", or z-axis.
    [Show full text]
  • LAB 9.1 Taxicab Versus Euclidean Distance
    ([email protected] LAB 9.1 Name(s) Taxicab Versus Euclidean Distance Equipment: Geoboard, graph or dot paper If you can travel only horizontally or vertically (like a taxicab in a city where all streets run North-South and East-West), the distance you have to travel to get from the origin to the point (2, 3) is 5.This is called the taxicab distance between (0, 0) and (2, 3). If, on the other hand, you can go from the origin to (2, 3) in a straight line, the distance you travel is called the Euclidean distance, or just the distance. Finding taxicab distance: Taxicab distance can be measured between any two points, whether on a street or not. For example, the taxicab distance from (1.2, 3.4) to (9.9, 9.9) is the sum of 8.7 (the horizontal component) and 6.5 (the vertical component), for a total of 15.2. 1. What is the taxicab distance from (2, 3) to the following points? a. (7, 9) b. (–3, 8) c. (2, –1) d. (6, 5.4) e. (–1.24, 3) f. (–1.24, 5.4) Finding Euclidean distance: There are various ways to calculate Euclidean distance. Here is one method that is based on the sides and areas of squares. Since the area of the square at right is y 13 (why?), the side of the square—and therefore the Euclidean distance from, say, the origin to the point (2,3)—must be ͙ෆ13,or approximately 3.606 units. 3 x 2 Geometry Labs Section 9 Distance and Square Root 121 © 1999 Henri Picciotto, www.MathEducationPage.org ([email protected] LAB 9.1 Name(s) Taxicab Versus Euclidean Distance (continued) 2.
    [Show full text]
  • SCALAR PRODUCTS, NORMS and METRIC SPACES 1. Definitions Below, “Real Vector Space” Means a Vector Space V Whose Field Of
    SCALAR PRODUCTS, NORMS AND METRIC SPACES 1. Definitions Below, \real vector space" means a vector space V whose field of scalars is R, the real numbers. The main example for MATH 411 is V = Rn. Also, keep in mind that \0" is a many splendored symbol, with meaning depending on context. It could for example mean the number zero, or the zero vector in a vector space. Definition 1.1. A scalar product is a function which associates to each pair of vectors x; y from a real vector space V a real number, < x; y >, such that the following hold for all x; y; z in V and α in R: (1) < x; x > ≥ 0, and < x; x > = 0 if and only if x = 0. (2) < x; y > = < y; x >. (3) < x + y; z > = < x; z > + < y; z >. (4) < αx; y > = α < x; y >. n The dot product is defined for vectors in R as x · y = x1y1 + ··· + xnyn. The dot product is an example of a scalar product (and this is the only scalar product we will need in MATH 411). Definition 1.2. A norm on a real vector space V is a function which associates to every vector x in V a real number, jjxjj, such that the following hold for every x in V and every α in R: (1) jjxjj ≥ 0, and jjxjj = 0 if and only if x = 0. (2) jjαxjj = jαjjjxjj. (3) (Triangle Inequality for norm) jjx + yjj ≤ jjxjj + jjyjj. p The standard Euclidean norm on Rn is defined by jjxjj = x · x.
    [Show full text]
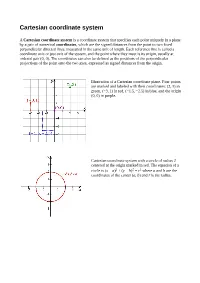
  • Cartesian Coordinate System
    Cartesian coordinate system A Cartesian coordinate system is a coordinate system that specifies each point uniquely in a plane by a pair of numerical coordinates, which are the signed distances from the point to two fixed perpendicular directed lines, measured in the same unit of length. Each reference line is called a coordinate axis or just axis of the system, and the point where they meet is its origin, usually at ordered pair (0, 0). The coordinates can also be defined as the positions of the perpendicular projections of the point onto the two axes, expressed as signed distances from the origin. Illustration of a Cartesian coordinate plane. Four points are marked and labeled with their coordinates: (2, 3) in green, (−3, 1) in red, (−1.5, −2.5) in blue, and the origin (0, 0) in purple. Cartesian coordinate system with a circle of radius 2 centered at the origin marked in red. The equation of a circle is (x − a)2 + (y − b)2 = r2 where a and b are the coordinates of the center (a, b) and r is the radius. Distance between two points The Euclidean distance between two points of the plane with Cartesian coordinates and is This is the Cartesian version of Pythagoras's theorem. In three-dimensional space, the distance between points and is which can be obtained by two consecutive applications of Pythagoras' theorem. To draw a circle using Cartesian coordinate system 1. Considering two points x and y on the x-axis and y-axis which meet at (x,y), this produces a right angle triangle with base of length x and height y.
    [Show full text]
  • On Euclidean Distance Matrices and Spherical Configurations
    On Euclidean Distance Matrices and Spherical Configurations. A.Y. Alfakih Dept of Math and Statistics University of Windsor DIMACS Workshop on Optimization in Distance Geometry June 26-28, 2019 Outline I Survey of EDMs: I Characterizations. I Properties. I Classes of EDMs: Spherical and Nonspherical. I EDM Inverse Eigenvalue Problem. I Spherical Configurations I Yielding and Nonyielding Entries. I Unit Spherical EDMs which differ in 1 entry. I Two-Distance Sets. I The dimension of the affine span of the generating points of an EDM D is called the embedding dimension of D. I An EDM D is spherical if its generating points lie on a hypersphere. Otherwise, it is nonspherical. Definition 1 n I An n × n matrix D is an EDM if there exist points p ;:::; p in some Euclidean space such that: i j 2 dij = jjp − p jj for all i; j = 1;:::; n: I An EDM D is spherical if its generating points lie on a hypersphere. Otherwise, it is nonspherical. Definition 1 n I An n × n matrix D is an EDM if there exist points p ;:::; p in some Euclidean space such that: i j 2 dij = jjp − p jj for all i; j = 1;:::; n: I The dimension of the affine span of the generating points of an EDM D is called the embedding dimension of D. Definition 1 n I An n × n matrix D is an EDM if there exist points p ;:::; p in some Euclidean space such that: i j 2 dij = jjp − p jj for all i; j = 1;:::; n: I The dimension of the affine span of the generating points of an EDM D is called the embedding dimension of D.
    [Show full text]
  • 1 Euclidean Vector Spaces
    1 Euclidean Vector Spaces 1.1 Euclidean n-space In this chapter we will generalize the ¯ndings from last chapters for a space with n dimensions, called n-space. De¯nition 1 If n 2 Nnf0g, then an ordered n-tuple is a sequence of n numbers in R:(a1; a2; : : : ; an). The set of all ordered n-tuples is called n-space and is denoted by Rn. The elements in Rn can be perceived as points or vectors, similar to what we have done in 2- and 3-space. (a1; a2; a3) was used to indicate the components of a vector or the coordinates of a point. De¯nition 2 n Two vectors u = (u1; u2; : : : ; un) and v = (v1; v2; : : : ; vn) in R are called equal if u1 = v1; u2 = v2; : : : ; un = vn The sum u + v is de¯ned by u + v = (u1 + v1; u2 + v2; : : : un + vn) If k 2 R the scalar multiple of u is de¯ned by ku = (ku1; ku2; : : : ; kun) These operations are called the standard operations in Rn. De¯nition 3 The zero vector 0 in Rn is de¯ned by 0 = (0; 0;:::; 0) n For u = (u1; u2; : : : ; un) 2 R the negative of u is de¯ned by ¡u = (¡u1; ¡u2;:::; ¡un) The di®erence between two vectors u; v 2 Rn is de¯ned by u ¡ v = u + (¡v) Theorem 1 If u; v and w in Rn and k; l 2 R, then (a) u + v = v + u (b) (u + v) + w = u + (v + w) 1 (c) u + 0 = u (d) u + (¡u) = 0 (e) k(lu) = (kl)u (f) k(u + v) = ku + kv (g) (k + l)u = ku + lu (h) 1u) = u This theorem permits us to manipulate equations without writing them in component form.
    [Show full text]
  • Math 135 Notes Parallel Postulate .Pdf
    Euclidean verses Non Euclidean Geometries Euclidean Geometry Euclid of Alexandria was born around 325 BC. Most believe that he was a student of Plato. Euclid introduced the idea of an axiomatic geometry when he presented his 13 chapter book titled The Elements of Geometry. The Elements he introduced were simply fundamental geometric principles called axioms and postulates. The most notable are Euclid’s five postulates which are stated in the next passage. 1) Any two points can determine a straight line. 2) Any finite straight line can be extended in a straight line. 3) A circle can be determined from any center and any radius. 4) All right angles are equal. 5) If two straight lines in a plane are crossed by a transversal, and sum the interior angle of the same side of the transversal is less than two right angles, then the two lines extended will intersect. According to Euclid, the rest of geometry could be deduced from these five postulates. Euclid’s fifth postulate, often referred to as the Parallel Postulate, is the basis for what are called Euclidean Geometries or geometries where parallel lines exist. There is an alternate version to Euclid fifth postulate which is usually stated as “Given a line and a point not on the line, there is one and only one line that passed through the given point that is parallel to the given line. This is a short version of the Parallel Postulate called Fairplay’s Axiom which is named after the British math teacher who proposed to replace the axiom in all of the schools textbooks.
    [Show full text]
  • Course Notes Geometric Algebra for Computer Graphics∗ SIGGRAPH 2019
    Course notes Geometric Algebra for Computer Graphics∗ SIGGRAPH 2019 Charles G. Gunn, Ph. D.y ∗Permission to make digital or hard copies of part or all of this work for personal or classroom use is granted without fee provided that copies are not made or distributed for profit or commercial advantage and that copies bear this notice and the full citation on the first page. Copyrights for third-party components of this work must be honored. For all other uses, contact the Owner/Author. Copyright is held by the owner/author(s). SIGGRAPH '19 Courses, July 28 - August 01, 2019, Los Angeles, CA, USA ACM 978-1-4503-6307-5/19/07. 10.1145/3305366.3328099 yAuthor's address: Raum+Gegenraum, Brieselanger Weg 1, 14612 Falkensee, Germany, Email: [email protected] 1 Contents 1 The question 4 2 Wish list for doing geometry 4 3 Structure of these notes 5 4 Immersive introduction to geometric algebra 6 4.1 Familiar components in a new setting . .6 4.2 Example 1: Working with lines and points in 3D . .7 4.3 Example 2: A 3D Kaleidoscope . .8 4.4 Example 3: A continuous 3D screw motion . .9 5 Mathematical foundations 11 5.1 Historical overview . 11 5.2 Vector spaces . 11 5.3 Normed vector spaces . 12 5.4 Sylvester signature theorem . 12 5.5 Euclidean space En ........................... 13 5.6 The tensor algebra of a vector space . 13 5.7 Exterior algebra of a vector space . 14 5.8 The dual exterior algebra . 15 5.9 Projective space of a vector space .
    [Show full text]
  • Polar Coordinate Routing for Multiple Paths in Wireless Networks
    Polar Coordinate Routing for Multiple Paths in Wireless Networks Maulik Desai Nicholas Maxemchuk Department of Electrical Engineering Columbia University maulik,nick @ee.columbia.edu { } Abstract—We propose Polar Coordinate Routing (PCR) to terms of path separation, average number of hops etc. There is create multiple paths between a source and a destination in some work in the wireless networking domain that shows how wireless networks. Our scheme creates paths that are circular to forward messages on a trajectory, however this solution has segments of different radii connecting a source and a destina- tion. We propose a non euclidean distance metric that allows not been tested for multiple paths. Moreover, it does not offer messages to travel along− these paths. Using PCR it is possible to a good solution to circumnavigate obstacles and the areas with maintain a known separation among the paths, which reduces the low node density. interference between the nodes belonging to two separate routes. In this paper we present a simple way to form circular Our extensive simulations show that while PCR achieves a known arcs between a source destination pair. We present a simple separation between the routes, it does so with a small increase in non Euclidean distance metric using which messages can overall hop count. Moreover, we demonstrate that the variances − of average separation and hop count are lower for the paths be forwarded through the nodes that are closest to these created using PCR compared to existing schemes, indicating a arcs. We also show that the arcs maintain a high level of more reliable system.
    [Show full text]
  • Euclidean Distance Matrix Trick
    Euclidean Distance Matrix Trick Samuel Albanie Visual Geometry Group University of Oxford [email protected] June, 2019 Abstract This is a short note discussing the cost of computing Euclidean Distance Matrices. 1 Computing Euclidean Distance Matrices d Suppose we have a collection of vectors fxi 2 R : i 2 f1; : : : ; ngg and we want to compute the n × n matrix, D, of all pairwise distances between them. We first consider the case where each element in the matrix represents the squared Euclidean distance (see Sec.3 for the non-square case) 1, a calculation that frequently arises in machine learning and computer vision. The distance matrix is defined as follows: 2 Dij = jjxi − xjjj2 (1) or equivalently, T 2 T 2 Dij = (xi − xj) (xi − xj) = jjxijj2 − 2xi xj + jjxjjj2 (2) There is a popular “trick” for computing Euclidean Distance Matrices (although it’s perhaps more of an observation than a trick). The observation is that it is generally preferable to compute the second expression, rather than the first2. Writing X 2 Rd×n for the matrix formed by stacking the collection of vectors as columns, we can compute Eqn.1 by creating two views of the matrix with shapes of d × n × 1 and d × 1 × n respectively. In libraries such as numpy,PyTorch,Tensorflow etc. these operations are essentially free because they simply modify the meta-data associated with the matrix, rather than the underlying elements in memory. We then compute the difference between these reshaped matrices, square all resulting elements and sum along the zeroth dimension to produce D, as shown in Algorithm1.
    [Show full text]
  • Dimensionality Reduction Via Euclidean Distance Embeddings
    School of Computer Science and Communication CVAP - Computational Vision and Active Perception Dimensionality Reduction via Euclidean Distance Embeddings Marin Šarić, Carl Henrik Ek and Danica Kragić TRITA-CSC-CV 2011:2 CVAP320 Marin Sari´c,Carlˇ Henrik Ek and Danica Kragi´c Dimensionality Reduction via Euclidean Distance Embeddings Report number: TRITA-CSC-CV 2011:2 CVAP320 Publication date: Jul, 2011 E-mail of author(s): [marins,chek,dani]@csc.kth.se Reports can be ordered from: School of Computer Science and Communication (CSC) Royal Institute of Technology (KTH) SE-100 44 Stockholm SWEDEN telefax: +46 8 790 09 30 http://www.csc.kth.se/ Dimensionality Reduction via Euclidean Distance Embeddings Marin Sari´c,Carlˇ Henrik Ek and Danica Kragi´c Centre for Autonomous Systems Computational Vision and Active Perception Lab School of Computer Science and Communication KTH, Stockholm, Sweden [marins,chek,dani]@csc.kth.se Contents 1 Introduction2 2 The Geometry of Data3 D 2.1 The input space R : the geometry of observed data.............3 2.2 The configuration region M ...........................4 2.3 The use of Euclidean distance in the input space as a measure of dissimilarity5 q 2.4 Distance-isometric output space R .......................6 3 The Sample Space of a Data Matrix7 3.1 Centering a dataset through projections on the equiangular vector.....8 4 Multidimensional scaling - a globally distance isometric embedding 10 4.1 The relationship between the Euclidean distance matrix and the kernel matrix 11 4.1.1 Generalizing to Mercer kernels..................... 13 4.1.2 Generalizing to any metric....................... 13 4.2 Obtaining output coordinates from an EDM.................
    [Show full text]