DOCSLIB.ORG

Success and Failure of Adaptation-Diffusion Algorithms for Consensus in Multi-Agent Networks Gemma Morral, Pascal Bianchi, Gersende Fort

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Success and Failure of Adaptation-Diffusion Algorithms for Consensus in Multi-Agent Networks Gemma Morral, Pascal Bianchi, Gersende Fort Success and Failure of Adaptation-Diffusion Algorithms for Consensus in Multi-Agent Networks Gemma Morral, Pascal Bianchi, Gersende Fort To cite this version: Gemma Morral, Pascal Bianchi, Gersende Fort. Success and Failure of Adaptation-Diffusion Algo- rithms for Consensus in Multi-Agent Networks. 2014. hal-01078466 HAL Id: hal-01078466 https://hal.archives-ouvertes.fr/hal-01078466 Preprint submitted on 29 Oct 2014 HAL is a multi-disciplinary open access L’archive ouverte pluridisciplinaire HAL, est archive for the deposit and dissemination of sci- destinée au dépôt et à la diffusion de documents entific research documents, whether they are pub- scientifiques de niveau recherche, publiés ou non, lished or not. The documents may come from émanant des établissements d’enseignement et de teaching and research institutions in France or recherche français ou étrangers, des laboratoires abroad, or from public or private research centers. publics ou privés. Success and Failure of Adaptation-Diffusion Algorithms for Consensus in Multi-Agent Networks Gemma Morral∗, Pascal Bianchi and Gersende Fort Abstract—This paper investigates the problem of distributed of some other j’s and computes the weighted average: stochastic approximation in multi-agent systems. The algorithm N under study consists of two steps: a local stochastic approxi- ˜ mation step and a diffusion step which drives the network to θn,i = wn(i,j) θn,j , (2) a consensus. The diffusion step uses row-stochastic matrices to Xj=1 weight the network exchanges. As opposed to previous works, where the wn(i,j)’s are scalar non-negative random coeffi- exchange matrices are not supposed to be doubly stochastic, and N may also depend on the past estimate. cients such that j=1 wn(i,j) = 1 for any i. The sequence N We prove that non-doubly stochastic matrices generally in- of random matricesP Wn := [wn(i,j)]i,j=1 represents the fluence the limit points of the algorithm. Nevertheless, the limit time-varying communication network between the nodes. One points are not affected by the choice of the matrices provided that simply set wn(i,j) = 0 whenever nodes i and j are unable to the latter are doubly-stochastic in expectation. This conclusion communicate at time n. The aim of this paper is to investigate legitimates the use of broadcast-like diffusion protocols, which are easier to implement. Next, by means of a central limit theorem, the almost sure (a.s.) convergence of this algorithm as n tends we prove that doubly stochastic protocols perform asymptotically to infinity as well as the convergence rate. Our goal is in as well as centralized algorithms and we quantify the degradation particular to quantify the effect of the sequence of matrices caused by the use of non doubly stochastic matrices. Throughout (Wn)n 1 on the convergence. The algorithm is initialized at the paper, a special emphasis is put on the special case of some arbitrary≥ Rd-valued vectors θ , ,θ . distributed non-convex optimization as an illustration of our 0,1 ··· 0,N results. Application to distributed optimization. The algo- rithm (1)-(2) under study is not new. The idea beyond the algorithm traces back to [5], [6] where a network of processors seeks to optimize some objective function known by all agents I. INTRODUCTION (possibly up to some additive noise). More recently, numerous Distributed stochastic approximation has been recently pro- works extended this kind of algorithm to more involved multi- posed using different cooperative approaches. In the so-called agent scenarios, see [7]–[19] as a non-exhaustive list. In this incremental approach (see for instance [1]–[4]) a message context, one seeks to minimize a sum of local private cost containing an estimate of the quantity of interest iteratively functions fi of the agents: travels all over the network. This paper focuses on another N cooperative approach based on average consensus techniques min fi(θ) , (3) θ Rd where the estimates computed locally by each agent are ∈ Xi=1 combined through the network. where for all i, the function fi is supposed to be unknown Consider a network composed by N agents, or nodes. by any other agent j,j = i. To address this question, it is Agents seek to find a consensus on some global parameter by assumed that 6 means of local observations and peer-to-peer communications. Yn,i = fi(θn 1,i)+ ξn,i (4) The aim of this paper is to analyze the behavior of the follow- −∇ − ing distributed algorithm. Node i (i = 1,...,N) generates a where is the gradient operator and ξn,i represents some d ∇ R -valued stochastic process (θn,i)n 0. At time n, the update random perturbation which possibly occurs when observing ≥ is in two steps: the gradient. In this paper, we handle the case where functions ˜ [Local step] Node i generates a temporary iterate θn,i fi are not necessarily convex. Of course, in that case, there is given by generally no hope to ensure the convergence to a minimizer to (3). Instead, a more realistic objective is to achieve crit- θ˜n,i = θn 1,i + γn Yn,i , (1) − ical points of the objective function i.e., points θ such that where γn is a deterministic positive step size and where the i fi(θ) = 0. d ∇ R -valued random process (Yn,i)n 1 represents the observa- PConvergence to a global minimizer is shown in [20] as- tions made by agent i. ≥ suming convex utility functions and bounded (sub)gradients. [Gossip step] Node i is able to observe the values θ˜n,j The results of [20] are extended in [21] to the stochastic descent case i.e., when the observation of utility functions *This work is supported by DGA (French Armement Procurement Agency), is perturbed by a random noise. More recently, [14] investi- the Institut Mines-Tel´ ecom´ and by the ANR grant ODISSEE of program gated distributed stochastic approximation at large, providing ASTRID (ANR-13-ASTR-0030). stability conditions of the algorithm (1)-(2) while relaxing the G. Morral, P. Bianchi and G. Fort are with LTCI, Tel´ ecom´ Paris- Tech & CNRS, 46 rue Barrault, 75634 Paris Cedex 13, France bounded gradient assumption and including the case of random [firstname].[lastname]@telecom-paristech.fr communication links. In [14], it is also proved under some hypotheses that the estimation error is asymptotically normal: necessarily doubly stochastic. We show that non-doubly the convergence rate and the asymptotic covariance matrix are stochastic matrix have an influence on the asymptotic characterized. An enhanced averaging algorithm a` la Polyak error covariance (even if they are doubly stochastic in is also proposed to recover the optimal convergence rate. average). On the other hand, we prove that when the Doubly and non-doubly stochastic matrices. In most matrix Wn is doubly stochastic for all n, the asymptotic works (see for instance [20]–[22]), the matrices (Wn)n 1 are covariance is identical to the one obtained in a central- T 1 1≥ 1 assumed doubly stochastic, meaning that Wn = Wn = ized setting. where 1 is the N 1 vector whose components are all The paper is organized as follows. Section II is a gentle × equal to one and where T denotes transposition. Although presentation of our results in the special case of distributed 1 1 row-stochasticity (Wn = ) is rather easy to ensure in optimization (see (3)) assuming in addition that sequence T 1 1 practice, column-stochasticity (Wn = ) implies more strin- (Wn) is i.i.d. In Section III we provide the general setting gent restrictions on the communication protocol. For instance, to study almost sure convergence. Almost sure convergence in [23], each one-way transmission from an agent i to another is studied in Section IV. Section V investigates convergence agent j requires at the same time a feedback link from j rates. Conclusions and numerical results complete the paper. to i. As a matter of fact, double stochasticity prevents from Notations: Throughout the paper, the vectors are column using natural broadcast schemes, in which a given node may vectors. The random variables W RN N and Y := transmit its local estimate to all neighbors without expecting n × n (Y T ,...,Y T )T RdN , n 1, are∈ defined on the same any immediate feedback. n,1 n,N measurable space equipped∈ with≥ a probability P; E denotes Remarkably, although generally assumed, double stochastic- the associated expectation. For any n 1, define the σ- ity of the matrices W is in fact not mandatory. A couple of n field F := σ(θ ,W ,...,W ,Y ,...,Y≥) where θ is the works (see e.g. [14], [24]) get rid of the column-stochasticity n 0 1 n 1 n 0 (possibly random) initial point of the algorithm. condition, but at the price of assumptions that may not always It is assumed that for any i 1,...,N, (θn,i)n 0 satisfies the be satisfied in practice. Other works ([17], [25], [26]) manage ≥ update equations (1)-(2); and∈ we set to circumvent the use of feedback links by coupling the gradient descent with the so-called push-sum protocol [27]. T T T θn := (θn,1,...,θn,N ) . The latter however introduces an additional communication of weights in the network in order to keep track of some For any vector x Rℓ, x represents the Euclidean norm of ∈ | | T summary of the past transmissions. In this paper, we address x. IN is the N N identity matrix. J := 11 /N denotes the the following questions: What conditions on the sequence orthogonal projector× onto the linear span of the all-one N 1 × (Wn)n 1 are needed to ensure that Algorithm (1)-(2) drives vector 1, and J := IN J.
Load more

Recommended publications
  • The Geometry of Convex Cones Associated with the Lyapunov Inequality and the Common Lyapunov Function Problem∗
    Electronic Journal of Linear Algebra ISSN 1081-3810 A publication of the International Linear Algebra Society Volume 12, pp. 42-63, March 2005 ELA www.math.technion.ac.il/iic/ela THE GEOMETRY OF CONVEX CONES ASSOCIATED WITH THE LYAPUNOV INEQUALITY AND THE COMMON LYAPUNOV FUNCTION PROBLEM∗ OLIVER MASON† AND ROBERT SHORTEN‡ Abstract. In this paper, the structure of several convex cones that arise in the studyof Lyapunov functions is investigated. In particular, the cones associated with quadratic Lyapunov functions for both linear and non-linear systems are considered, as well as cones that arise in connection with diagonal and linear copositive Lyapunov functions for positive linear systems. In each of these cases, some technical results are presented on the structure of individual cones and it is shown how these insights can lead to new results on the problem of common Lyapunov function existence. Key words. Lyapunov functions and stability, Convex cones, Matrix equations. AMS subject classifications. 37B25, 47L07, 39B42. 1. Introduction and motivation. Recently, there has been considerable inter- est across the mathematics, computer science, and control engineering communities in the analysis and design of so-called hybrid dynamical systems [7,15,19,22,23]. Roughly speaking, a hybrid system is one whose behaviour can be described math- ematically by combining classical differential/difference equations with some logic based switching mechanism or rule. These systems arise in a wide variety of engineer- ing applications with examples occurring in the aircraft, automotive and communi- cations industries. In spite of the attention that hybrid systems have received in the recent past, important aspects of their behaviour are not yet completely understood.
    [Show full text]
  • Arxiv:1909.13402V1 [Math.CA] 30 Sep 2019 Routh-Hurwitz Array [14], Argument Principle [23] and So On
    ON GENERALIZATION OF CLASSICAL HURWITZ STABILITY CRITERIA FOR MATRIX POLYNOMIALS XUZHOU ZHAN AND ALEXANDER DYACHENKO Abstract. In this paper, we associate a class of Hurwitz matrix polynomi- als with Stieltjes positive definite matrix sequences. This connection leads to an extension of two classical criteria of Hurwitz stability for real polynomials to matrix polynomials: tests for Hurwitz stability via positive definiteness of block-Hankel matrices built from matricial Markov parameters and via matricial Stieltjes continued fractions. We obtain further conditions for Hurwitz stability in terms of block-Hankel minors and quasiminors, which may be viewed as a weak version of the total positivity criterion. Keywords: Hurwitz stability, matrix polynomials, total positivity, Markov parameters, Hankel matrices, Stieltjes positive definite sequences, quasiminors 1. Introduction Consider a high-order differential system (n) (n−1) A0y (t) + A1y (t) + ··· + Any(t) = u(t); where A0;:::;An are complex matrices, y(t) is the output vector and u(t) denotes the control input vector. The asymptotic stability of such a system is determined by the Hurwitz stability of its characteristic matrix polynomial n n−1 F (z) = A0z + A1z + ··· + An; or to say, by that all roots of det F (z) lie in the open left half-plane <z < 0. Many algebraic techniques are developed for testing the Hurwitz stability of matrix polynomials, which allow to avoid computing the determinant and zeros: LMI approach [20, 21, 27, 28], the Anderson-Jury Bezoutian [29, 30], matrix Cauchy indices [6], lossless positive real property [4], block Hurwitz matrix [25], extended arXiv:1909.13402v1 [math.CA] 30 Sep 2019 Routh-Hurwitz array [14], argument principle [23] and so on.
    [Show full text]
  • Non-Hurwitz Classical Groups
    London Mathematical Society ISSN 1461–1570 NON-HURWITZ CLASSICAL GROUPS R. VINCENT and A.E. ZALESSKI Abstract In previous work by Di Martino, Tamburini and Zalesski [Comm. Algebra 28 (2000) 5383–5404] it is shown that cer- tain low-dimensional classical groups over finite fields are not Hurwitz. In this paper the list is extended by adding the spe- cial linear and special unitary groups in dimensions 8,9,11,13. We also show that all groups Sp(n, q) are not Hurwitz for q even and n =6, 8, 12, 16. In the range 11 <n<32 many of these groups are shown to be non-Hurwitz. In addition, we observe that PSp(6, 3), P Ω±(8, 3k), P Ω±(10,q), Ω(11, 3k), Ω±(14, 3k), Ω±(16, 7k), Ω(n, 7k) for n =9, 11, 13, PSp(8, 7k) are not Hurwitz. 1. Introduction A finite group H = 1 is called Hurwitz if it is generated by two elements X, Y satisfying the conditions X2 = Y 3 =(XY )7 = 1. A long-standing problem is that of classifying simple Hurwitz groups. The problem has been solved for alternating groups by Conder [4], and for sporadic groups by several authors with the latest result by Wilson [27]. It remains open for groups of Lie type and for classical groups. 3 2 Quite a lot is known. Groups D4(q) for (q, 3)=1, G2(q),G2(q) are Hurwitz with 3 k few exceptions, groups D4(3 ) are not Hurwitz; see Jones [10] and Malle [15, 16].
    [Show full text]
  • Analysis and Control of Linear Time–Varying Systems Exercise 2.3
    Analysis and control of linear time–varying 2 systems Before considering the actual subject matter, i.e., analysis and control design of nonlinear systems, at first linear time-varying systems or LTV systems of the form x˙ A(t)x B(t)u, t t , x(t ) x (2.1a) Æ Å È 0 0 Æ 0 y C(t)x D(t)u, t t (2.1b) Æ Å ¸ 0 with x(t) Rn, u(t) Rm, y(t) Rp and 2 2 2 n n n m p n p m A(t): RÅ R £ , B(t): RÅ R £ , C(t): RÅ R £ , D(t): RÅ R £ t 0 ! t 0 ! t 0 ! t 0 ! are considered. Here RÅ : {t R t t 0} denotes the set of real numbers larger or equal to t0. t 0 Æ 2 j ¸ The motivation behind this sequential approach is that LTV systems on the one hand show certain similarities to linear time–invariant systems but are distinguished by significant differences in their dynamic analysis. In this sense, they — at least to some extend — resemble nonlinear systems. On the other hand, the linearization of a nonlinear system around a solution trajectory t (x¤(t),u¤(t)) 7! yields an LTV system. Hence the subsequently introduced tools can be used for control and observer design at least in a neighborhood of the trajectory (x¤(t),u¤(t)). 2.1 Transition matrix and solution of the state differential equations At first free or autonomous systems x˙ A(t)x, t t , x(t ) x (2.2) Æ È 0 0 Æ 0 are addressed.
    [Show full text]
  • Learning Stable Dynamical Systems Using Contraction Theory
    Learning Stable Dynamical Systems using Contraction Theory eingereichte MASTERARBEIT von cand. ing. Caroline Blocher geb. am 19.08.1990 wohnhaft in: Leonrodstrasse 72 80636 M¨unchen Tel.: 0176 27250499 Lehrstuhl f¨ur STEUERUNGS- und REGELUNGSTECHNIK Technische Universit¨atM¨unchen Univ.-Prof. Dr.-Ing./Univ. Tokio Martin Buss Fachgebiet f¨ur DYNAMISCHE MENSCH-ROBOTER-INTERAKTION f¨ur AUTOMATISIERUNGSTECHNIK Technische Universit¨atM¨unchen Prof. Dongheui Lee, Ph.D. Betreuer: M.Sc. Matteo Saveriano Beginn: 03.08.2015 Zwischenbericht: 25.09.2015 Abgabe: 19.01.2016 In your final hardback copy, replace this page with the signed exercise sheet. Abstract This report discusses the learning of robot motion via non-linear dynamical systems and Gaussian Mixture Models while optimizing the trade-off between global stability and accurate reproduction. Contrary to related work, the approach used in this thesis seeks to guarantee the stability via Contraction Theory. This point of view allows the use of results in robust control theory and switched linear systems for the analysis of the global stability of the dynamical system. Furthermore, a modification of existing approaches to learn a globally stable system and an approach to locally stabilize an already learned system are proposed. Both approaches are based on Contraction Theory and are compared to existing methods. Zusammenfassung Diese Arbeit behandelt das Lernen von stabilen dynamischen Systemen ¨uber eine Gauss’sche Mischverteilung. Im Gegensatz zu bisherigen Arbeiten wird die Sta- bilit¨at des Systems mit Hilfe der Contraction Theory untersucht. Ergebnisse aus der robusten Regulung und der Stabilit¨at von schaltenden Systemen k¨onnen so ¨ubernommen werden. Um die Stabilit¨at des dynamischen Systems zu garantieren und gleichzeitig die Bewegung des gelernten Systems m¨oglichst wenig zu beein- flussen, wird eine Anpassung der bereits bestehenden Methode an die Bewegung vorgeschlagen.
    [Show full text]
  • Generalized Hurwitz Matrices, Generalized Euclidean Algorithm
    Generalized Hurwitz matrices, generalized Euclidean algorithm, and forbidden sectors of the complex plane Olga Holtz∗†, Sergey Khrushchev,‡ and Olga Kushel§ June 23, 2015 Abstract Given a polynomial n n−1 f(x)= a0x + a1x + · · · + an with positive coefficients ak, and a positive integer M ≤ n, we define a(n infinite) generalized Hurwitz matrix HM (f):=(aMj−i)i,j . We prove that the polynomial f(z) does not vanish in the sector π z ∈ C : | arg(z)| < n M o whenever the matrix HM is totally nonnegative. This result generalizes the classical Hurwitz’ Theo- rem on stable polynomials (M = 2), the Aissen-Edrei-Schoenberg-Whitney theorem on polynomials with negative real roots (M = 1), and the Cowling-Thron theorem (M = n). In this connection, we also develop a generalization of the classical Euclidean algorithm, of independent interest per se. Introduction The problem of determining the number of zeros of a polynomial in a given region of the complex plane is very classical and goes back to Descartes, Gauss, Cauchy [4], Routh [22, 23], Hermite [9], Hurwitz [14], and many others. The entire second volume of the delightful Problems and Theorems in Analysis by P´olya and Szeg˝o[21] is devoted to this and related problems. See also comprehensive monographs of Marden [17], Obreshkoff [19], and Fisk [6]. One particularly famous late-19th-century result, which also has numerous applications, is the Routh- Hurwitz criterion of stability. Recall that a polynomial is called stable if all its zeros lie in the open left half-plane of the complex plane. The Routh-Hurwitz criterion asserts the following: Theorem 1 (Routh-Hurwitz [14, 22, 23]).
    [Show full text]
  • Critical Exponents: Old and New
    W&M ScholarWorks Undergraduate Honors Theses Theses, Dissertations, & Master Projects 5-2011 Critical Exponents: Old and New Olivia J. Walch College of William and Mary Follow this and additional works at: https://scholarworks.wm.edu/honorstheses Part of the Mathematics Commons Recommended Citation Walch, Olivia J., "Critical Exponents: Old and New" (2011). Undergraduate Honors Theses. Paper 423. https://scholarworks.wm.edu/honorstheses/423 This Honors Thesis is brought to you for free and open access by the Theses, Dissertations, & Master Projects at W&M ScholarWorks. It has been accepted for inclusion in Undergraduate Honors Theses by an authorized administrator of W&M ScholarWorks. For more information, please contact [email protected]. Critical exponents: Old and New A thesis submitted in partial fulfillment of the requirement for the degree of Bachelor of Science in Mathematics from The College of William and Mary by Olivia Walch Accepted for: Thesis director: CHARLES JOHNSON Panel Member 1: ILYA SPITKOVSKY Panel Member 2: JOSHUA ERLICH Williamsburg, VA May 13, 2011 Abstract Let P be a class of matrices, and let A be an m-by-n matrix in the class; consider some continuous powering, Aftg. The critical exponent of P, if it exists, with respect to the powering is the lowest power g(P) such that for any matrix B 2 P , Bftg 2 P 8 t > g(P). For powering relative to matrix multiplication in the traditional sense, hereafter referred to as conventional multiplication, t this means that A is in the specified class for all t > gC (P). For Hadamard (t) multiplication, similarly, A is in the class 8 t > gH (P).
    [Show full text]
  • CONFERENCE PROGRAM Monday, April 23 09:30–10:30
    CONFERENCE PROGRAM Monday, April 23 09:30–10:30 REGISTRATION 10:30–11:15 Pertti Mattila. Projections, Hausdorff dimension, and very little about analytic capacity. COFFEE BREAK 11:40–12:25 Arno Kuijlaars. The two-periodic Aztec diamond and matrix valued orthogonal polynomials. 12:35–13:20 Alexander Logunov. 0:01% improvement of the Liouville property for discrete harmonic functions on Z2. LUNCH Section A 15:00–15:25 Konstantin Dyakonov. Interpolating by functions from star-invariant subspaces. 15:30–15:55 Xavier Massaneda. Equidistribution and β-ensembles. Section B 15:00–15:25 Alexandre Sukhov. Analytic geometry of Levi-flat singularities. 15:30–15:55 Nikolai Kruzhilin. Proper maps of Reinhardt domains. COFFEE BREAK 1 Section A 16:25–16:50 St´ephaneCharpentier. Small Bergman–Orlicz and Hardy–Orlicz spaces. 16:55–17:20 Avner Kiro. Uniqueness theorems in non-isotropic Carleman classes. 17:25–17:50 Alexander Pushnitski. Weighted model spaces and Schmidt subspaces of Hankel operators. Section B 16:25–16:50 Vesna Todorˇcevi´c. Subharmonic behavior and quasiconformal mappings. 16:55–17:20 Nicola Arcozzi. Carleson measures for the Dirichlet spaces on the bidisc. 18:00 WELCOME PARTY at The Euler International Mathematical Institute 2 Tuesday, April 24 09:30–10:15 Armen Sergeev. Seiberg–Witten equations as a complex version of Ginzburg–Landau Equations. 10:25–11:10 Josip Globevnik. On complete complex hypersurfaces in CN . COFFEE BREAK 11:40–12:25 Alexander Aptekarev. Asymptotics of Hermite–Pad´e approximants of multi-valued analytic functions. 12:35–13:20 Frank Kutzschebauch. Factorization of holomorphic matrices in elementary factors.
    [Show full text]
  • 1 Definitions
    Xu Chen February 19, 2021 Outline • Preliminaries • Stability concepts • Equilibrium point • Stability around an equilibrium point • Stability of LTI systems • Method of eigenvalue/pole locations • Routh Hurwitz criteria for CT and DT systems • Lyapunov’s direct approach 1 Definitions 1.1 Finite dimensional vector norms Let v 2 Rn. A norm is: • a metric in vector space: a function that assigns a real-valued length to each vector in a vector space, e.g., p T p 2 2 2 – 2 (Euclidean) norm: kvk2 = v v = v1 + v2 + ··· + vn Pn – 1 norm: kvk1 = i=1 jvjj (absolute column sum) – infinity norm: kvk1 = maxi jvij Pn p 1=p – p norm: jjvjjp = ( i=1 jvij ) ; 1 ≤ p < 1 • default in this set of notes: k · k = k · k2 1.2 Equilibrium state For n-th order unforced system x_ = f (x; t) ; x(t0) = x0 an equilibrium state/point xe is one such that f (xe; t) = 0; 8t • the condition must be satisfied by all t ≥ 0. • if a system starts at equilibrium state, it stays there • e.g., (inverted) pendulum resting at the verticle direction • without loss of generality, we assume the origin is an equilibrium point 1.3 Equilibrium state of a linear system For a linear system x_(t) = A(t)x(t); x(t0) = x0 • origin xe = 0 is always an equilibrium state • when A(t) is nonsingular, multiple equilibrium states exist 1 Xu Chen 1.4 Continuous function February 19, 2021 Figure 1: Continuous functions Figure 2: Uniformly continuous (left) and continuous but not uniformly continuous (right) functions 1.4 Continuous function The function f : R ! R is continuous at x0 if 8 > 0, there exists a δ (x0; ) > 0 such that jx − x0j < δ =) jf (x) − f (x0)j < Graphically, continuous functions is a single unbroken curve: 2 1 x2−1 e.g., sin x, x , x−1 , x−1 , sign(x − 1:5) 1.5 Uniformly continuous function The function f : R ! R is uniformly continuous if 8 > 0, there exists a δ () > 0 such that jx − x0j < δ () =) jf (x) − f (x0)j < • δ is a function of not x0 but only 1.6 Lyapunov’s definition of stability • Lyapunov invented his stability theory in 1892 in Russia.
    [Show full text]
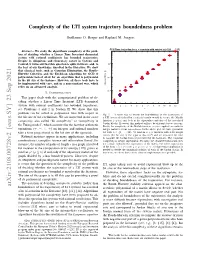
  • Complexity of the LTI System Trajectory Boundedness Problem
    Complexity of the LTI system trajectory boundedness problem Guillaume O. Berger and Raphael¨ M. Jungers CPU Time for jordan for n n matrix with entries in {-128, ,127} Abstract— We study the algorithmic complexity of the prob- lem of deciding whether a Linear Time Invariant dynamical system with rational coefficients has bounded trajectories. Despite its ubiquitous and elementary nature in Systems and Control, it turns out that this question is quite intricate, and, to 100 the best of our knowledge, unsolved in the literature. We show that classical tools, such as Gaussian Elimination, the Routh– Hurwitz Criterion, and the Euclidean Algorithm for GCD of polynomials indeed allow for an algorithm that is polynomial 10-1 in the bit size of the instance. However, all these tools have to be implemented with care, and in a non-standard way, which relies on an advanced analysis. elapsed time [s] 10-2 I. INTRODUCTION This paper deals with the computational problem of de- ciding whether a Linear Time Invariant (LTI) dynamical system with rational coefficients has bounded trajectories; 1 2 3 4 5 6 7 8 9 10 11 12 see Problems 1 and 2 in Section II. We show that this n problem can be solved in polynomial time with respect to Fig. 1. A naive way to decide the boundedness of the trajectories of the bit size of the coefficients. We are interested in the exact a LTI system described by a rational matrix would be to use the Matlab complexity, also called “bit complexity” or “complexity in function jordan and look at the eigenvalues and size of the associated Jordan blocks.
    [Show full text]
  • Permutation Matrices Whose Convex Combinations Are Orthostochastic
    View metadata, citation and similar papers at core.ac.uk brought to you by CORE provided by Elsevier - Publisher Connector Permutation Matrices Whose Convex Combinations Are Orthostochastic Yik-Hoi Au-Yeung and Che-Man Cheng Department of Mathematics University of Hong Kong Hong Kong Submitted by Richard A. Brualdi ABSTRACT Let P,, ., t’,,, be n x n permutation matrices. In this note, we give a simple necessary condition for all convex combinations of P,, . , Pm to be orthostochastic. We show that for n < 15 the condition is also sufficient, but for n > 15 whether the condition is suffkient or not is still open. 1. INTRODUCTION An n X n doubly stochastic (d.s.) matrix (aij> is said to be orthostochastic (o.s.) if there exists an n X n unitary matrix (a,,> such that aij = IuijJ2. OS. matrices play an important role in the consideration of generalized numerical ranges (for example, see [2]). For some other properties of OS. matrices see [4], [5], and [6]. For n > 3, it is known that there are d.s. matrices which are not 0.s. (for example, see [4]), and for n = 3 there are necessary and sufficient conditions for a d.s. matrix to be O.S. [2], but for n > 3 no such conditions have been obtained. We shall denote by II,, the group of all n x n permuta- tion matrices and by @n the set of all rr X n OS. matrices. Let P,, . , P,, E II,. We shall give a necessary condition for conv( P,, . , P,,,} c On, where “conv” means “convex hull of,” and then show that the same condition is also sufficient for n < I5.
    [Show full text]
  • Perron–Frobenius Theorem - Wikipedia
    Perron–Frobenius theorem - Wikipedia https://en.wikipedia.org/wiki/Perron–Frobenius_theorem Perron–Frobenius theorem In linear algebra, the Perron–Frobenius theorem, proved by Oskar Perron (1907) and Georg Frobenius (1912), asserts that a real square matrix with positive entries has a unique largest real eigenvalue and that the corresponding eigenvector can be chosen to have strictly positive components, and also asserts a similar statement for certain classes of nonnegative matrices. This theorem has important applications to probability theory (ergodicity of Markov chains); to the theory of dynamical systems (subshifts of finite type); to economics (Okishio's theorem,[1] Hawkins–Simon condition[2]); to demography (Leslie population age distribution model);[3] to social networks (DeGroot learning process), to Internet search engines[4] and even to ranking of football teams.[5] The first to discuss the ordering of players within tournaments using Perron– Frobenius eigenvectors is Edmund Landau.[6] [7] Contents Statement Positive matrices Non-negative matrices Classification of matrices Perron–Frobenius theorem for irreducible matrices Further properties Applications Non-negative matrices Stochastic matrices Algebraic graph theory Finite Markov chains Compact operators Proof methods Perron root is strictly maximal eigenvalue for positive (and primitive) matrices Proof for positive matrices Lemma Power method and the positive eigenpair Multiplicity one No other non-negative eigenvectors Collatz–Wielandt formula Perron projection as a limit: Ak/rk Inequalities for Perron–Frobenius eigenvalue Further proofs 1 of 18 2/8/19, 14:03 Perron–Frobenius theorem - Wikipedia https://en.wikipedia.org/wiki/Perron–Frobenius_theorem Perron projection Peripheral projection Cyclicity Caveats Terminology See also Notes References Original papers Further reading Statement Let positive and non-negative respectively describe matrices with exclusively positive real numbers as elements and matrices with exclusively non-negative real numbers as elements.
    [Show full text]