Multiphoton Ionization of Atoms and Ions by High Intensity X Ray Lasers
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Field Ionization in Short and Extremely Intense Laser Pulses
Field ionization in short and extremely intense laser pulses I. Yu. Kostyukov∗ and A. A. Golovanov Institute of Applied Physics, Russian Academy of Science, 46 Uljanov str., 603950 Nizhny Novgorod, Russia Modern laser systems are able to generate short and intense laser pulses ionizing matter in the poorly explored barrier-suppression regime. Field ionization in this regime is studied analytically and numerically. For analytical studies, both the classical and the quantum approaches are used. Two approximations to solve the time-dependent Schrödinger equation are proposed: the free electron approximation, in which the atomic potential is neglected, and the motionless approximation, in which only the external field term is considered. In the motionless approximation, the ionization rate in extremely strong fields is derived. The approximations are applied to several model potentials and are verified using numeric simulations of the Schrödinger equation. A simple formula of the ionization rate both for the tunnel and the barrier-suppression regimes is proposed. The formula can be used, for example, in particle-in-cell codes for simulations of the interaction of extremely intense laser fields with matter. PACS numbers: 79.70.+q, 03.65.-w I. INTRODUCTION is the ionization potential of the atom (ion), ωL is the laser frequency. The first two regimes are investigated Field ionization is one of the first processes which come theoretically in detail starting from the milestone paper into play at ultrahigh-intensity laser–matter interaction. by Keldysh [10]. It is generally believed [11–13] that for The peak power of some laser facilities exceeds the 5PW short and intense laser pulses the field ionization occurs level and will be doubled soon [1]. -

Chemical Potential Chem
EnergeticsEnergetics of of thethe Time-DependentTime-Dependent NaturalNatural OrbitalsOrbitals ofof MoleculesMolecules 1 2 1 3 HirohikoHirohiko Kono Kono11, ,Tsuyoshi Tsuyoshi Kato Kato22 , Takayuki,Takayuki Oyamada Oyamada11 , ,ShiroShiro Koseki Koseki33 1.1. Tohoku Tohoku Univ. Univ. 2. 2. Univ. Univ. of of Tok Tokyoyo 3. 3. Osaka Osaka Prefectural Prefectural Univ. Univ. Matsushima Bay (from Aoba-yama Campus in Sendai) Matsushima bay Tohoku U. (Sendai) Tokyo YITP, Kyoto, Sep. 28 (2011) Interaction of molecules with fs laser pulses (1) Radiative interaction: One-body interaction (fs or as regime) An electron or electrons get energy → Energy sharing by many electrons Development of MCTDHF in grid space T. Kato and H. Kono Characterization of multi-electron dynamics J. Chem. Phys. 128, 184102 (2008); by “time-dependent” chemical potential Chem. Phys. 366, 46 (2009). ・ Classification of adiabatic or nonadiabatic processes ・Quantification of energy exchange between molecular orbitals (2) Energy transfer to vibrational degrees of freedom (10-100 fs) Coupling of laser-induced ultrafast M. Kanno, H. Kono, Y. Fujimura, -electron rotations with vibrational modes and S. H. Lin in chiral aromatic molecules Phys. Rev. Lett. 104, 108302 (2010). (3)Intramolecular Vibrational Energy Redistribution (IVR) among different vibrational modes (1 ps –) →Rearrangement or reaction processes (ps –ns) Difficulties in the control of big molecules such as C60; fast IVR e.g., Initial mode selective vibrational excitation HowHow to to overcome: overcome: by intense -
![Arxiv:1902.02255V1 [Physics.Atom-Ph] 6 Feb 2019 fields [15, 16]](https://docslib.b-cdn.net/cover/2674/arxiv-1902-02255v1-physics-atom-ph-6-feb-2019-elds-15-16-1962674.webp)
Arxiv:1902.02255V1 [Physics.Atom-Ph] 6 Feb 2019 fields [15, 16]
Rydberg state ionization dynamics and tunnel ionization rates in strong electric fields K. Gawlas and S. D. Hogan Department of Physics and Astronomy, University College London, Gower Street, London WC1E 6BT, U.K. (Dated: February 7, 2019) Tunnel ionization rates of triplet Rydberg states in helium with principal quantum numbers close to 37 have been measured in electric fields at the classical ionization threshold of ∼ 197 V/cm. The measurements were performed in the time domain by combining high-resolution continuous-wave laser photoexcitation and pulsed electric field ionization. The observed tunnel ionization rates range from 105 s−1 to 107 s−1 and have, together with the measured atomic energy-level structure in the corresponding electric fields, been compared to the results of calculations of the eigenvalues of the Hamiltonian matrix describing the atoms in the presence of the fields to which complex absorbing potentials have been introduced. The comparison of the measured tunnel ionization rates with the results of these, and additional calculations for hydrogen-like Rydberg states performed using semi- empirical methods, have allowed the accuracy of these methods of calculation to be tested. For the particular eigenstates studied the measured ionization rates are ∼ 5 times larger than those obtained from semi-empirical expressions. I. INTRODUCTION collisions with ground state ammonia molecules [7, 8]. The experimental results have been compared with the Rydberg states of atoms and molecules represent ideal results of calculations performed using semi-empirical an- model systems with which to perform detailed studies of alytical methods for the treatment of hydrogen-like Ry- electric field ionization, and develop schemes with which dberg states with similar characteristics to those of the to manipulate and control ionization processes [1]. -

Electromagnetic-Radiation Effects on Alpha Decay
Electromagnetic-radiation effect on alpha decay M. Apostol Department of Theoretical Physics, Institute of Atomic Physics, Magurele-Bucharest MG-6, POBox MG-35, Romania email: [email protected] J. Math. Theor. Phys. 1 155 (2018) Abstract The effect of the electromagnetic radiation on the spontaneous charge emission from heavy atomic nuclei is estimated in a model which may be relevant for proton emission and alpha-particle decay in laser fields. Arguments are given that the electronic cloud in heavy atoms screens appreciably the electric field acting on the nucleus and the nucleus "sees" rather low fields. In these conditions, it is shown that the electromagnetic radiation brings second-order corrections in the electric field to the disintegration rate, with a slight anisotropy. These corrections give a small enhancement of the disintegration rate. The case of a static electric field is also discussed. arXiv:1809.10349v1 [nucl-th] 27 Sep 2018 PACS: 23.60.+e; 23.50.+z; 03.65.xp; 03.65.Sq; 03.50.de Key words: alpha decay; electromagnetic radiation; proton emission; laser radiation In the context of an active topical research in laser-related physics,[1]-[5] the problem of charge emission from bound-states under the action of the electromagnetic radiation is receiving an increasing interest. Some investi- gations focus especially on the effect the optical-laser radiation may have on the spontaneous alpha-particle decay of the atomic nuclei,[6]-[11] or nuclear 1 proton emission,[12, 13] but the area may be extended to atom ionization or molecular or atomic clusters fragmentation.[14]-[17] The aim of the present paper is to estimate the effect of the adiabatically-applied electromagnetic radiation upon the rate of spontaneous nuclear alpha decay and proton emis- sion. -
![Arxiv:1711.01875V3 [Physics.Atom-Ph] 4 Jul 2018](https://docslib.b-cdn.net/cover/6792/arxiv-1711-01875v3-physics-atom-ph-4-jul-2018-2526792.webp)
Arxiv:1711.01875V3 [Physics.Atom-Ph] 4 Jul 2018
Absolute strong-field ionization probabilities of ultracold rubidium atoms Philipp Wessels,1, 2, ∗ Bernhard Ruff,1, 2 Tobias Kroker,1, 2 Andrey K. Kazansky,3, 4, 5 Nikolay M. Kabachnik,1, 5, 6 Klaus Sengstock,1, 2 Markus Drescher,1, 2 and Juliette Simonet2 1The Hamburg Centre for Ultrafast Imaging, Luruper Chaussee 149, 22761 Hamburg, Germany 2Center for Optical Quantum Technologies, University of Hamburg, Luruper Chaussee 149, 22761 Hamburg, Germany 3Departamento de Fisica de Materiales, UPV/EHU, 20018 San Sebastian/Donostia, Spain 4Ikerbasque, Basque Foundation for Science, 48011 Bilbao, Spain 5Donostia International Physics Center (DIPC), 20018 San Sebastian/Donostia, Spain 6Skobeltsyn Institute of Nuclear Physics, Lomonosov Moscow State University, Moscow 119991, Russia (Dated: February 21, 2018) We report on precise measurements of absolute nonlinear ionization probabilities obtained by exposing optically trapped ultracold rubidium atoms to the field of an ultrashort laser pulse in the intensity range of 1 × 1011 to 4 × 1013 W/cm2. The experimental data are in perfect agreement with ab-initio theory, based on solving the time-dependent Schrödinger equation without any free parameters. Ultracold targets allow to retrieve absolute probabilities since ionized atoms become apparent as a local vacancy imprinted into the target density, which is recorded simultaneously. We study the strong-field response of 87Rb atoms at two different wavelengths representing non-resonant and resonant processes in the demanding regime where the Keldysh parameter is close to unity. Ultracold atoms serve as ideal systems for precise stud- creating electrons and ions on instantaneous time-scales ies of light-matter interaction with a high degree of con- with ultrashort laser pulses. -

From Multiphoton to Tunnel Ionization
249 Chapter 3 FROM MULTIPHOTON TO TUNNEL IONIZATION S. L. CHIN Canada Research Chair (Senior) Center for Optics, Photonics and Laser & Department of Physics, Engineering Physics and Optics Laval University, Quebec City, Quebec, G1K 7P4, Canada [email protected] The story of the development of multiphton ionization to tunnel ionization is told briefly from the experimental point of view. It stresses the physical idea of tunneling ionization and the practical use of some tunneling formulae to fit experimental data. ADK formula is not universally valid in spite of its popularity. Contents 1. Introduction 250 2. Laser Induced Breakdown 251 3. Multiphoton Ionization of Atoms (1964–1978) 253 4. A Persistent Challenge in the 1960s and 1970s: Tunnel Ionization 254 5. Some Surprises (1979–1989) 254 6. Tunnel Ionization using Long and Short Wavelength Lasers 261 7. Which Tunnel Ionization Formula to Use? 263 Conclusion 269 Acknowledgments 269 References 269 250 1. Introduction This is a personal account of the progress of high laser field physics in atoms and molecules. The author has experienced the entire development of this field of research from the very beginning of Q-switched laser induced breakdown of gases, multiphoton ionization (MPI) and tunnel ionization of atoms and molecules that continues into the current state of the control of molecules in ultrafast intense laser field, atto-second laser science, etc. The purpose of this review is to tell a brief story of the development from laser induced breakdown through multiphoton ionization to tunnel ionization. Emphasis will be given to: (1) the physics of tunnel ionization based on our experimental results using a CO2 laser; (2) the applicability of the concept of tunneling to ionization of atoms and molecules using intense femtosecond near i.r. -

Canonical Tunneling Time in Ionization Experiments Arxiv
Canonical Tunneling Time in Ionization Experiments Bekir Bayta¸s∗, Martin Bojowaldy and Sean Crowez Department of Physics, The Pennsylvania State University, 104 Davey Lab, University Park, PA 16802, USA Abstract Canonical semiclassical methods can be used to develop an intuitive definition of tunneling time through potential barriers. An application to atomic ionization is given here, considering both static and time-dependent electric fields. The results allow one to analyze different theoretical constructions proposed recently to evaluate ionization experiments based on attoclocks. They also suggest new proposals of determining tunneling times, for instance through the behavior of fluctuations. 1 Introduction Detailed observations of atom ionization have recently become possible with attoclock experiments [1, 2, 3], suggesting comparisons with various predictions of tunneling times. The theoretical side of the question, however, remains largely open: Different proposals of how to define tunneling times have been made through almost nine decades, yielding widely diverging predictions and physical interpretations [4, 5]. Even the extraction of tunneling times from experiments has been performed in different ways [6, 7, 8, 9, 10, 11], and the original conclusion of a non-zero result has been challenged [12, 13, 14]. The situation therefore remains far from being clarified, and a continuing analysis of fundamental aspects of tunneling is important. A recent approach to understand the tunneling dynamics in this context is the appli- cation of Bohmian quantum mechanics [15, 16], in which the prominent role played by trajectories provides a more direct handle on tunneling times [17]. However, through ini- tial conditions, the ensemble of trajectories remains subject to statistical fluctuations. -
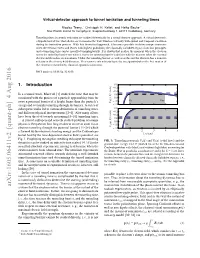
Virtual-Detector Approach to Tunnel Ionization and Tunneling Times
Virtual-detector approach to tunnel ionization and tunneling times Nicolas Teeny,∗ Christoph H. Keitel, and Heiko Baukey Max-Planck-Institut für Kernphysik, Saupfercheckweg 1, 69117 Heidelberg, Germany Tunneling times in atomic ionization are studied theoretically by a virtual detector approach. A virtual detector is a hypothetical device that allows one to monitor the wave function’s density with spatial and temporal resolution during the ionization process. With this theoretical approach, it becomes possible to define unique moments when the electron enters and leaves with highest probability the classically forbidden region from first principles and a tunneling time can be specified unambiguously. It is shown that neither the moment when the electron enters the tunneling barrier nor when it leaves the tunneling barrier coincides with the moment when the external electric field reaches its maximum. Under the tunneling barrier as well as at the exit the electron has a nonzero velocity in the electric field direction. This nonzero exit velocity has to be incorporated when the free motion of the electron is modeled by classical equations of motion. PACS numbers: 03.65.Xp, 32.80.Fb 1. Introduction 0.0 0.2 − (a.u.) 0.4 4 − In a seminal work, MacColl [1] studied the time that may be / 0.6 E , − ) 0.8 associated with the process of a particle approaching from far ξ ( − ξ ξ 1 1.0 in exit away a potential barrier of a height larger than the particle’s V − 1.2 energy and eventually tunneling through the barrier. A series of − subsequent works led to various definitions of tunneling times 0.0 0.2 and different physical interpretations [2–4]. -

Rydberg-State Ionization Dynamics and Tunnel Ionization Rates in Strong Electric fields
PHYSICAL REVIEW A 99, 013421 (2019) Rydberg-state ionization dynamics and tunnel ionization rates in strong electric fields K. Gawlas and S. D. Hogan Department of Physics and Astronomy, University College London, Gower Street, London, WC1E 6BT, United Kingdom (Received 2 November 2018; published 17 January 2019) Tunnel ionization rates of triplet Rydberg states in helium with principal quantum numbers close to 37 have been measured in electric fields at the classical ionization threshold of ∼197 V/cm. The measurements were performed in the time domain by combining high-resolution continuous-wave laser photoexcitation and pulsed electric field ionization. The observed tunnel ionization rates range from 105 to 107 s−1 and have, together with the measured atomic energy-level structure in the corresponding electric fields, been compared to the results of calculations of the eigenvalues of the Hamiltonian matrix describing the atoms in the presence of the fields to which complex absorbing potentials have been introduced. The comparison of the measured tunnel ionization rates with the results of these, and additional calculations for hydrogenlike Rydberg states performed using semiempirical methods, have allowed the accuracy of these methods of calculation to be tested. For the particular eigenstates studied the measured ionization rates are ∼5 times larger than those obtained from semiempirical expressions. DOI: 10.1103/PhysRevA.99.013421 I. INTRODUCTION ment and optimization of detection schemes used for studies of Förster resonance energy transfer in collisions with ground Rydberg states of atoms and molecules represent ideal state ammonia molecules [7,8]. The experimental results have model systems with which to perform detailed studies of been compared with the results of calculations performed electric field ionization, and develop schemes with which to using semiempirical analytical methods for the treatment of manipulate and control ionization processes [1]. -

Strong Field Phenomena in Atoms and Molecules from Near to Midinfrared Laser Fields
Strong Field Phenomena in Atoms and Molecules from near to midinfrared laser fields DISSERTATION Presented in Partial Fulfillment of the Requirements for the Degree Doctor of Philosophy in the Graduate School of The Ohio State University By Yu Hang Lai, B.S. Graduate Program in Physics The Ohio State University 2018 Dissertation Committee: Dr. Louis F. DiMauro, Advisor Dr. Enam Chowdhury Dr. Ulrich Heinz Dr. Ezekiel Johnston-Halperin ⃝c Copyright by Yu Hang Lai 2018 Abstract paraStrong field atomic physics is the study of the interaction between an atom andan intense laser pulse such that the field strength is \not-so-small" compared to an atomic unit (50 V/A)˚ and so it could not be treated as just a perturbation to the atomic system. Depending upon the ionization potential of the target, typical laser intensity required to reach this regime ranging from ∼ 10 to 1000 TW/cm2. In the low frequency limit, the photoionization process can be interpreted as a tunneling process in which the atomic potential is \tilted" by the laser field allowing the electron to escape via quantum tunneling. The escaped electron wavepacket quivers in the strong laser field whose kinetic energy is characterized by the ponderomotive energy Up which is proportional to the laser intensity and the square of the wavelength. Electron recollision happens when the ionized electron is driven back towards its parent ion by the laser field and it leads to numerous intriguing phenomena such as high-order above-threshold ionization, non-sequential ionization and high-order harmonic generation. While most of the early experiments were performed in the near-infrared (NIR)(0.8 or 1 µm) wavelengths, an important advance over the last decade has been the emergence of intense mid-infrared (MIR)(∼ 2 − 4 µm) sources. -

Tunneling Ionization of Atoms Christer Z
Tunneling ionization of atoms Christer Z. Bisgaard and Lars Bojer Madsen Citation: American Journal of Physics 72, 249 (2004); doi: 10.1119/1.1603274 View online: http://dx.doi.org/10.1119/1.1603274 View Table of Contents: http://scitation.aip.org/content/aapt/journal/ajp/72/2?ver=pdfcov Published by the American Association of Physics Teachers Articles you may be interested in Ionization and dissociation dynamics of vinyl bromide probed by femtosecond extreme ultraviolet transient absorption spectroscopy J. Chem. Phys. 140, 064311 (2014); 10.1063/1.4865128 Theoretical studies on tunneling ionizations of helium atom in intense laser fields J. Chem. Phys. 124, 144303 (2006); 10.1063/1.2183300 Ionization of Argon n =2 ( Ar +9 to Ar +16 ) by a “relativistic” laser field AIP Conf. Proc. 525, 667 (2000); 10.1063/1.1291983 Double ionization of a two-electron model atom in a single-cycle laser pulse AIP Conf. Proc. 525, 176 (2000); 10.1063/1.1291937 Calculating the Keldysh adiabaticity parameter for atomic, diatomic, and polyatomic molecules J. Chem. Phys. 108, 7739 (1998); 10.1063/1.476208 This article is copyrighted as indicated in the article. Reuse of AAPT content is subject to the terms at: http://scitation.aip.org/termsconditions. Downloaded to IP: 157.92.4.72 On: Tue, 19 Jan 2016 18:04:11 Tunneling ionization of atoms Christer Z. Bisgaard and Lars Bojer Madsena) Department of Physics and Astronomy, University of Aarhus, 8000 A˚ rhus C, Denmark ͑Received 24 February 2003; accepted 23 June 2003͒ We discuss the theory for the ionization of atoms by tunneling due to a strong external static electric field or an intense low frequency laser field. -

Dynamical Core Polarization of Two-Active-Electron Systems In
Dynamical core polarization of two-active-electron systems in strong laser fields Zengxiu Zhao∗ and Jianmin Yuan Department of Physics, National University of Defense Technology, Changsha 410073, P. R. China (Dated: July 25, 2018) The ionization of two-active-electron systems by intense laser fields is investigated theoretically. In comparison with time-dependent Hartree-Fock and exact two electron simulation, we show that the ionization rate is overestimated in SAE approximation. A modified single-active-electron model is formulated by taking into account of the dynamical core polarization. Applying the new approach to Ca atoms, it is found that the polarization of the core can be considered instantaneous and the large polarizability of the cation suppresses the ionization by 50% while the photoelectron cut-off energy increases slightly. The existed tunneling ionization formulation can be corrected analytically by considering core polarization. PACS numbers: 33.80.Rv, 42.50.Hz, 42.65.Re Various of non-perturbative phenomena occurring dur- time-varying. In the case of absence of resonant exci- ing atom-laser interactions are started with single ion- tation, the polarization is instantaneously following the ization, e.g., above threshold ionization (ATI) and high laser field. One therefore expects that ionization rates harmonic generation (HHG). Although they have been from single-active electron theory needed to be corrected successfully interpreted by the rescattering model based by taking the dynamical core-polarization (DCP) into on single active electron (SAE) approximation (see Re- account [12]. Recently we have incorporated the DCP views e.g., [1, 2]), detailed examination showed that mul- into simulations [13] successfully interpreting the exper- tielectron effects are embedded in the photon and elec- imentally measured alignment-dependent ionization rate tron spectra [3–9].