DOCSLIB.ORG

Atlas of Three Body Mean Motion Resonances in the Solar System

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Atlas of Three Body Mean Motion Resonances in the Solar System Icarus 231 (2014) 273–286 Contents lists available at ScienceDirect Icarus journal homepage: www.elsevier.com/locate/icarus Atlas of three body mean motion resonances in the Solar System Tabaré Gallardo Departamento de Astronomía, Instituto de Física, Facultad de Ciencias, Universidad de la República, Iguá 4225, 11400 Montevideo, Uruguay article info abstract Article history: We present a numerical method to estimate the strengths of arbitrary three body mean motion reso- Received 22 July 2013 nances between two planets in circular coplanar orbits and a massless particle in an arbitrary orbit. This Revised 14 December 2013 method allows us to obtain an atlas of the three body resonances in the Solar System showing where are Accepted 17 December 2013 located and how strong are thousands of resonances involving all the planets from 0 to 1000 au. This atlas Available online 27 December 2013 confirms the dynamical relevance of the three body resonances involving Jupiter and Saturn in the aster- oid belt but also shows the existence of a family of relatively strong three body resonances involving Ura- Keywords: nus and Neptune in the far Trans-Neptunian region and relatively strong resonances involving terrestrial Asteroids, dynamics and jovian planets in the inner planetary system. We calculate the density of relevant resonances along Celestial mechanics Resonances, orbital the Solar System resulting that the main asteroid belt is located in a region of the planetary system with Kuiper belt the lowest density of three body resonances. The method also allows the location of the equilibrium points showing the existence of asymmetric librations (r – 0 or 180). We obtain the functional depen- dence of the resonance’s strength with the order of the resonance and the eccentricity and inclination of the particle’s orbit. We identify some objects evolving in or very close to three body resonances with Earth–Jupiter, Saturn–Neptune and Uranus–Neptune apart from Jupiter–Saturn, in particular the NEA 2009 SJ18 is evolving in the resonance 1 À 1E À 1J and the centaur 10199 Chariklo is evolving under the influence of the resonance 5 À 2S À 2N. Ó 2013 Elsevier Inc. All rights reserved. 1. Introduction critical angles, identified thousands of asteroids in TBRs with Jupi- ter and Saturn, concluding there are more asteroids in TBRs than in Fifteen years ago, concentrated over a period of about a year, a two body resonances. succession of papers were published (Murray et al., 1998; Nesv- The approximate nominal position in semimajor axis of the orny´ and Morbidelli, 1998, 1999; Morbidelli and Nesvorny´ , 1999) TBRs taking arbitrary pairs of planets is very simple if we ignore showing an intense theoretical and numerical work on three body the secular motion of the perihelia and nodes of the three bodies. mean motion resonances (TBRs) involving an asteroid and two When these slow secular motions are taken into account each of massive planets. These papers, that have their roots on earlier the nominal TBRs split in a multiplet of resonances all them very works devoted to the study of an asteroid in zero order TBRs near the nominal one (Morbidelli, 2002). The challenge is to obtain (Wilkens, 1933; Okyay, 1935; Aksnes, 1988), stated the relevance the strength, width or libration timescale that give us the dynam- that the TBRs involving Jupiter–Saturn and also Mars–Jupiter have ical relevance of these resonances. Analytical planar theories in the long term stability in the asteroid’s region. In spite of being developed by Murray et al. (1998) and Nesvorny´ and Morbidelli weaker than the two body resonances they are much more numer- (1999) allowed to describe and understand the dynamics of the ous generating several dynamical features in the asteroidal popu- TBRs involving Jupiter and Saturn in the asteroidal region. These lation, like concentrations for some values of semimajor axes, theories are appropriated to study in detail specific resonances anomalous amplitude librations and chaotic evolutions (Nesvorny´ with Jupiter and Saturn but its application to any arbitrary reso- and Morbidelli, 1998). In particular, both borders of the main aster- nance involving any planet is not trivial, which possibly explains oid belt exhibit chaotic diffusion due to the superposition of the absence of papers published on this topic since these years several weak two-body and TBRs (Murray and Holman, 1997; with the exceptions of a few ones devoted to specific scenarios Morbidelli and Nesvorny´ , 1999). More recently, Smirnov and (Guzzo, 2005; de La Fuente Marcos and de La Fuente Marcos, Shevchenko (2013) in a massive numerical integration of 249,567 2008; Cachucho et al., 2010; Quillen, 2011). asteroids by 105 years and looking at the time evolution of the In this paper, from a different approach, we will obtain a global view of all dynamically relevant TBRs involving all the planets ta- ken by pairs along all the Solar System. Our method is not E-mail address: gallardo@fisica.edu.uy analytical but numerical and it is based on an estimation of the 0019-1035/$ - see front matter Ó 2013 Elsevier Inc. All rights reserved. http://dx.doi.org/10.1016/j.icarus.2013.12.020 274 T. Gallardo / Icarus 231 (2014) 273–286 1-2J+1S, e=0.0 1-2J+1S, e=0.1 ) ) σ σ ( ( ρ ρ 0 90 180 270 360 0 90 180 270 360 σ σ 1-2J+1S, e=0.2 1-2J+1S, e=0.3 ) ) σ σ ( ( ρ ρ 0 90 180 270 360 0 90 180 270 360 σ σ 1-2J+1S, e=0.4 1-2J+1S, e=0.5 ) ) σ σ ( ( ρ ρ 0 90 180 270 360 0 90 180 270 360 σ σ Fig. 1. Evolution of the shape of qðrÞ for growing eccentricities for the zero order resonance 1-2J + 1S at a ¼ 3:8045 au. Numerical integrations of test particles show that the asymmetric librations around r 90 and r 270 are stable and also exist large amplitude librations around r ¼ 180 that wrap both asymmetric libration centers. The librations around r ¼ 0 are unstable. strength of the resonances which is obtained evaluating the effects is oscillating over time, being ki the mean longitudes and ki integers. of the mutual perturbations in all possible spatial configurations of More precisely, for massless particles with inclined orbits there are the three bodies satisfying the resonant condition. It allows us to other possible definitions for the critical angle involving combina- appreciate the effect of arbitrary eccentricity and inclination of tions of its X0 and -0, but it is possible to show that after an appro- the massless particle’s orbit on the resonance’s strength but, in or- priate averaging procedure the leading term in the expansion of the der to reduce the number of parameters involved in the problem, resulting disturbing function will be the one whose argument is gi- we impose coplanar and circular orbits for the two perturbing ven by Eq. (1) (Nesvorny´ and Morbidelli, 1999). In this work we will planets. Nevertheless, the method can be extended to arbitrary use the following notation: the order of the resonance is planetary orbits. In the next section we start describing our numer- q ¼jk0 þ k1 þ k2j, we call p ¼jk0jþjk1jþjk2j and we note ical method and we explore how the calculated strengths depend k0 þ k1P1 þ k2P2 the resonance involving planets P1 and P2. The on the parameters of the problem. In Section 3 we analyze the approximate nominal location of the resonance assuming unper- distribution of TBRs along the Solar System and discuss its turbed Keplerian motions is dynamical effects providing some examples. In Section 4 we qffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi qffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi present the conclusions. À3=2 k1 3 k2 3 a0 ’ ð1 þ m1Þ=a1 À ð1 þ m2Þ=a2 ð2Þ k0 k0 2. Numerical approximation to the disturbing function for three body resonances where ai and mi are the mean semimajor axes of the planets and its masses expressed in solar masses respectively. In the real Solar Sys- Three body resonances between a massless particle with an tem the actual location depends on the precession of the perihelia arbitrary orbit given by ða0; e; i; X0; -0Þ and two planets P1 and P2 and the gravitational effects of the other planets not taken into in circular coplanar orbits occur when the critical angle account. In the very far Trans-Neptunian Region (TNR), depending on the resonance, the actual location could be shifted something r ¼ k k þ k k þ k k ðk þ k þ k Þ- ð1Þ 0 0 1 1 2 2 0 1 2 0 between 0.1 au and 1 au. T. Gallardo / Icarus 231 (2014) 273–286 275 1-3J+1S, e=0.01 1-3J+1S, e=0.1 ) ) σ σ ( ( ρ ρ 0 90 180 270 360 0 90 180 270 360 σ σ 1-3J+1S, e=0.2 1-3J+1S, e=0.3 ) ) σ σ ( ( ρ ρ 0 90 180 270 360 0 90 180 270 360 σ σ 1-3J+1S, e=0.4 1-3J+1S, e=0.5 ) ) σ σ ( ( ρ ρ 0 90 180 270 360 0 90 180 270 360 σ σ Fig. 2. Evolution of the shape of qðrÞ for growing eccentricities for the first order resonance 1-3J + 1S at a ¼ 2:7518 au, the resonance where is evolving 485 Genua. For large eccentricities asymmetric equilibrium points appear, which are stable according to numerical integrations of test particles. There are also large amplitude librations around r ¼ 180 that wrap both asymmetric libration centers. 2.758 2.756 2.754 2.752 2.75 mean a (au) 2.748 360 270 180 (1-3J+1S) σ 90 0 0 5000 10000 15000 20000 25000 30000 35000 40000 time (yrs) Fig.
Load more

Recommended publications
  • The Basic Physics of the Binary Black Hole Merger GW150914
    September 21, 2016 The basic physics of the binary black hole merger GW150914 The LIGO Scientific Collaboration and The Virgo Collaboration¤ The first direct gravitational-wave detection was made by the Advanced Laser Interferometer Gravitational Wave Observatory on September 14, 2015. The GW150914 signal was strong enough to be apparent, without using any waveform model, in the filtered detec- tor strain data. Here those features of the signal visible in these data are used, along with only such concepts from Newtonian physics and general relativity as are ac- cessible to anyone with a general physics background. The simple analysis presented here is consistent with the fully general-relativistic analyses published else- Figure 1 The instrumental strain data in the Livingston detec- where, in showing that the signal was produced by the tor (blue) and Hanford detector (red), as shown in Figure 1 of inspiral and subsequent merger of two black holes. The [1]. Both have been bandpass- and notch-filtered. The Hanford black holes were each of approximately 35M , still strain has been shifted back in time by 6.9 ms and inverted. ¯ Times shown are relative to 09:50:45 Coordinated Universal orbited each other as close as 350 km apart and sub- » Time (UTC) on September 14, 2015. sequently merged to form a single black hole. Similar reasoning, directly from the data, is used to roughly es- timate how far these black holes were from the Earth, A black hole is a region of space-time where the gravita- and the energy that they radiated in gravitational waves.
    [Show full text]
  • IDL-1426.Pdf
    The International Development Research Centre is a public corporation created by the Parliament of Canada in 1970 to support research designed to adapt science and technology to the needs of developing countries. The Centre's activity is concentrated in five sectors: agriculture, food and nutrition sciences; health sciences; information sciences; communications; and social sciences. IDRC is financed solely by the Government of Canada; its policies, however, are set by an international Board of Governors. The Centre's headquarters are in Ottawa, Canada. Regional offices are located in Africa, Asia, Latin America, and the Middle East. ©1978 International Development Research Centre Postal Address: Box 8500, Ottawa, Canada KlG 3H9 Head Office: 60 Queen Street, Ottawa Ronald, K. Selley, L.J. Amoroso, E.C. IDRC IDRC-TS13e Biological synopsis of the manatee. Ottawa, IDRC, 1978. 112 p. /IDRC publication/. Monograph on the manatee, an aquatic mammal (/animal species/) of the /tropical zone/s of I Africa south of Sahara/ and /Latin America/, with an extensive /bibliography/ - discusses the /classification/ of the species and subspecies of the genus Trichechus; /morphology/, /physiology/, /behaviour/, /reproduction/, /animal ecology/ (role in /aquatic plant/ /weed control/), and measures for /animal protection/ of the manatee. UDC: 599.55 ISBN: 0-88936-168-1 Microfiche edition available IDRC-TS13e Biological Synopsis of the Manatee K. Ronald, L.J. Selley, and E.C. Amoroso1 College ofBiological Science, University of Guelph, Guelph, Ontario 1 Present address: Agricultural Research Council, Institute of Animal Physiology, Babraham, Cambridge, England. This work was carried out with the aid of a grant from the International Development Research Centre.
    [Show full text]
  • (K)Cudos at Ψtucson
    (K)CUDOs at ΨTucson Work based on collaborative effort with present/former AZ students: Jeremiah Birrell and Lance Labun with contributions from exchange student from Germany Ch. Dietl. Johann Rafelski (UA-Physics) (K)CUDOS at ΨTucson PSITucson,April11,2013 1/39 1. Introduction 2. Dark Matter (CDM) Generalities 3. Strangeletts 4. Dark Matter (DM) CUDOs 5. CUDO impacts Johann Rafelski (UA-Physics) (K)CUDOS at ΨTucson PSITucson,April11,2013 2/39 kudos (from Greek kyddos, singular) = honor; glory; acclaim; praise kudo = back formation from kudos construed as a plural cud (Polish, pronounced c-ood) = miracle cudo (colloq. Polish) = of surprising and exceptional character CUDO=Compact UltraDense Object: A new opportunity to search for dark matter. Not dark matter in form of elementary particles (all present day searches) but (self) bound dark matter. Either an ultra-compact impactor or/and condensation seed for comets. There is a lot of dark matter around, cosmological abundance limit shown below. Johann Rafelski (UA-Physics) (K)CUDOS at ΨTucson PSITucson,April11,2013 3/39 A new type of meteors What if there are ‘dark’ matter meteor and asteroid-like bodies in the Universe? Could some of them have collided with solar system bodies and the Earth? Are they dressed in visible matter from prior impacts and as condensation seeds? CUDOs’ high density of gravitating matter provides the distinct observable, the surface-penetrating puncture: shot through Only a fraction of the kinetic energy damaging the solid surface. Johann Rafelski (UA-Physics) (K)CUDOS at ΨTucson PSITucson,April11,2013 4/39 Asteroids of high density Fruitful Discussions with Marshall Eubanks lead to these data.
    [Show full text]
  • Asteroid Spin Axes
    ASTEROID SPIN AXES Asteroid Q Period Amp L1 B1 L2 B2 L3 B3 L4 B4 Sid. period Mod Reference 1 Ceres 9.074170 0.06 332.0 70.0 Saint-Pe, 93 298.0 78.0 186.6 −58.0 Drummond, 98 3 322.0 78.0 Thomas, 05 352.0 80.0 Drummond, 08 346.0 82.0 Drummond, 14 2 Pallas 7.8132 0.16 228.0 43.0 7.8106 Schroll, 76 211.0 38.0 Burchi, 83 200.0 40.0 220.0 15.0 Binzel, 84 44.0 4.0 148.0 55.0 224.0 −4.0 328.0 −55.0 Zappala, 84 49.0 6.0 157.0 53.0 229.0 −6.0 337.0 −53.0 Burchi, 85 54.0 −6.0 7.813 Magnusson, 86 100.0 −22.0 295.0 16.0 Y Drummond, 89 70.0 15.0 250.0 15.0 70.0 −15.0 250.0 −15.0 Y Drummond, 89 3 193.0 43.0 35.0 −12.0 7.813224 Y Torppa, 03 32.0 −21.0 Drummond, 08 3 35.6 −12.6 193.1 44.2 7.813225 Y Higley, 08 2 34.0 −27.0 Y Drummond, 09 3 30.0 −16.0 Y Carry, 10 3 35.0 −12.0 7.81323 Durech, 11 3∗Juno 7.210 0.22 71.0 49.0 7.213 Chang, 62 101.0 29.0 321.0 57.0 141.0 −57.0 281.0 −29.0 Y Zappala, 84 110.0 40.0 7.210 Magnusson, 86 104.0 36.0 316.0 62.0 7.209526 Birch, 89 108.0 34.0 7.20953 Y Erikson, 93 108.0 38.0 7.20953 Y Dotto, 95 3 103.0 27.0 7.209531 Y Kaasalainen, 02 118.0 30.0 Drummond, 08 3 103.0 27.0 7.209531 Durech, 11 103.0 22.0 7.20953091 Y Viikinkoski, 15 104.0 20.0 7.209532 Hanus, 16 4 Vesta 5.342 0.19 14.0 80.0 5.3448 Cailliate, 56 10.689 Y Haupt, 58 57.0 74.0 5.34212 Chang, 62 126.0 65.0 5.342129 Gehrels, 67 139.0 47.0 333.0 39.0 10.6824 Taylor, 73 103.0 43.0 301.0 33.0 5.34213 Taylor, 85 120.0 65.0 325.0 55.0 5.342124 Y Magnusson, 86 85.0 58.0 310.0 60.0 Y Cellino, 87 336.0 55.0 5.3421 Y Drummond, 88 311.0 67.0 Y Drummond, 89 160.0 52.0 340.0
    [Show full text]
  • Broadband Photometry of the Potentially Hazardous Asteroid (153958) 2002 AM31: a Binary Near-Earth Asteroid
    Broadband Photometry of the Potentially Hazardous Asteroid (153958) 2002 AM31: A Binary Near-Earth Asteroid Tamara Davtyan¹, Michael D Hicks² 1-Los Angeles City College, Los Angeles, CA 2-Jet Propulsion Laboratory, Pasadena, CA Abstract The near-Earth asteroid 153958 (2002 AM31) was discovered on January 14, 2002 by the LINEAR NEO survey (MPEC 2002-A102) in New Mexico. The object passed within 0.035 AU of the Earth on July 22 2012 and has been identified as a Potentially Hazardous Asteroid (PHA) by the IAU Minor Planet Center. We were motivated by the PHA's favorable 2012 apparition and obtained 6 nights of time-resolved Bessel BVRI photometry and 5 nights of Bessel R photometry at the JPL Table Mountain Observatory (TMO) 0.6-m telescope. We generated a solar phase curve that was used to fit a standard H-G model ( H R=18.43, G=0.61). The derived G value was found to indicate a high optical albedo and an E-type classification. However, our observations yielded that the object's averaged broad-band colors indices ( B− R=0.217±0.018 mag; V −R=0.066±0.010 mag, R− I=0.001±0.110 mag) were most compatible with an S-type spectral classification (Bus taxonomy). This association obtained through a comparison with the 1341 asteroid spectra collected by SMASS 2 survey (Bus & Binzel 2002) and was best matched by the S-type asteroid 485 Genua. If we adopt a diameter of 0.34 km obtained by Arecibo radar imaging, then we estimate geometric albedo p=0.61.
    [Show full text]
  • The Planetary and Lunar Ephemeris DE 421
    IPN Progress Report 42-178 • August 15, 2009 The Planetary and Lunar Ephemeris DE 421 William M. Folkner,* James G. Williams,† and Dale H. Boggs† The planetary and lunar ephemeris DE 421 represents updated estimates of the orbits of the Moon and planets. The lunar orbit is known to submeter accuracy through fitting lunar laser ranging data. The orbits of Venus, Earth, and Mars are known to subkilometer accu- racy. Because of perturbations of the orbit of Mars by asteroids, frequent updates are needed to maintain the current accuracy into the future decade. Mercury’s orbit is determined to an accuracy of several kilometers by radar ranging. The orbits of Jupiter and Saturn are determined to accuracies of tens of kilometers as a result of spacecraft tracking and modern ground-based astrometry. The orbits of Uranus, Neptune, and Pluto are not as well deter- mined. Reprocessing of historical observations is expected to lead to improvements in their orbits in the next several years. I. Introduction The planetary and lunar ephemeris DE 421 is a significant advance over earlier ephemeri- des. Compared with DE 418, released in July 2007,1 the DE 421 ephemeris includes addi- tional data, especially range and very long baseline interferometry (VLBI) measurements of Mars spacecraft; range measurements to the European Space Agency’s Venus Express space- craft; and use of current best estimates of planetary masses in the integration process. The lunar orbit is more robust due to an expanded set of lunar geophysical solution parameters, seven additional months of laser ranging data, and complete convergence.
    [Show full text]
  • The Minor Planet Bulletin, We Feel Safe in Al., 1989)
    THE MINOR PLANET BULLETIN OF THE MINOR PLANETS SECTION OF THE BULLETIN ASSOCIATION OF LUNAR AND PLANETARY OBSERVERS VOLUME 43, NUMBER 3, A.D. 2016 JULY-SEPTEMBER 199. PHOTOMETRIC OBSERVATIONS OF ASTEROIDS star, and asteroid were determined by measuring a 5x5 pixel 3829 GUNMA, 6173 JIMWESTPHAL, AND sample centered on the asteroid or star. This corresponds to a 9.75 (41588) 2000 SC46 by 9.75 arcsec box centered upon the object. When possible, the same comparison star and check star were used on consecutive Kenneth Zeigler nights of observation. The coordinates of the asteroid were George West High School obtained from the online Lowell Asteroid Services (2016). To 1013 Houston Street compensate for the effect on the asteroid’s visual magnitude due to George West, TX 78022 USA ever changing distances from the Sun and Earth, Eq. 1 was used to [email protected] vertically align the photometric data points from different nights when constructing the composite lightcurve: Bryce Hanshaw 2 2 2 2 George West High School Δmag = –2.5 log((E2 /E1 ) (r2 /r1 )) (1) George West, TX USA where Δm is the magnitude correction between night 1 and 2, E1 (Received: 2016 April 5 Revised: 2016 April 7) and E2 are the Earth-asteroid distances on nights 1 and 2, and r1 and r2 are the Sun-asteroid distances on nights 1 and 2. CCD photometric observations of three main-belt 3829 Gunma was observed on 2016 March 3-5. Weather asteroids conducted from the George West ISD Mobile conditions on March 3 and 5 were not particularly favorable and so Observatory are described.
    [Show full text]
  • Download Full Issue
    THE MINOR PLANET BULLETIN OF THE MINOR PLANETS SECTION OF THE BULLETIN ASSOCIATION OF LUNAR AND PLANETARY OBSERVERS VOLUME 47, NUMBER 1, A.D. 2020 JANUARY-MARCH 1. SECTION NEWS: COLLABORATIVE ASTEROID PHOTOMETRY FOR STAFFING CHANGES FOR ASTEROID 2051 CHANG THE MINOR PLANET BULLETIN Alessandro Marchini Frederick Pilcher Astronomical Observatory, DSFTA - University of Siena (K54) Minor Planets Section Recorder Via Roma 56, 53100 - Siena, ITALY [email protected] [email protected] One staffing change and one staffing addition for The Minor Planet Bulletin are announced effective with this issue. Riccardo Papini, Massimo Banfi, Fabio Salvaggio Wild Boar Remote Observatory (K49) MPB Distributor Derald Nye is now retired from his 37 years of San Casciano in Val di Pesa (FI), ITALY service to the Minor Planets Bulletin. Derald stepped in to service at the time the MPB made its transition from the original Editor Melissa N. Hayes-Gehrke, Eric Yates and Section founder, Richard G. Hodgson. As Derald reflected in Department of Astronomy, University of Maryland a short essay written in MPB 40, page 53 (2013), the Distributor College Park, MD, USA 20740 position was the longest job he ever held, having retired from being a programmer for 30 years with IBM. (Work for IBM (Received: 2019 October 15) included programming for the space program.) At its peak, Derald was managing nearly 200 subscriptions. That number dropped to Photometric observations of this main-belt asteroid were the dozen or so libraries maintaining a permanent collection conducted in order to determine its rotation period. The following the MPB transitioning to becoming an on-line electronic authors found a synodic rotation period of 12.013 ± journal with limited printing.
    [Show full text]
  • The Basic Physics of the Binary Black Hole Merger GW150914
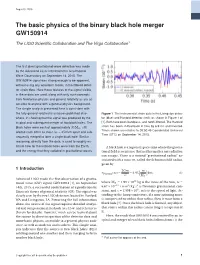
    August 5, 2016 The basic physics of the binary black hole merger GW150914 The LIGO Scientific Collaboration and The Virgo Collaboration¤ The first direct gravitational-wave detection was made by the Advanced Laser Interferometer Gravitational Wave Observatory on September 14, 2015. The GW150914 signal was strong enough to be apparent, without using any waveform model, in the filtered detec- tor strain data. Here those features of the signal visible in these data are used, along with only such concepts from Newtonian physics and general relativity as are ac- cessible to anyone with a general physics background. The simple analysis presented here is consistent with the fully general-relativistic analyses published else- Figure 1 The instrumental strain data in the Livingston detec- where, in showing that the signal was produced by the tor (blue) and Hanford detector (red), as shown in Figure 1 of inspiral and subsequent merger of two black holes. The [1]. Both have been bandpass- and notch-filtered. The Hanford black holes were each of approximately 35M , still strain has been shifted back in time by 6.9 ms and inverted. ¯ Times shown are relative to 09:50:45 Coordinated Universal orbited each other as close as 350 km apart and sub- » Time (UTC) on September 14, 2015. sequently merged to form a single black hole. Similar reasoning, directly from the data, is used to roughly es- timate how far these black holes were from the Earth, A black hole is a region of space-time where the gravita- and the energy that they radiated in gravitational waves.
    [Show full text]
  • Asteroid Spin Axes
    ASTEROID SPIN AXES Asteroid Q Period Amp L1 B1 L2 B2 L3 B3 L4 B4 Sid. period Mod Reference 1 Ceres 3 9.074170 0.06 332.0 +70.0 N Saint-Pe, 93 298.0 +78.0 186.6 −58.0 N Drummond, 98 3 322.0 +78.0 N Thomas, 05 352.0 +80.0 N Drummond, 08 346.0 +82.0 N Drummond, 14 2∗Pallas 3 7.8132 0.16 228.0 +43.0 7.8106 N Schroll, 76 211.0 +38.0 N Burchi, 83 200.0 +40.0 220.0 +15.0 N Binzel, 84 44.0 +4.0 148.0 +55.0 224.0 −4.0 328.0 −55.0 N Zappala, 84 49.0 +6.0 157.0 +53.0 229.0 −6.0 337.0 −53.0 N Burchi, 85 54.0 −6.0 7.813 N Magnusson, 86 100.0 −22.0 295.0 +16.0 Y Drummond, 89 70.0 +15.0 250.0 +15.0 70.0 −15.0 250.0 −15.0 Y Drummond, 89 3 35.0 −12.0 193.0 +43.0 7.813225 Y Torppa, 03 32.0 −21.0 N Drummond, 08 3 35.6 −12.6 193.1 +44.2 7.813225 Y Higley, 08 2 34.0 −27.0 Y Drummond, 09 3 30.0 −16.0 7.8132214 Y Carry, 10 3 35.0 −12.0 7.81323 Durech, 11 30.0 −13.0 7.81322 Y Hanus, 17 3 Juno 3 7.210 0.22 71.0 +49.0 7.213 N Chang, 62 101.0 +29.0 321.0 +57.0 141.0 −57.0 281.0 −29.0 Y Zappala, 84 110.0 +40.0 7.210 N Magnusson, 86 104.0 +36.0 316.0 +62.0 7.209526 N Birch, 89 108.0 +34.0 7.20953 Y Erikson, 93 108.0 +38.0 7.20953 Y Dotto, 95 3 103.0 +27.0 7.209531 Y Kaasalainen, 02 118.0 +30.0 N Drummond, 08 3 103.0 +27.0 7.209531 Durech, 11 103.0 +22.0 7.20953091 Y Viikinkoski, 15 104.0 +20.0 7.209532 Hanus, 16 4 Vesta 3 5.342 0.19 14.0 +80.0 5.3448 N Cailliate, 56 10.689 Y Haupt, 58 57.0 +74.0 5.34212 N Chang, 62 126.0 +65.0 5.342129 N Gehrels, 67 139.0 +47.0 333.0 +39.0 10.6824 N Taylor, 73 103.0 +43.0 301.0 +33.0 5.34213 N Taylor, 85 120.0 +65.0 325.0 +55.0 5.342124
    [Show full text]
  • The Planetary and Lunar Ephemerides DE430 and DE431
    IPN Progress Report 42-196 • February 15, 2014 The Planetary and Lunar Ephemerides DE430 and DE431 William M. Folkner,* James G. Williams,† Dale H. Boggs,† Ryan S. Park,* and Petr Kuchynka* ABSTRACT. — The planetary and lunar ephemerides DE430 and DE431 are generated by fitting numerically integrated orbits of the Moon and planets to observations. The present-day lunar orbit is known to submeter accuracy through fitting lunar laser ranging data with an updated lunar gravity field from the Gravity Recovery and Interior Laboratory (GRAIL) mission. The orbits of the inner planets are known to subkilometer accuracy through fitting radio tracking measurements of spacecraft in orbit about them. Very long baseline interfer- ometry measurements of spacecraft at Mars allow the orientation of the ephemeris to be tied to the International Celestial Reference Frame with an accuracy of 0′′.0002. This orien- tation is the limiting error source for the orbits of the terrestrial planets, and corresponds to orbit uncertainties of a few hundred meters. The orbits of Jupiter and Saturn are determined to accuracies of tens of kilometers as a result of fitting spacecraft tracking data. The orbits of Uranus, Neptune, and Pluto are determined primarily from astrometric observations, for which measurement uncertainties due to the Earth’s atmosphere, combined with star catalog uncertainties, limit position accuracies to several thousand kilometers. DE430 and DE431 differ in their integrated time span and lunar dynamical modeling. The dynamical model for DE430 included a damping term between the Moon’s liquid core and solid man- tle that gives the best fit to lunar laser ranging data but that is not suitable for backward integration of more than a few centuries.
    [Show full text]
  • Multi-Messenger Observations of a Binary Neutron Star Merger
    The Astrophysical Journal Letters, 848:L12 (59pp), 2017 October 20 https://doi.org/10.3847/2041-8213/aa91c9 © 2017. The American Astronomical Society. All rights reserved. Multi-messenger Observations of a Binary Neutron Star Merger LIGO Scientific Collaboration and Virgo Collaboration, Fermi GBM, INTEGRAL, IceCube Collaboration, AstroSat Cadmium Zinc Telluride Imager Team, IPN Collaboration, The Insight-Hxmt Collaboration, ANTARES Collaboration, The Swift Collaboration, AGILE Team, The 1M2H Team, The Dark Energy Camera GW-EM Collaboration and the DES Collaboration, The DLT40 Collaboration, GRAWITA: GRAvitational Wave Inaf TeAm, The Fermi Large Area Telescope Collaboration, ATCA: Australia Telescope Compact Array, ASKAP: Australian SKA Pathfinder, Las Cumbres Observatory Group, OzGrav, DWF (Deeper, Wider, Faster Program),AST3, and CAASTRO Collaborations, The VINROUGE Collaboration, MASTER Collaboration, J-GEM, GROWTH, JAGWAR, Caltech- NRAO, TTU-NRAO, and NuSTAR Collaborations,Pan-STARRS,TheMAXITeam,TZACConsortium, KU Collaboration, Nordic Optical Telescope, ePESSTO, GROND, Texas Tech University, SALT Group, TOROS: Transient Robotic Observatory of the South Collaboration, The BOOTES Collaboration, MWA: Murchison Widefield Array, The CALET Collaboration, IKI-GW Follow-up Collaboration, H.E.S.S. Collaboration, LOFAR Collaboration, LWA: Long Wavelength Array, HAWC Collaboration, The Pierre Auger Collaboration, ALMA Collaboration, Euro VLBI Team, Pi of the Sky Collaboration, The Chandra Team at McGill University, DFN: Desert Fireball Network, ATLAS, High Time Resolution Universe Survey, RIMAS and RATIR, and SKA South Africa/MeerKAT (See the end matter for the full list of authors.) Received 2017 October 3; revised 2017 October 6; accepted 2017 October 6; published 2017 October 16 Abstract On 2017 August 17 a binary neutron star coalescence candidate (later designated GW170817) with merger time 12:41:04 UTC was observed through gravitational waves by the Advanced LIGO and Advanced Virgo detectors.
    [Show full text]